Муниципальное бюджетное общеобразовательное учреждение
Лицей №2 Купинского района
Исследовательский проект
Тема:
«Построение сечения многогранников»
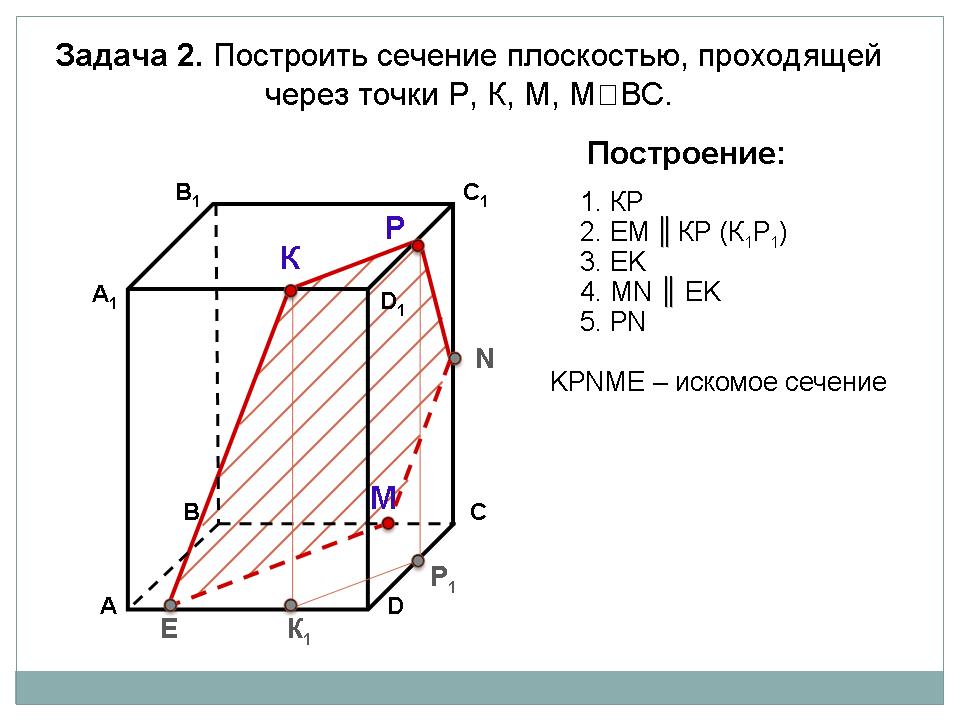
Работу выполнила:
ученица 10 «А» класса
МБОУ Лицея №2
Волковски Адриана Георгиевна
Руководитель проекта:
Иванова Елена Петровна
учитель математики
МБОУ Лицея №2
2022-2023г.
г.Купино
Содержание
1. Введение………………………………………………………………3 - 4
2. Основная часть
2.1 Обзор литературных и интернет источников…………………….....5
2.2 Методы построения сечений………………………………………6-12
3. Заключение……………………………………………………………...13
4. Список использованной литературы………………………………….14
5. Приложения………………………………………………………….. 15-21
6. Памятка для построения сечений……………………………………22
Введение
Изучением методов построения сечений занимается раздел математики - стереометрия. Построение сечений - один из важных блоков школьной программы. Главной проблемой является то, что не все ученики могут с легкостью видеть в пространстве, что приводит к затруднениям во время решения стереометрических задач. Примером такой задачи является номером 13 из ЕГЭ. Для многих учеников будет актуальным научится строить и описывать сечения и об этом говорит процент выполнения этого задания в нашем районе за прошлый год, который составил 0%. Одной из частей задачи зачастую является построение сечения и дальнейшая работа с ним.
Наиболее популярным методом построения является «Метод следов», так как он изучается в школьном курсе и является более легким. Но он не всегда удобен. В таком случае можно использовать второй метод - «Метод внутреннего проектирования». Комбинируя два этих способа можно, с большей вероятностью выполнить как минимум половину задачи. Так же важно уметь правильно описать построение сечения. Таким образом, умение учеников использовать два вида методов построения сечения и умение описывать их повысит процент выполнения данного задания.
Цель:
Исследовать методы построения сечений, применить для решения задач и составить памятку для учащихся 10-11классов.
Гипотеза:
Предполагаю, что наличие знаний о методах построения сечений позволяет быстрее и легче решать стереометрические задачи.
Задачи:
1) Изучить теоретический материал по данной теме.
2) Систематизировать методы решения задач на построение сечений.
3) Привести примеры задач на применение каждого метода.
Объект исследования: геометрия
Предмет исследования: сечение многогранников.
Методы исследования:
- анализ, синтез и структурирование полученной информации;
Целевая аудитория: люди любого возраста
Основная часть
2.1 Обзор литературных и интернет источников
1.1 Многогранник - это пространственное тело, ограниченное плоскими многоугольниками.
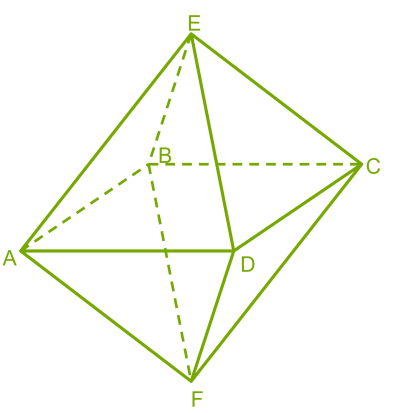

Плоские многоугольники называют гранями многогранника, (ECD); (DCF); (ADF); (ABF); (BCF); (BCE); (EBA); (AED) - грани; их вершины - вершинами многогранника- A; F; D; C; B; E; а стороны - ребрами многогранника- FA; FD; FC; FB; ED; EC; EB; EA;
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю многогранника- AC; BD;
1.2 Сечение многогранника — геометрическая фигура, образованная пересечением плоскости с многогранником. Сечением многогранника является многоугольник, вершины которого лежат на рёбрах, а стороны целиком на гранях многогранника.
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия.
2.2 Методы построения сечений
Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника. Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани.
Правила построения сечения:
Можно соединять только те точки, которые лежат в одной плоскости.
Если точки сечения лежат на ребрах с общей вершиной, то в сечении треугольник.
Для параллельной плоскости используется параллельный перенос.
Для нахождения точки пересечения ребра и плоскости сечения, продолжить можно только прямые лежащие на одной плоскости.
То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания.
Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.
Пример задачи:
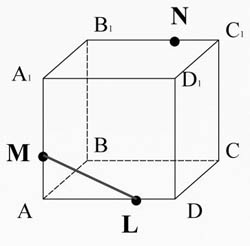
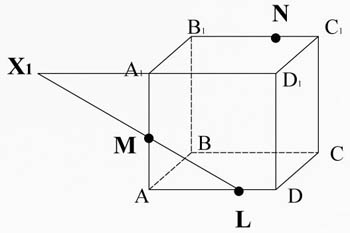
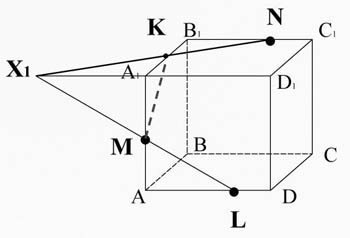
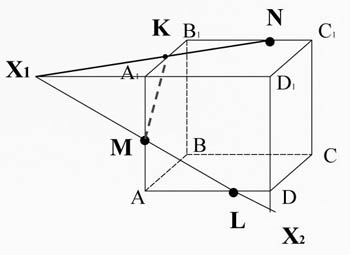
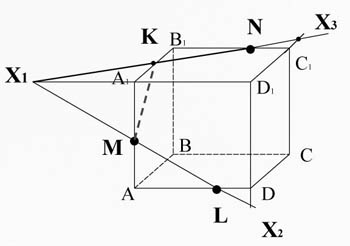
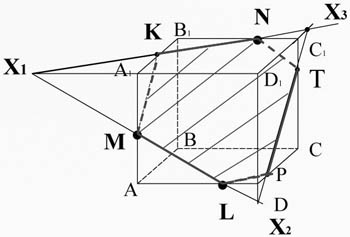
Постройте сечение куба ABCDA1B1C1D1 через заданные точки.
Дано: T∈BB1; K∈AA1; M∈CC1.
Построить: сечение 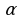
M∈(ADD1), L∈(ADD1) ⇒ ML⊂ (ADD1); LM∈(ADD1), D1A1∈(ADD1) ⇒ LM∩D1A1=X1; X1∈(A1D1C1), N∈(A1D1C1) ⇒ X1N⊂ (A1D1C1). A1B1∩X1N=K. K∈(A1AB), M∈(A1AB) =MK⊂ (A1AB). ML⊂(ADD1), DD1⊂(ADD1) ⇒ML∩DD1=X2; KN⊂(A1D1C1), D1C1⊂(A1D1C1) ⇒KN∩D1C1=X3. X2∈(DCC1), X3∈(DCC1) ⇒X2X3⊂(DCC1). X2X3⊂(DCC1), DC⊂(DCC1) ⇒X2X3∩DC=P. X2X3⊂(DCC1), CC1⊂(DCC1) ⇒ X2X3∩CC1=T. T∈(DCC1), P∈(DCC1) ⇒TP⊂(DCC1); N∈(BCC1), T∈(BCC1) ⇒ NT⊂(BCC1); L∈(ADC), P∈(ADC) ⇒ LP⊂(ADC). MKNTPL- искомое сечение.
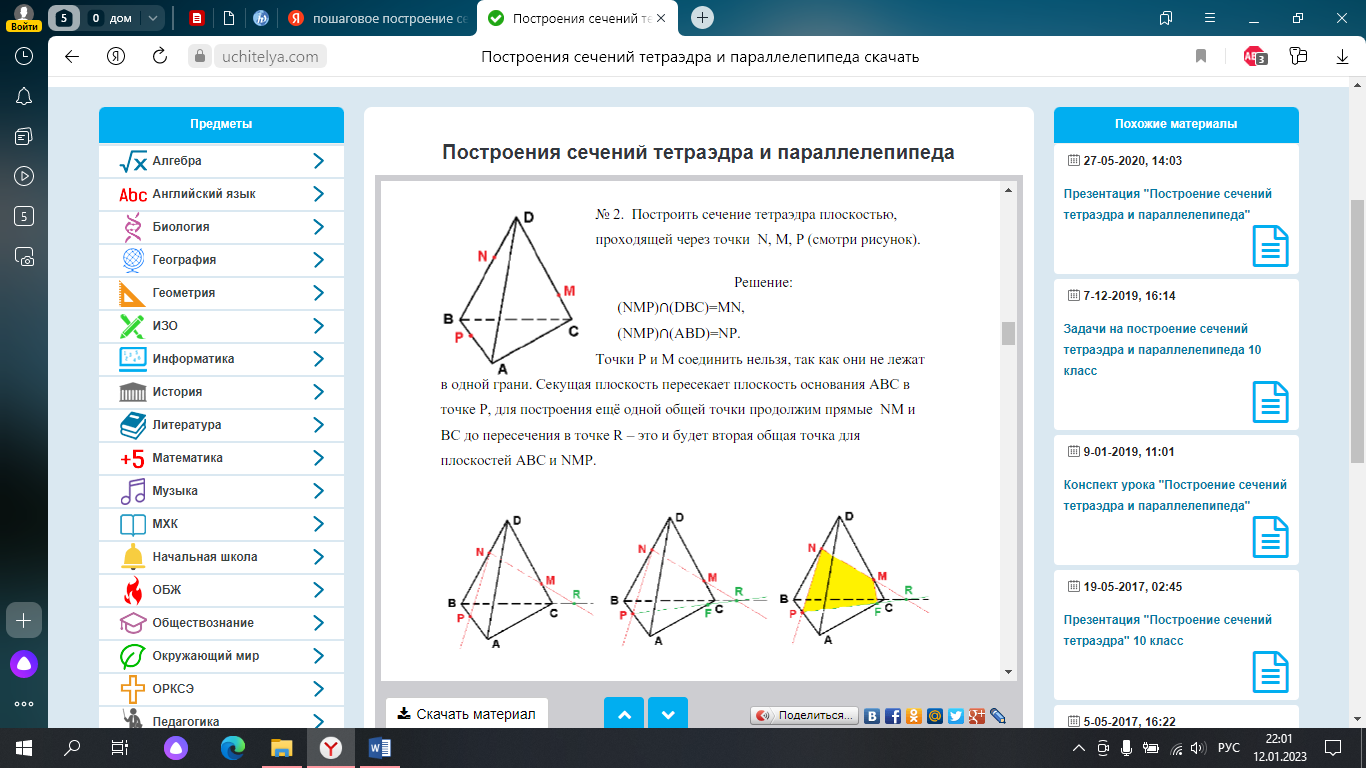
Пример задачи: Постройте сечение тетраэдра ABCD через заданные точки.
Дано: N∈BD; P∈BA; M∈CD.
Построить: сечение 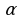
P∈(BAD), N∈(BAD) ⇒PN ⊂ (BAD); N∈(BCD), M∈(BCD) ⇒ NM⊂(BCD); NM∩AC=R. P∈(BAC), R∈(BAC) ⇒ PR⊂(BAC); PR∩AC=F. M∈(ADC) F∈(ADC) ⇒ MF⊂(ADC). FMNP-искомое сечение


Пример задачи: Построить сечение треугольной призмы ABCA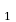 B
B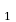 C
C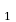 плоскостью, проходящей через заданные точки.
плоскостью, проходящей через заданные точки.
Дано: M∈A1C1; N∈CC1; K∈AB.
Построить: сечение 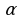
M∈(ACC1), N∈(ACC1) ⇒ MN⊂ (ACC1). NM∩AA1=O. O∈(ABB1), K∈(ABB1) ⇒ OK⊂(ABB1). OK∩A1B1=T. T∈(ABB1), K∈(ABB1) ⇒ TK⊂(ABB1). (A1B1C1) ∥ (ABC) ⇒ TM ∥α. α∩ BC=F. F∈(ABC), K∈(ABC) ⇒FK⊂(ABC). N∈(BCC1), F∈(BCC1) ⇒ NF⊂(BCC1). KFNMT- искомое сечение.
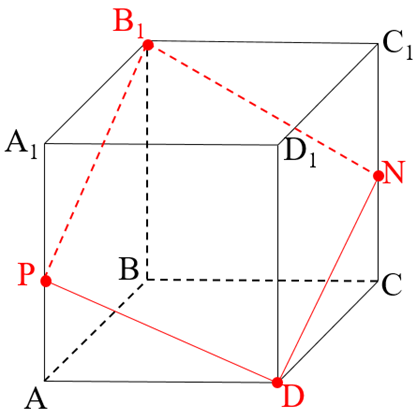
Пример задачи: В прямоугольном параллелепипеде ABCDA1B1C1D1 точка P лежит на ребре AA1, причём A1P : PA = 3 : 4, BB1 = 14, AD = 6. Плоскость DPB1 пересекает ребро CC1 в точке N, тангенс угла между прямой NP и плоскостью основания ABCD равен
а) Докажите, что четырехугольник DPB1N — ромб.
б) Найдите площадь сечения DPB1N.
Дано: P∈AA1; N∈CC1; D∈DD1; B1∈BB1.
Построить: сечение 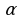
B1∈(ABB1), P∈(ABB1) ⇒ PB1 ⊂(ABB1). P∈(ADD1), D∈(ADD1) ⇒PD⊂(ADD1), D∈(DCC1), N∈(DCC1) ⇒ DN⊂(DCC1). B1∈(BCC1), N∈ (BCC1) ⇒ NB1⊂(BCC1). PDNB1-искомое сечение
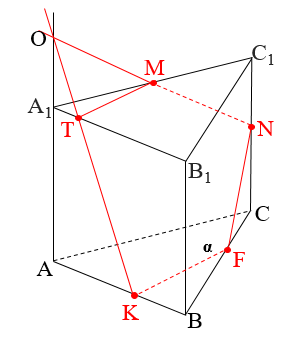
Метод внутреннего проектирования называют еще методом соответствий, или методом диагональных сечений.
При применении этого метода каждая заданная точка проектируется на плоскость основания. Существует два возможных вида проектирования: центральное и параллельное. Центральное проектирование, как правило, используется при построении сечений пирамид, вершина пирамиды при этом является центром проекции. Параллельное проектирование используется при построении сечений призм.
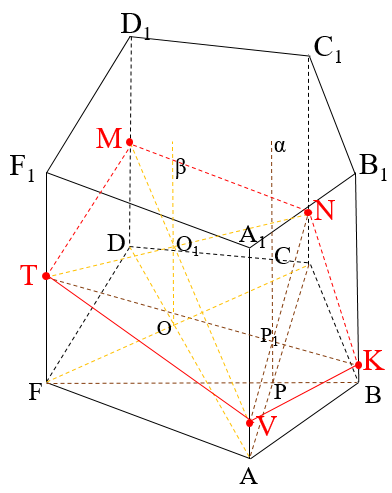
Пример задачи: Постройте сечение пятиугольной призмы ABCDFA1B1C1D1F1 через заданные точки.
Дано: T∈FF1; N∈CC1; K∈BB1.
Построить: сечение 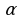
В четырехугольнике ABCF проведем диагонали AC и BF. AC∩BF = P, построим α∥AA1. T∈(FBB1), K∈(FBB1) ⇒TK⊂(FBB1). TK∩ α=P1. N∈(ACC1), P1∈(ACC1) ⇒ NP1⊂(ACC1). AA1⊂ (ACC1), NP1∩AA1=V. В четырехугольнике AFDC проведем диагонали DA и FC. DA∩FC=O, построим β∥AA1. T∈(FCC1), N∈(FCC1) ⇒TN⊂ (FCC1). TN∩β=O1. V∈ (ADD1), O1∈(ADD1) ⇒VO1⊂(ADD1), DD1⊂ (ADD1). VO1∩DD1=M. N∈(BCC1), K∈(BCC1) ⇒NK⊂(BCC1), B∈(ABB1), V∈(ABB1) ⇒BV⊂(ABB1), V∈(FAA1), T∈(FAA1) ⇒VT⊂ (FAA1), T∈(DFF1), M∈(DFF1) ⇒TM⊂(DFF1), M∈(DCC1), N∈(DCC1) ⇒MN⊂(DCC1). VTMNK-искомое сечение.
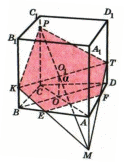
Пример задачи: Постройте сечение куба ABCDA1B1C1D1 через заданные точки.
Дано: T∈DD1; P∈CC1; K∈BB1.
Построить: сечение 
T∈(CDD1), P∈(CDD1) ⇒TP⊂(CDD1). P∈(BCC1), K∈(BCC1) ⇒PK⊂(DCC1). В четырехугольнике ABCD проведем диагонали AC и BD. AC∩BD=O. Построим α∥AA1. K∈(BDD1), T∈(BDD1) ⇒KT⊂(BDD1). KT∩ α=O1. P∈(CAA1), O1∈(CAA1) ⇒PO1⊂ (CAA1). AA1⊂ (CAA1). PO1∩AA1=M. K∈(BAA1), M∈(BAA1) ⇒KM⊂(BAA1), KM∩BA=E. T∈(ADD1), M∈(ADD1) ⇒TM⊂(ADD1). TM∩AD=F. E∈(ABC), F∈(ABC) ⇒ EF⊂(ABC). FEPKE-искомое сечение.
Пример задачи: В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SЕ и вершину С, делит ребро SВ в отношении 1: 3, считая от вершины В.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SА и SЕ и вершину С, делит ребро SF, считая от вершины S.
Дано: M∈CS; H∈SD; K∈BS.
Построить: сечение 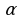
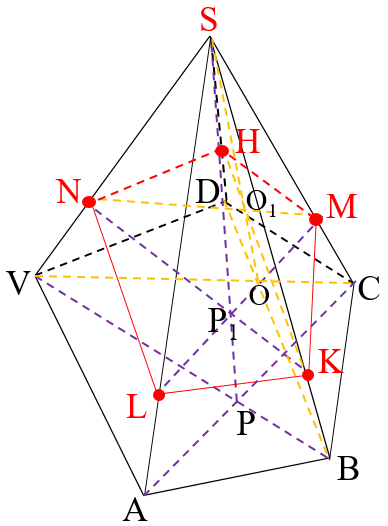 В четырехугольнике ABCV. Проведем диагонали AC и BV. AC∩BV=P. Построим PS. N∈(VBS), K∈(VBS) ⇒NK⊂(VBS). NK∩PS=P1. M∈(ACS), P1∈(ACS) ⇒MP1⊂(ACS).AS⊂(ACS), MP1∩AS=L. В четырехугольнике BCDV. Проведем диагонали VC и DB. VC∩DB=O. Проведем OS. H∈(DBS), K∈(DBS) ⇒HK⊂(DBS). HK∩OS=O1. M∈(VCS), O1∈(VCS) ⇒MO1⊂(VCS). VS⊂(VCS). MO1∩VS=N. L∈(ABS), K∈(ABS)⇒LK⊂(ABS), K∈(BCS), M∈(BCS)⇒KM⊂(BCS), M∈(DCS), H∈(DCS)⇒MH⊂(DCS), H∈(VDS), N∈(VDS) ⇒HN⊂(VDS), N∈(VAS), L∈(VAS) ⇒NL⊂(VAS). LKMHN-искомое сечение
В четырехугольнике ABCV. Проведем диагонали AC и BV. AC∩BV=P. Построим PS. N∈(VBS), K∈(VBS) ⇒NK⊂(VBS). NK∩PS=P1. M∈(ACS), P1∈(ACS) ⇒MP1⊂(ACS).AS⊂(ACS), MP1∩AS=L. В четырехугольнике BCDV. Проведем диагонали VC и DB. VC∩DB=O. Проведем OS. H∈(DBS), K∈(DBS) ⇒HK⊂(DBS). HK∩OS=O1. M∈(VCS), O1∈(VCS) ⇒MO1⊂(VCS). VS⊂(VCS). MO1∩VS=N. L∈(ABS), K∈(ABS)⇒LK⊂(ABS), K∈(BCS), M∈(BCS)⇒KM⊂(BCS), M∈(DCS), H∈(DCS)⇒MH⊂(DCS), H∈(VDS), N∈(VDS) ⇒HN⊂(VDS), N∈(VAS), L∈(VAS) ⇒NL⊂(VAS). LKMHN-искомое сечение
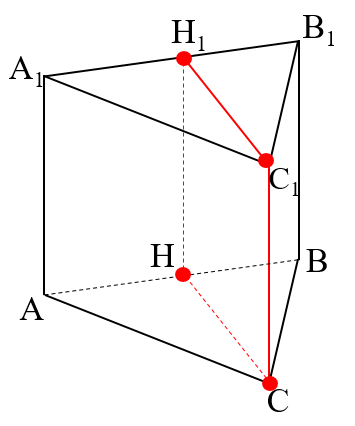
Пример задачи: В прямой треугольной призме стороны основания равна 10, 17 и 21, а высота 18. Найдите площадь сечения, веденного через боковое ребро и меньшую высоту основания.
Дано: ABCA1B1C1- прямая призма. AA1=18, AC=17, CB=10, AB=21. 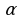 -сечение.
-сечение.
Найти: S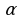
Меньшая h в треугольнике проводится к большей стороне ⇒ CH- искомая высота. CH∥C1H1, CH=C1H1 так как (ACB)∥(A1C1B1). H∈(ABB1), H1∈(ABB1) ⇒ HH1⊂(ABB1). CC1HH1- искомое сечение 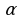 , значит CC1HH1 параллелограмм. CC1 ⊥ (ABC), CH⊂(ABC) ⇒CC1⊥CH⇒∠CC1H=90°⇒ CHH1C1- прямоугольник. SCHH1C1=CC1×CH. S△ABC =
, значит CC1HH1 параллелограмм. CC1 ⊥ (ABC), CH⊂(ABC) ⇒CC1⊥CH⇒∠CC1H=90°⇒ CHH1C1- прямоугольник. SCHH1C1=CC1×CH. S△ABC = 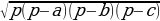 , p=
, p=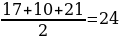 , S△=
, S△=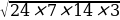 =
= 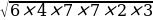 =2×7×6=84. S=
=2×7×6=84. S=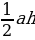 , S=
, S=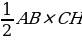 , 84=
, 84=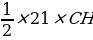 , CH=
, CH=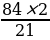 =8. SCHH1C1=18×8=144
=8. SCHH1C1=18×8=144
Ответ: 144
Заключение
Работая над проектом, я исследовала методы построения сечений. В ходе решения практических задач применила оба способа и смогла сделать вывод, что при подготовке к ЕГЭ нужно научиться использовать и тот и другой методы построения сечений. Метод следов является менее сложным, нежели метод внутренней проекции, но при этом в них можно разобраться и в дальнейшем комбинировать для более быстрого решения задач.
А также я научилась использовать эти способы для решения задач и правильно оформлять само построение. Для меня способ внутреннего проектирования показался более универсальным и подходящим почти под все задачи, но несмотря на это данный способ является довольно сложным. Ученикам мой проект поможет разобраться какой из способов подойдет именно им, а также научит правильно описывать построение сечений.
После ознакомления с информацией моего проекта, предлагаю список задач в приложении, которые помогут закрепить полученные теоретические знания и подойдут для подготовки к егэ. А так же я составила памятку для пострения сечений.
Литературные источники
https://www.sites.google.com/site/polyhedrasection2014/postroenie-secenij/sloznye-secenia-metod-sledov
https://studopedia.ru/25_38917_metod-vnutrennego-proektirovaniya.html
Геометрия. 10 класс. Задачник. Углубленный уровень - Потоскуев Е.В., Звавич Л.И.
Геометрия. 10 класс. Учебник. Углубленный уровень - Потоскуев Е.В., Звавич Л.И.
Геометрия. 11 класс. Задачник. Углубленный уровень - Потоскуев Е.В., Звавич Л.И.
Геометрия. 11 класс. Учебник. Углубленный уровень - Потоскуев Е.В., Звавич Л.И.
Литвиненко В.Н практикум по решению задач школьной математики, геометрия
Приложение
1. В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
3. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — середина ребра B1C1. Известно, что  AD = 12, AA1 = 14.
AD = 12, AA1 = 14.
а) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4 : 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
4. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T − середина ребра B1C1. Известно, что  AD = 10, AA1 = 16.
AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
5. Основанием прямой четырехугольной призмы ABCDA'B'C'D' является квадрат ABCD со стороной  высота призмы равна
высота призмы равна  Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 13. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.
б) Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью α.
7. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 9.
Основание O высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра SB , точка L лежит на ребре CD так, что CL : LD = 7 : 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S1LM — равнобедренная трапеция.
б) Вычислите длину средней линии этой трапеции.
8. Дана правильная призма ABCA1B1C1, у которой сторона основания AB = 4, а боковое ребро AA1 = 9. Точка M — середина ребра AC, а на ребре AA1 взята точка T так, что AT = 5.
а) Докажите, что плоскость BB1M делит отрезок C1T пополам.
б) Плоскость BTC1 делит отрезок MB1 на две части. Найдите длину меньшей из них.
9. Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
10. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64.
а) Постройте прямую пересечения плоскости SAC и плоскости, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания.
б) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирамиды плоскостью SAC равна 64.
11. Все рёбра правильной четырёхугольной пирамиды SABCD с вершиной S равны 6. Основание высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра AS, точка L лежит на ребре BC так, что BL : LC = 1 : 2.
а) Докажите, что сечение пирамиды SABCD плоскостью S1LM — равнобокая трапеция.
б) Вычислите длину средней линии этой трапеции.
12. В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро  На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
13. В правильной четырехугольной призме ABCDA1B1C1D1 точка K делит боковое ребро AA1 в отношении AK : KA1 = 1 : 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD1 в точке M.
а) Докажите, что плоскость α делит ребро DD1 в отношении DM : MD1 = 2 : 1.
б) Найдите площадь сечения, если известно, что AB = 4, AA1 = 6.
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 4, BC = 3, AA1 = 2. Точки P и Q — середины рёбер A1B1 и CC1 соответственно. Плоскость APQ пересекает ребро B1C1 в точке U.
а) Докажите, что B1U : UC1 = 2 : 1.
б) Найдите площадь сечения параллелепипеда ABCDA1B1C1D1 плоскостью APQ.
15. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 5, а боковые рёбра равны 11.
а) Докажите, что прямые CA1 и C1D1 перпендикулярны.
б) Найдите площадь сечения призмы плоскостью, проходящей через вершины C, A1 и F1.
16. Точки P и Q — середины рёбер AD и CC1 куба ABCDA1B1C1D1 соответственно.
а) Докажите, что прямые B1P и QB перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 10.
17. Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M.
а) Докажите, что MD : MD1 = 2 : 1.
б) Найдите площадь сечения, если AB = 4, AA1 = 6.
18. Дана правильная четырёхугольная пирамида MABCD, все рёбра которой равны 12. Точка N — середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2 : 1, считая от вершины M.
а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
19. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
20. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ : QB = 1 : 2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
21. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ : QB = 1 : 2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 
22. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MC.
а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограммом.
б) Найдите площадь сечения пирамиды MABC плоскостью α.
23. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 4. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MС.
а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограммом.
б) Найдите площадь сечения пирамиды MABC плоскостью α.
24. В правильной треугольной пирамиде MABC боковые рёбра равны 10, а сторона основания равна 12. Точки G и F делят стороны основания AB и AC соответственно так, что AG : GB = AF : FC = 1 : 5.
а) Докажите, что сечение пирамиды плоскостью MGF является равнобедренным треугольником.
б) Найдите площадь сечения пирамиды плоскостью MGF.
25. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD. Противоположные боковые грани пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MC.
а) Докажите, что плоскость α параллельна ребру MD.
б) Найдите угол между плоскостью α и прямой AC.
26. Через середину бокового ребра правильной треугольной пирамиды проведена плоскость α, перпендикулярная этому ребру. Известно, что она пересекает остальные боковые рёбра и разбивает пирамиду на два многогранника, объёмы которых относятся как 1 : 3.
а) Докажите, что плоский угол при вершине пирамиды равен 45°.
б) Найдите площадь сечения пирамиды плоскостью α, если боковое ребро пирамиды равно 4.
27. В основании пирамиды DABC лежит прямоугольный треугольник ABC с катетами AC = 15 и BC = 9. Точка M — середина ребра AD. На ребре BC выбрана точка E так, что CE = 3, а на ребре AC выбрана точка F так, что CF = 5. Плоскость MEF пересекает ребро BD в точке N. Расстояние от точки M до прямой EF равно 
а) Докажите, что N — середина ребра BD.
б) Найдите площадь сечения пирамиды плоскостью MNF.
28. В правильном тетраэдре ABCD точки K и M — середины рёбер AB и CD соответственно. Плоскость α содержит прямую KM и параллельна прямой AD.
а) Докажите, что сечение тетраэдра плоскостью α — квадрат.
б) Найдите площадь сечения тетраэдра ABCD плоскостью α, если 
29. В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 5. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC = 5 : 1. Плоскость α содержит прямую KM и параллельна SA.
а) Докажите, что сечение пирамиды SABC плоскостью α — прямоугольник.
б) Найдите объём пирамиды, вершиной которой является точка A, а основанием — сечение пирамиды SABC плоскостью α.
30. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 9. Основание O высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра SB, точка L лежит на ребре CD так, что CL : LD = 7 : 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S1LM — равнобедренная трапеция.
б) Вычислите длину средней линии этой трапеции.
31. В прямоугольном параллелепипеде ABCDA1B1C1D1 через диагональ BD1 проведена плоскость α, параллельная прямой AC.
а) Докажите, что прямая пересечения плоскости α с плоскостью основания A1B1C1D1 параллельна прямой A1C1.
б) Найдите угол между проведённой плоскостью и плоскостью основания параллелепипеда, если AB = 6, BC = 8, CC1 = 10.
32. Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р — середина А1D1, точка Q делит отрезок АВ1 в отношении 2 : 1, считая от вершины А, R — точка пересечения отрезков ВС1 и В1С.
а) Найдите площадь сечения куба плоскостью PQR.
б) Найдите отношение, в котором плоскость сечения делит диагональ АС1 куба.
33. Дана прямая треугольная призма ABCA1B1C1. Известно, что AB = BC. Точка K — середина ребра A1B1, а точка M лежит на ребре AC и делит его в отношении AM : MC = 1 : 3.
а) Докажите, что прямая KM перпендикулярна прямой AC .
б) Найдите расстояние между прямыми KM и A1C1, если AB = 10, AC = 8 и AA1 = 3.
34. В правильной шестиугольной пирамиде SABCDEF боковое ребро SA = 14, а сторона AB = 8. Точка М середина стороны AB Плоскость α проходит через точки M и D и перпендикулярна плоскости ABC. Прямая SC пересекает плоскость α в точке K.
a) Докажите, что MK = KD.
б) Найдите объем пирамиды MCDK.
35. Дана правильная треугольная пирамида SABC в которой AB = 9, точка M лежит на ребре AB так, что AM = 8. Точка K делит сторону SB так, что SK : KB = 7 : 3. Ребро  Точки M и K принадлежат плоскости α, которая перпендикулярна плоскости ABC.
Точки M и K принадлежат плоскости α, которая перпендикулярна плоскости ABC.
а) Докажите, что точка С принадлежит плоскости α.
б) Найдите площадь сечения α.
36. Дана правильная треугольная пирамида SABC в которой AB = 6, точка M лежит на ребре AB так, что AM = 5. Точка K делит сторону SB так, что SK : KB = 4 : 3. Ребро  Точки M и K принадлежат плоскости α, которая перпендикулярна плоскости ABC.
Точки M и K принадлежат плоскости α, которая перпендикулярна плоскости ABC.
а) Докажите, что точка С принадлежит плоскости α.
б) Найдите площадь сечения α.
37. Дана правильная треугольная призма ABCA1B1C1, в которой сторона основания AB = 8, боковое ребро  Точка Q — точка пересечения диагоналей грани ABB1А1, точки M, N и K — середины ВС, СC1 и А1C1 cответственно.
Точка Q — точка пересечения диагоналей грани ABB1А1, точки M, N и K — середины ВС, СC1 и А1C1 cответственно.
а) Докажите, что точки Q, M, N и K лежат в одной плоскости.
б) Найдите площадь сечения QMN.
38. В правильной четырехугольной пирамиде SABCD с вершиной S стороны основания равны 18, а боковые ребра 15. Точка R принадлежит ребру SB, причем SR : RB = 2 : 1.
а) Докажите, что плоскость, проходящая через точки С и R параллельно BD делит ребро SA пополам.
б) Найдите площадь сечения пирамиды этой плоскостью.
39. В основании четырехугольной пирамиды SАВСD лежит параллелограмм АВСD c центром О. Точка N — середина ребра SC, точка L — середина ребра SA.
а) Докажите, что плоскость BNL делит ребро SD в отношении 1 : 2, считая от вершины S.
б) Найдите угол между плоскостями BNL и АВС, если пирамида правильная, SA = 8, а тангенс угла между боковым ребром и плоскостью основания пирамиды равен 
40. В правильной четырехугольной пирамиде MABCD через середины сторон АВ и AD параллельно боковому ребру АМ проведена плоскость. Сторона основания пирамиды равна 20, а боковое ребро — 
а) Докажите, что сечение пирамиды этой плоскостью является пятиугольником с тремя прямыми углами.
б) Найдите площадь этого сечения.
41. В четырёхугольной пирамиде SABCD все рёбра равны 6, точка M — середина отрезка AS.
а) Докажите, что прямая AS перпендикулярна плоскости BMD.
б) Найдите площадь сечения пирамиды плоскостью BMD.
42. В правильной четырёхугольной пирамиде FABCD с вершиной F сторона основания равна  боковое ребро равно 15. Точка N делит высоту пирамиды в отношении 2 : 1, считая от вершины F. Через точки B и N параллельно прямой AC проведена плоскость γ, пересекающая ребро DF в точке M.
боковое ребро равно 15. Точка N делит высоту пирамиды в отношении 2 : 1, считая от вершины F. Через точки B и N параллельно прямой AC проведена плоскость γ, пересекающая ребро DF в точке M.
а) Докажите, что точка M — середина отрезка DF.
б) Найдите площадь сечения пирамиды плоскостью γ.
43. Плоскость α проходит через середины двух противоположных ребер треугольной пирамиды и параллельна медиане одной из ее граней.
а) Докажите, что среди медиан граней этой пирамиды в точности две являются параллельными к плоскости α.
б) Найдите площадь сечения данной пирамиды плоскостью α, если эти медианы перпендикулярны друг другу и равны 2.
44. В правильной четырёхугольной пирамиде SABCD боковое ребро SA равно 12, а сторона основания AB равна 6. В боковых гранях SAB и SAD провели биссектрисы AL и AM соответственно.
а) Докажите, что сечение пирамиды плоскостью ALM делит ребро SC пополам.
б) Найдите площадь сечения пирамиды плоскостью ALM.
45. В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = 2, SK = 1. Плоскость  перпендикулярна плоскости ABC и содержит точки M и K.
перпендикулярна плоскости ABC и содержит точки M и K.
а) Докажите, что плоскость  содержит точку C.
содержит точку C.
б) Найдите площадь сечения пирамиды SABCD плоскостью 
46. В правильной восьмиугольной призме ABCDEFGHA1B1C1D1E1F1G1H1 сторона основания AB равна  а боковое ребро AA1 равно 6. Ha pe6pe CC1 отмечена точка M так, что
а боковое ребро AA1 равно 6. Ha pe6pe CC1 отмечена точка M так, что  Плоскость
Плоскость  параллельна прямой H1E1 и проходит через точки M и A.
параллельна прямой H1E1 и проходит через точки M и A.
а) Докажите, что сечение данной призмы плоскостью α — равнобедренная трапеция.
б) Найдите объем пирамиды, вершиной которой является точка F1, а основанием — сечение данной призмы плоскостью α.
47. В прямоугольном параллелепипеде ABCDA1B1C1D1 точка P лежит на ребре AA1, причём A1P : PA = 3 : 4, BB1 = 14, AD = 6. Плоскость DPB1 пересекает ребро CC1 в точке N, тангенс угла между прямой NP и плоскостью основания ABCD равен 
а) Докажите, что четырехугольник DPB1N — ромб.
б) Найдите площадь сечения DPB1N.
48. В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно  На ребрах AB и SB отмечены точки M и K соответственно, причем AM = 4, SK : KB = 1 : 3.
На ребрах AB и SB отмечены точки M и K соответственно, причем AM = 4, SK : KB = 1 : 3.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
49. Точка E лежит на высоте SO, а точка F — на боковом ребре SC правильной четырёхугольной пирамиды SABCD, причём SE : EO = SF : FC = 2 : 1.
а) Докажите, что плоскость BEF пересекает ребро SD в его середине.
б) Найдите площадь сечения пирамиды плоскостью BEF, если AB = 8, SO = 14.
50. В правильном тетраэдре SABC точка M — середина ребра AB, а точка N расположена на ребре SC так, что SN : NC = 3 : 1.
а) Докажите, что плоскости SMC и ANB перпендикулярны.
б) Найдите длину отрезка MN, если длина ребра AB равна 8.
51. В прямоугольном параллелепипеде ABCDA1B1C1D1 проведена секущая плоскость, содержащая диагональ AC1 и пересекающая ребра BB1 и DD1 в точках F и E соответственно.
а) Докажите, что сечение AFC1E — параллелограмм.
б) Найдите площадь сечения, если известно, что AFC1E — ромб и AB = 3, BC = 2, AA1 = 5.
52. Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре BB1 отмечена точка Q такая, что BQ : QB1 = 2 : 7. Плоскость α проходит через точки A и Q параллельно прямой BD. Эта плоскость пересекает ребро CC1 в точке M.
а) Докажите, что C1M : CC1 = 5 : 9.
б) Найдите площадь сечения, если  AA1 = 18.
AA1 = 18.
53. Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K — середина AS. Плоскость, проходящая через точку K и параллельная основанию пирамиды, пересекает ребра SB и SC в точках Q и P соответственно.
а) Докажите, что площадь PQBС относится к площади как 3 : 4.
как 3 : 4.
б) Найдите объем пирамиды KBQPC.
54. В прямоугольном параллелепипеде ABCDA1B1C1D1 проведена секущая плоскость, содержащая диагональ AC1 и пересекающая ребра BB1 и DD1 в точках F и E соответственно.
а) Докажите, что сечение AFC1E — параллелограмм.
б) Найдите площадь сечения, если известно, что AFC1E — ромб и AB = 3, BC = 2, AA1 = 5.
55. Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N — середины рёбер AB и BC соответственно. Все ребра пирамид равны.
а) Докажите, что угол между прямыми AE и BF равен 60°.
б) Найдите угол между прямыми EM и FN.
56. В кубе ABCDA1B1C1D1 точки K, L и M — середины ребер AB, B1C1 и DD1.
а) Докажите, что сечение куба плоскостью KLM является правильным многоугольником.
б) Найдите расстояния от точки A до плоскости KLM, если ребро куба равно 2.
57. На ребре BB1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка F так, что B1F : FB = 1 : 6. Точка T — середина ребра B1C1. Известно, что  AD = 12, AA1 = 14.
AD = 12, AA1 = 14.
а) Докажите, что плоскость FTD1 делит ребро AA1 в отношении 2 : 5.
б) Найдите площадь сечения параллелепипеда плоскостью FTD1.
58. Точка E лежит на боковом ребре SC правильной четырехугольной пирамиды SABCD и делит его в отношении 1 : 2, считая от вершины S. Через точку E и середины сторон AB и AD проведена плоскость α.
а) Докажите, что плоскость α делит высоту пирамиды в отношении 3 : 2.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если сторона основания пирамиды равна 12, а высота — 
59. В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SЕ и вершину С, делит ребро SВ в отношении 1 : 3, считая от вершины В.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SА и SЕ и вершину С, делит ребро SF, считая от вершины S.
60. В правильной треугольной пирамиде SABC с вершиной S точки M и N — середины ребер AB и BC соответственно. Плоскость α проходит через точки M и N и пересекает ребра AS и CS в точках K и P соответственно.
а) Докажите, что точка пересечения прямых MP и KN лежит на высоте пирамиды SABC.
б) Найдите площадь сечения пирамиды SABC плоскостью α, если известно, что АВ = 24, AS = 28, SK = 7.
61. В правильной четырехугольной призме MNPQM1N1P1Q1 сторона основания равна 11, а боковое ребро — 15. На ребрах M1Q1, M1N1 и PQ взяты точки X, Y, Z соответственно так, что 
а) Пусть C — точка пересечения плоскости XYZ c ребром PN. Докажите, что XYCZ — прямоугольник.
б) Найдите площадь сечения призмы плоскостью XYZ.
62. В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N — середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если 

 а прямая SO перпендикулярна прямой AD.
а прямая SO перпендикулярна прямой AD.
63. Дана правильная четырёхугольная пирамида SABCD. Точка M — середина SA, на ребре SB отмечена точка N так, что 
а) Докажите, что плоскость CMN параллельна прямой SD.
б) Найдите площадь сечения пирамиды плоскостью CMN, если все рёбра равны 12.
64. SMNK — правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР : PS = 1 : 3, точка L — середина ребра MN.
а) Докажите, что плоскости SLK и MPN перпендикулярны.
б) Найдите длину отрезка PL, если длина ребра MN равна 4.
65. В правильной четырехугольной пирамиде SABCD точка L — середина бокового ребра SB. На ребре SA взята точка К так, что 
а) Докажите, что плоскость DKL параллельна боковому ребру SC.
б) Найдите площадь сечения пирамиды плоскостью DKL, если все ребра пирамиды равны 24.
66. В прямоугольном параллелепипеде ABCDA1B1C1D1 через середину M диагонали AC1 проведена плоскость α перпендикулярно этой диагонали, AB = 5, BC = 3 и AA1 = 4.
а) Докажите, что плоскость α содержит точку D1.
б) Найдите отношение, в котором плоскость  делит ребро A1B1.
делит ребро A1B1.
67. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 отмечена точка E так, что  точка T — середина ребра B1C1. Длины рёбер AD и A A1 равны 6 и 10 соответственно.
точка T — середина ребра B1C1. Длины рёбер AD и A A1 равны 6 и 10 соответственно.
a) Докажите, что сечение параллелепипеда плоскостью ETD1 является равнобедренной трапецией.
б) Найдите площадь сечения параллелепипеда ABCDA1B1C1D1 плоскостью ETD1, если 
Памятка для построения сечений
Сечение многогранника — геометрическая фигура, образованная пересечением плоскости с многогранником. Сечением многогранника является многоугольник, вершины которого лежат на рёбрах, а стороны целиком на гранях многогранника.
Методы построения сечений
Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника. Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани.
Правила построения сечения:
1. Можно соединять только те точки, которые лежат в одной плоскости.
2. Если точки сечения лежат на ребрах с общей вершиной, то в сечении треугольник.
3. Для параллельной плоскости используется параллельный перенос.
4. Для нахождения точки пересечения ребра и плоскости сечения, продолжить можно только прямые лежащие на одной плоскости.
То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания.
Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.
Метод внутреннего проектирования называют еще методом соответствий, или методом диагональных сечений.
При применении этого метода каждая заданная точка проектируется на плоскость основания. Существует два возможных вида проектирования: центральное и параллельное. Центральное проектирование, как правило, используется при построении сечений пирамид, вершина пирамиды при этом является центром проекции. Параллельное проектирование используется при построении сечений призм.










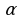










 B
B


 В четырехугольнике ABCV. Проведем диагонали AC и BV. AC∩BV=P. Построим PS. N∈(VBS), K∈(VBS) ⇒NK⊂(VBS). NK∩PS=P1. M∈(ACS), P1∈(ACS) ⇒MP1⊂(ACS).AS⊂(ACS), MP1∩AS=L. В четырехугольнике BCDV. Проведем диагонали VC и DB. VC∩DB=O. Проведем OS. H∈(DBS), K∈(DBS) ⇒HK⊂(DBS). HK∩OS=O1. M∈(VCS), O1∈(VCS) ⇒MO1⊂(VCS). VS⊂(VCS). MO1∩VS=N. L∈(ABS), K∈(ABS)⇒LK⊂(ABS), K∈(BCS), M∈(BCS)⇒KM⊂(BCS), M∈(DCS), H∈(DCS)⇒MH⊂(DCS), H∈(VDS), N∈(VDS) ⇒HN⊂(VDS), N∈(VAS), L∈(VAS) ⇒NL⊂(VAS). LKMHN-искомое сечение
В четырехугольнике ABCV. Проведем диагонали AC и BV. AC∩BV=P. Построим PS. N∈(VBS), K∈(VBS) ⇒NK⊂(VBS). NK∩PS=P1. M∈(ACS), P1∈(ACS) ⇒MP1⊂(ACS).AS⊂(ACS), MP1∩AS=L. В четырехугольнике BCDV. Проведем диагонали VC и DB. VC∩DB=O. Проведем OS. H∈(DBS), K∈(DBS) ⇒HK⊂(DBS). HK∩OS=O1. M∈(VCS), O1∈(VCS) ⇒MO1⊂(VCS). VS⊂(VCS). MO1∩VS=N. L∈(ABS), K∈(ABS)⇒LK⊂(ABS), K∈(BCS), M∈(BCS)⇒KM⊂(BCS), M∈(DCS), H∈(DCS)⇒MH⊂(DCS), H∈(VDS), N∈(VDS) ⇒HN⊂(VDS), N∈(VAS), L∈(VAS) ⇒NL⊂(VAS). LKMHN-искомое сечение
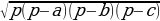 , p=
, p=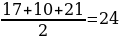 , S△=
, S△=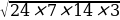 =
= 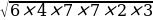 =2×7×6=84. S=
=2×7×6=84. S=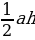 , S=
, S=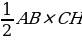 , 84=
, 84=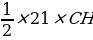 , CH=
, CH=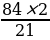 =8. SCHH1C1=18×8=144
=8. SCHH1C1=18×8=144 AD = 12, AA1 = 14.
AD = 12, AA1 = 14.










