Нестандартные способы решения квадратных уравнений
Содержание
Введение 3
Глава 1.Квадратные уравнения: из древности до наших дней 4
Глава 2. Тезаурус по теме.
2.1. Определение квадратного уравнения и его виды 8
2.2. Решение квадратного уравнения общеизвестными способами 9
Глава 3. Способы решения квадратных уравнений, отличные от традиционных
3.1. Метод выделения полного квадрата
3.2. Решения уравнений способом «переброски»................................................12
3.3. Учёт свойств коэффициентов квадратного уравнения………………….....13
3.4. Решение квадратного уравнения графическим способом………………...15
3.5. Решение квадратных уравнений с помощью циркуля и линейки………...16
3.6. Решение квадратных уравнений с помощью номограммы………………..18
3.7. Геометрический способ решения квадратных уравнений…………………19
3.8.Решение уравнений с использованием теоремы Безу……………................20
Глава 4.Разработка буклета памятки………………….…………………………..22
Заключение………………………………………………………………………….23
Литература…………………………………………………………………………..24
Нестандартные способы решения квадратных уравнений
Введение
Сегодня все пространство окружающее современного человека связано с математикой. А постоянные открытия в физике, технике и информационных технологиях говорят о том, что этот процесс постоянно растет. Поэтому решение многих практических задач сводится к различным уравнениям, и очень часто эти уравнения являются квадратными.
В школьном курсерассматривается несколько типов квадратных уравнений, и способы их решения по формулам. Вместе с тем, современные научно--методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Выбор способа должен оставаться за учащимися. Каждый ученик должен уметь верно и главное рационально решать квадратные уравнения. Так как в некоторых случаях можно решать их устно, только для этого необходимо помнить алгоритм решения квадратных уравнений, который может пригодиться во время экзаменов (ОГЭ и ЕГЭ, учитывая ограниченность экзамена во времени), при поступлении в ВУЗы и различных жизненных ситуациях.
Таким образом, возникает необходимость изучения этих дополнительных способов решения. Все сказанное выше определяет актуальность проблемы выполненной работы.
Цельюработы является выявление способов решения уравнений второй степени, отличных отизучаемых в школьной программе и оценка их с точки зрения удобства применения.
Задачи:
1)Познакомиться с историческими фактами, связанными с данным вопросом.
2)Описать технологии различных существующих способов решения уравнений второй степени.
3)Провести анализ этих способов, сравнить их.
4)Привести примеры применения различных способов решения уравнений.
5)Составить буклет-памятку со всеми изученными способами решения квадратных уравнений.
Объект исследования: уравнения второй степени.
Предмет исследования: способы решения уравнений второй степени.
ГЛАВА 1. Квадратные уравнения: из древности до наших дней
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000лет до нашей эры вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, как неполных, так и, полные квадратные уравнения. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VIIв.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме.В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XIIв. Бхаскары.
Обезьянок резвых стая
Власть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок
Ты скажи мне, в этой стае?
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т.е. ax2 + c =bx(5х2=10х).
«Квадраты равны числу», т. е. ax2=c(5x2=80).
«Корни равны числу», т. е. ax=c(4х=20).
«Квадраты и числа равны корням»,т.е.ax2+c=bx(х2+ 10х=39).
«Квадраты и корни равны числу», т. е. ax2+bx=c(x2+21=10x).
«Корни и числа равны квадратам», т. е. bx+c=ax2 (3х+4=х2).
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVIIв., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17вв. и частично 18.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2+bх=с, при всевозможных комбинациях знаков коэффициентовb, c , было сформулировано в Европе в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых вXVIв. учитывают, помимо положительных, и отрицательные корни. Лишь вXVIIв. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была сформулирована им впервые в 1591г.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета ещё далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
Глава 2. Тезаурус по теме.
2.1. Определение квадратного уравнения и его виды.
1) Алгоритм – точное предписание (правило) о выполнении в определенном порядкеуказанных операций (шагов алгоритма), позволяющее решать все задачи определенного вида.
2) Квадратным уравнением называют уравнения вида:
ax2+bx-c=0, где a, b, c – некоторые действительные числа.
а – первый или старший коэффициент;
b – второй коэффициент или коэффициент при х;
с – свободный член.
3) Квадратное уравнение называют приведенным, если старший коэффициент равен 1;квадратное уравнение называют непереведенным, если старший коэффициент отличается от 1.
4)Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трехчлен обращается в нуль.
5) Решить квадратное уравнение – значит найти все его корни или установить, что корней нет.
2.2. Решение квадратного уравнения общеизвестными способами.
Разложение левой части уравнения на множители.
Разложение на множители уравнения – это процесс нахождения таких членов или выражений, которые, будучи перемноженными, приводят к начальному уравнению.
Решим уравнение х2+10х-24=0.
Разложим левую часть уравнения на множители:
Х2+10х-24=х2+12х-2х-24=х(х+12)-2(х+12)=(х+12)(х-2).
Следовательно, уравнение можно переписать так:
(х+12)(х-2)=0.
Так как произведение равно нулю, то по крайней мере один из множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х=2,а уравнение х2+10х-24=0.
Решение квадратного уравнений по формуле
Вывод формулы:
Умножим обе части уравнения ax2+bx+c=0 , а ≠ 0, на 4а и, следовательно, имеем :
4а2х2+4аbc+4ac=0
((2ax)2+2ax ∙ b + b2)-b2+4ac=0
(2ax+b)2=b2-4ac
2ax+b= ±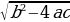
2ax =-b±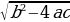
X1,2=
Выражение b2- 4 ac называют дискриминантом и обозначают D, причем
Если D0, то уравнение ax2+bx+c=0 имеет два различных корня;
Если D=0, то два одинаковых корня;
Если D
Решение уравнений с использование теоремы Виета (прямой и обратной)
1)Как известно, приведенное квадратное уравнение имеет вид:
x2+ px + q=0 (1)
Его корни удовлетворяют теореме Виета, которая при а=1 имеет вид
x 1x2= q
1x2= q
x1+x2 = -p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
А) Если свободный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.
Если p0, то оба корня отрицательные, если p
Например,
х2-3x+2=0; x1 = 2 bx2=1, так как q = 20 и q = 2 0 и p = – 3
х2 +8х + 7 = 0; х1 = – 7 и х2 = – 1, так как q = 7 0 и p = 8 0.
Б) Если свободный член q приведенного уравнения (1) отрицателен (q 0. Например, х2 + 4х – 5 = 0; х1 = – 5 и х2 = 1, так как q = – 5 0; х2 – 8х – 9 = 0; х1 = 9 и х2 = – 1, так как q = – 90.
2) Теорема Виета для квадратного уравнения ax2+bx+c=0 имеет вид :
х1х2 = 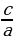 ,
,
х1+х2 = - 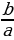 .
.
Справедлива теорема, обратная теореме Виета:
Если х1 и х2 таковы, что х1+х2 = -p, х1х2 = q, то х1 и х2 – корни квадратного уравнения
х2 + px + q = 0.
Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
Решить уравнение x2-9x+14=0
Попробуем найти два числа х1 и х2, такие, что
х1 + х2 = 9
х1х2 = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
Решить уравнение :x2+3x-28
Попробуем найти два числа х1 и х2 , такие, что
х1+х2= - 3
х1х2 = - 28
Нетрудно заметить, что такими числами будут - 7 и 4. Они и являются корнями данного уравнения.
Глава 3. Способы решения квадратных уравнений, отличные от традиционных
3.1. Метод выделения полного квадрата
• Пример
Решим уравнение х2 + 6х - 7 = 0
Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 6х в следующем виде: х2 + 6х = х2 + 2 • х • 3 .
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х и 3. Поэтому, чтобы получить полный квадрат, нужно прибавить 32, т.к.
х2+2•х•3+32=(х+3)2.
Преобразуем теперь левую часть уравнения
х2+6х-7=0,
прибавляя к ней и вычитая 32. Имеем:
х2+6х-7=х2+2• х • 3 +32 - 32-7= (х+3)2- 9 -7= (х+3)2-16.
Таким образом, данное уравнение можно записать так:
(х+ 3)2-16 = 0, т.е. (х+ 3)2 = 1б.
Следовательно, х + 3 = 4, х 1= 1, или х +3 = -4 , х2 = - 7.
3.2 Решение уравнений способом «переброски»
Рассмотрим квадратное уравнение
ах2+Ьх+ с= 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2+ аЬх + ас = 0.
Пусть ах = у, откуда х =  ; тогда приходим к уравнению
; тогда приходим к уравнению
у2+bу+ас=0,
равносильному данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получим х1 = 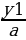 и х2 =
и х2 =  . При этом способе коэффициент а умножается на свободный член, как 6ы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как 6ы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
• Примеры
Решим уравнение
2х2 - 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2- 11у +30= 0.
С
 огласно теореме у1 = 6 х1 =
огласно теореме у1 = 6 х1 = х1 = 3
х1 = 3
У2 = 5 х2 =  х2 = 2,5
х2 = 2,5
Ответ: 2,5; 3.
3.3. Учёт свойств коэффициентов квадратного уравнения
А. Пусть дано квадратное уравнение
ах2+Ьх+ с=0,а≠0.
1. Если, а + Ь + с = 0 (т.е. сумма коэффициентов равна нулю), то
х1=1,х2= 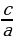 .
.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведённое квадратное уравнение: х2 +  х +
х + 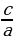 = 0.
= 0.
С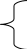 огласно теореме Виетаx1 + x2 = -
огласно теореме Виетаx1 + x2 = - 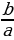
x1x2= 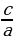
По условию, а + Ь + с = 0, откуда Ь = - a - с. Значит,
x 1+ x2 = -
1+ x2 = - 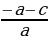 = 1 +
= 1 + 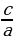
x1x2 = 1 • 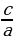
Получаем x1 = 1, x2 = 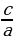 , что и требовалось доказать.
, что и требовалось доказать.
2. Если, a - b + c = 0, или b = a + c, то x1 = - 1, x2 = - 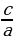 .
.
Доказательство. По теореме Виета
x 1 + x2 = -
1 + x2 = - 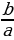
x1x2= 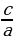
По условию, a - b + c = 0, откуда b = a + c . Таким образом,
x1 + x2 =-  = -1 -
= -1 - 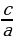
x1x2 = - 1 • (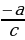 ) ,
) ,
т.е. х1 = -1 и х2 = 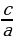 , что и требовалось доказать.
, что и требовалось доказать.
• Примеры
1.Решим уравнение 345х2 —137х — 208 = 0.
Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то х1 = 1, х2 = 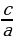 =
= 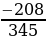 .
.
Ответ. 1;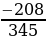 .
.
2. Решим уравнение 132x2 + 247x + 115 = 0
Решение. Т.к. a – b + c = 0 (132 - 247 + 115 = 0 ), то x1 = -1, x2 = - 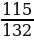
Ответ. – 1; - 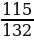 .
.
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
X1,2 =  можно записать в виде х1,2 =
можно записать в виде х1,2 = 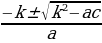
• Примеры
Решим уравнение 3x2 – 14x + 16 = 0
Решение. Имеем :a = 3, b = - 14, c = 16, k = - 7;
D=k2 – ac = (-7)2 – 3 • 16 = 49 -48 =1, D0 ,два различных корня ;
X = 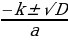 =
= 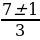 ; X1 = 2 , X2 =
; X1 = 2 , X2 = 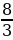 .
.
Ответ. 2; 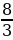 .
.
В. Приведенное уравнение х2 + px + q = 0
Совпадает с уравнением общего вида, в котором a=1, pи c = q. Поэтому для приведенного квадратного уравнения формула корней
X1,2 = 
принимает вид: x1,2 = 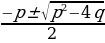 , или x1,2 = -
, или x1,2 = - 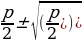 2 – q. (2).
2 – q. (2).
Формулу (2) особенно удобно использовать, когда p – чётное число.
• Пример
1. Решим уравнение х2 – 14х – 15 = 0.
Решение. Имеем: х1,2 = 7 ± 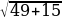 = 7 ±
= 7 ± 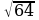 = 7 ± 8
= 7 ± 8
Ответ. X1 = 15, x2 = -1.
3.4. Решение квадратного уравнения графическим способом
Если в уравнении : х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px – q.
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости – парабола, проходящая через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи :
-прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут качаться (только одна общая точка), т.е. уравнение имеет одно решение;
-прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
• Пример
Решим графически уравнение : х2 - 3х - 4 = 0
Решение. Запишем уравнение в виде : х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13).

Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = -1 и х2 = 4.
Ответ.х1 = -1, х2 = 4.
3.5. Решение квадратных уравнений с помощью циркуля и линейки
Графический способ решения квадратных уравнений с помощью параболы не всегда удобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точность получаемых результатов невелика. Существует способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки.
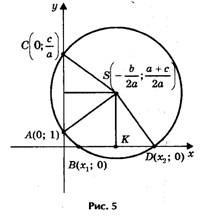
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому


Итак:
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS SK, или R a + c/2a), окружность пересекает ось Ох в двух точках В (х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
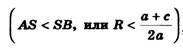
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох в точке В (х1; 0), где х1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.



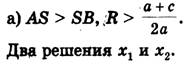


• Пример
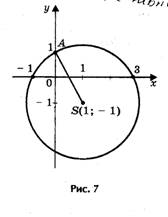
Решим уравнение х2- 2х - 3 = 0
Решение. Определим координаты точки центра окружности по формулам:
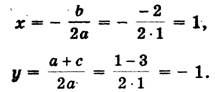
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = - 1; х2 = 3.
3.6. Решение квадратных уравнений с помощью номограмм
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициент там определить корни уравнения.
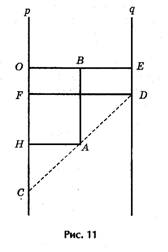
Криволинейная шкала номограммы построена по формулам
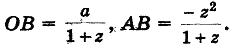
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
Если дано полное квадратное уравнение, то его надо привести к приведенному квадратному уравнению z2 + pz + q = 0
Затем второй коэффициент и свободный член из уравнения отметить на соответствующих осях p и q, полученные точки соединить прямой.
Прямая пересекает кривую шкалу в двух точках – корнях данного уравнения, если корни положительные.
Если уравнение имеет корни разного знака, то прямая пересечет кривую шкалу в одной точке – это положительный корень. Отрицательный корень находят, вычитая положительный корень из –p.
Если же корни отрицательные, то по номограмме находят два положительных корня t1 и t2 для уравнения z2 – pz + q = 0, а для уравнения z2 + pz + q = 0 корнями будут z1 = -t1, z2 = -t2
•Пример

1) Для уравнения z2 - 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0
2) Решим с помощью номограммы уравнение 2z2 - 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение:
z2 - 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения z2 - 25z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 - 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
3.7. Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми. Уравнение х2 + 10х = 39
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39».
Строим квадрат со стороной х и на его сторонах – четыре прямоугольника высотой 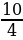 . В углах фигуры построим четыре квадрата со стороной
. В углах фигуры построим четыре квадрата со стороной 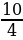 . В углах фигуры построим четыре квадрата
. В углах фигуры построим четыре квадрата 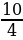 .
.









Подсчитаем площадь получившегося большого квадрата:
X2 + 4 • 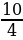 • (
• (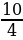 )2= x2 + 10x + (
)2= x2 + 10x + (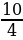 )2 • 4
)2 • 4
По условию x2 + 10x = 39, т.е. площадь большого квадрата равна
39 + ( 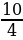 )2 • 4 = 39 + + 25 =64.
)2 • 4 = 39 + + 25 =64.
Значит, его сторона равна 8, тогда x + 2 • ( 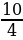 ) = 8, x = 3 (Ал–Хорезми не признавал отрицательных чисел)
) = 8, x = 3 (Ал–Хорезми не признавал отрицательных чисел)
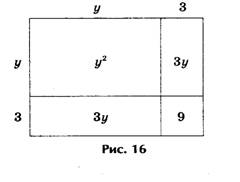
А вот, например, как древние греки решали уравнение y2 + 6y – 16 = 0
Решение представлено на рис., где у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8.
3.8. Решение уравнений с использованием теоремы Безу
Теорема Безу. Если уравнение a0xn + a1xn-1 … + an-1x + an = 0, где все коэффициенты целые, имеет целые корни, то это делители свободный член.
Следствие 2: Если b является корнем многочлена f (x), то этот многочлен делится на (x-b) без остатка.
Теорема Безу даёт возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на единицу меньше.
Таким образом, один корень найден и далее находятся уже корни многочлена, степень которого на единицу меньше степени исходного многочлена. Иногда этим приёмом – он называется понижением степени – можно найти все корни заданного многочлена.
•Пример
Решить квадратное уравнение: х2 – 4х + 3 = 0
f(x) = x2 – 4x + 3
Решение :
Делители свободного члена ±1, ±3.
Проверим 1, подставив в уравнение 1 – 4 + 3 = 0. Значит 1 – это корень данного уравнения. Тогда квадратный трёхчлен х2 - 4х + 3 делится нацело на (х-1).
Разделим f(x) на (x-1), получим:
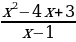 = х-3, т.е.
= х-3, т.е.
Х2 – 4х + 3 = (х-1)(х-3)
(х-1)(х-3) = 0
x – 1 = 0; х1 = 1, или х-3=0, х2=3;Ответ.х1 = 1, х2=3.
Заключение
Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание всё более полным и совершенным.
Уравнения – язык алгебры, квадратные уравнения – это фундамент, на котором построено величественное здание алгебры. Изученные способы решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных.
В ходе выполнения работы с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме. Проанализировав все новые способы решения квадратных уравнений, стало очевидным, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Некоторые ( такие как, решение с использованием теоремы Безу и решение с помощью циркуля и линейки) удобно применять, когда коэффициенты невелики, другие – допускают большие коэффициенты ( например, учёт коэффициентов): графический не всегда точен, а геометрический понятен, но громоздок. Можно сделать вывод, что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения.
Составление буклета-памятки, обобщить способы решения квадратных уравнений, которые не изучают в школе. Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ОГЭ и ЕГЭ.
Данные буклеты я раздам одноклассникам и ученикам других классов. Они могут воспользоваться собранными в буклет-памятку материалами для изучения и закрепления рациональных способов решения квадратных уравнений. В дальнейшем я планирую провести опрос, насколько интересна информация, предложенная в буклете, и используют ли они данные способы для решения квадратных уравнений, если да, то какой способ они считают наиболее простым и понятным.
Литература
1.Брадис В.М. Четырёхзначные математические таблицы для средней школы.
Изд. 57-е. – М., Просвещение, 1990. С. 83.
2.Окунев А.К. Квадратные функции, уравнения и неравенства. Пособие для учителя. – М., Просвещение, 1972.
3.Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72. С. 34.
4.Соломник В.С., Милов П.И. Сборник задач по алгебре и элементарными функциям. Пособие для учителя. Изд. 2-е. – М., Просвещение, 1970.
Интернет-ресурсы:
http://bibliofond.ru/view/aspx?id=581448
http://skolkobudet.ru/publ/4-1-0-18
http://nsportal.ru/ap/library/drugoe/2012/08/22/sem-srosobov-resheniya-kvadratnykh-uravneniy
Муниципальное бюджетное общеобразовательное учреждение г. Шахты
«Лицей № 26»
346506 г. Шахты, проспект Ленинского Комсомола, 51,тел. (8636)23-00-92
Наименование секции: математика
Исследовательская работа
Тема: «Нестандартные способы решения квадратных уравнений»
Автор работы:
Шабельник Анастасия,
8 а класс,
МБОУ г.Шахты «Лицей № 26»
Руководитель:
Авагян Элина Сергеевна
МБОУ г.Шахты «Лицей №26»
2013-2014 год
24







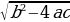

 1x2= q
1x2= q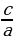 ,
,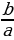 .
. ; тогда приходим к уравнению
; тогда приходим к уравнению 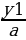 и х2 =
и х2 =  . При этом способе коэффициент а умножается на свободный член, как 6ы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как 6ы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. 
 огласно теореме у1 = 6 х1 =
огласно теореме у1 = 6 х1 = х1 = 3
х1 = 3 х2 = 2,5
х2 = 2,5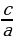 .
. х +
х + 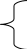 огласно теореме Виетаx1 + x2 = -
огласно теореме Виетаx1 + x2 = -  1+ x2 = -
1+ x2 = - 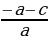 = 1 +
= 1 +  1 + x2 = -
1 + x2 = -  = -1 -
= -1 - 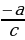 ) ,
) , 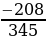 .
.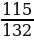
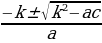
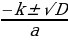 =
= 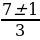 ; X1 = 2 , X2 =
; X1 = 2 , X2 = 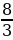 .
.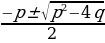 , или x1,2 = -
, или x1,2 = - 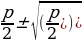 2 – q. (2).
2 – q. (2).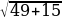 = 7 ±
= 7 ± 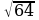 = 7 ± 8
= 7 ± 8






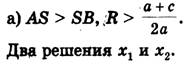



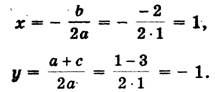



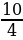 . В углах фигуры построим четыре квадрата со стороной
. В углах фигуры построим четыре квадрата со стороной 









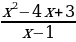 = х-3, т.е.
= х-3, т.е.









