Исследовательская работа "Тайны делимости"

Муниципальное казенное общеобразовательное учреждение

«Основная общеобразовательная школа с.Тахтоямск »

Исследовательская работа

ТАЙНЫ ДЕЛИМОСТИ ЧИСЕЛ

Работу выполнила ученица 6 класса

Шоволдаева Алтана

Руководитель:

Шоволдаева Занда Константиновна,

учитель математики 1 кв. категории

с.Тахтоямск, 2024

Содержание

Введение………………………………………………………………………3-4

Историческая справка .……………………………………………………..5-6

Раскрываем тайны делимости чисел…………………………………………..6

Свойства делимости ……………………………………………………..6

Признаки делимости на 2…………………………………..…………...7

Признаки делимости на 3…………………………………………….…8

Признаки делимости на 4……………………………………………….8

Признаки делимости на 5……………………………………………….8

Признаки делимости на 6………………………………………...……..8

Признаки делимости на 7…………………………………………….....8

Признаки делимости на 8…………………………………………….....9

Признаки делимости на 9…………………………………………….....9

Признаки делимости на 10……………………………………………...9

Признаки делимости на 11……………………………………………...9

Признаки делимости на 12……………………………………………...10

Признаки делимости на 13……………………………………...………10

Признаки делимости на 14……………………………………………..11

Признаки делимости на 15…………………………………………......11

Признаки делимости на 19………………………………………...........11

Признаки делимости на 25………………………………………...……11

Признаки делимости на 50…………………………………………….12

Выводы………………………………………………………………………….12

Заключение……………………………………………………………………..12 Список используемой литературы …………………………………………...13

Приложения…………………………………………………………………14-15

Введение.

Изучая на уроках математики тему «Делимость чисел», в 5 классе мы познакомились с признаками делимости на 2, 3, 5, 9 и 10, узнали, какие числа являются простыми и составными. В шестом классе мы продолжили эту тему. И у меня возникли вопросы: «А существуют ли признаки делимости на другие числа?». Так появилась идея начать работу над учебным проектом «Признаки делимости» и я решила назвать свою работу «Тайны делимости чисел». Было предположено, что если можно определить делимость чисел на 2, 3, 5, 9 и 10, то должны быть признаки, по которым можно определить делимость и на другие числа.

В этом году на уроке математики я познакомилась с такими понятиями как наибольший общий делитель и наименьшее общее кратное чисел. Так вот чтоб найти НОД и НОК, нужно числа разложить на простые множители. И тут я поняла, что знание признаков деления очень облегчает работу.

Формулировка темы: Тайна делимости чисел.

Актуальность исследования:

Проблема исследования:

Объект: числа. Предмет: математика.

Цель: раскрыть тайны делимости и найти признаки делимости, которых нет в школьной программе.

Задачи:

1) Самостоятельно исследовать делимость чисел.

2) Изучить дополнительную литературу с целью ознакомления с другими признаками делимости.

3) Объединить и обобщить признаки из разных источников.

4) Сделать вывод.

Гипотеза: Мы предполагаем, что если можно определить делимость чисел на 2, 3, 5, 9 и 10, то должны быть признаки, по которым можно определить делимость и на другие числа.

В результате изучения различной литературы, наша гипотеза была подтверждена.

Методы исследования:

1. Изучение литературы и электронных источников.

2. Систематизация и обобщение полученной информации.

3. Применение изученной теории при решении проблемных задач.

Этапы исследования:

1. Постановка цели.

2. Поиск информации.

3. Обработка информации.

4. Применение найденных признаков деления на практике.

Практическая значимость: данное исследование будет полезным для учащихся при самостоятельной подготовке к выпускным и вступительным экзаменам. А также будет полезно и для учеников, целью которых стали высокие места на всероссийских олимпиадах по математике.

Историческая справка

Блез Паскаль – один из самых знаменитых людей в истории человечества. Паскаль родился 19 июня 1623 в Клермон-Ферран, в семье высокообразованного юриста. Отец Паскаля имел хорошее образование и решил самостоятельно заниматься образованием мальчика. Блез рос одарённым ребёнком и рано проявил выдающиеся математические способности. Его отец старался обучить мальчика древним языкам, настаивая, чтобы тот не отвлекался на разного рода пустяки. Как-то раз, на очередной вопрос сына о том, что такое геометрия, отец кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции. Однако тут же запретил ему всякие исследования в этой области. Но запретный плод сладок, и Блез, закрывшись в своей спальне, принялся углем выводить на полу различные фигуры и изучать их. Когда отец случайно застал его за одним из таких самостоятельных уроков, он был потрясен: не знавший даже названий фигур, мальчик доказывал их свойства. Так постепенно раскрывался гений Блеза Паскаля.

Отец Блеза был сборщиком налогов, и, наблюдая за его бесконечными утомительными расчетами, Паскаль, в возрасте 19 лет, задумал создать вычислительное устройство, которое могло бы помочь этой работе. Он работал над этим устройством в течение трех лет. Устройство, называющееся "Паскалиной", выглядело как ящик, наполненный многочисленными связанными друг с другом шестерёнками. Складываемые числа вводились соответствующим поворотом колес. За несколько лет Паскаль построил около 50 вариантов своей машины. Паскаль получил лично от короля Патент на изобретение с сохранением авторских прав на ее изготовление и продажу. Изобретённый Паскалем принцип связанных колёс почти на три столетия стал основой создания большинства вычислительных устройств. Во Франции она оставалась в употреблении до 1799г., а в Англии даже до 1971 года.

Но это было далеко не все, на что оказался способен одаренный юноша. К 30-ти годам закончил ряд работ по арифметике, алгебре, теории вероятностей и теории чисел. Паскаль нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, который опубликовал в трактате "О характере делимости чисел".

Раскрываем тайны делимости чисел

Среди всех арифметических действий самым «строптивым» является деление. Оно имеет особенности, отличные от тех, которые имеют другие арифметические действия. Например, для остальных арифметических действий нуль — равноправное число. Его можно и прибавлять, и вычитать, оно может быть множителем. А вот делителем — никогда! Делить на нуль нельзя!

«Характер» деление проявляет не только в том, что касается нуля. В математике уделяется много внимания целым числам и действиям над ними. Так вот и здесь «капризничает» лишь одно действие — деление. Деление без остатка не всегда можно выполнить на множестве целых чисел.

Все эти особенности деления способствовали появлению таких понятий, как простые числа, наибольший общий делитель(НОД), наименьшее общее кратное(НОК) ...

Делители и кратные.

Говорят, что натуральное число m делится без остатка на натуральное число n, если есть такое натуральное число a, что m=n*a. Натуральное число n называют делителем натурального числа m, а число m – кратным числа n.

Простые и составные числа.

Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.

Натуральное число, у которого более двух делителей, называют составным.

Число 1 не относится ни к простым, ни к составным числам.

Свойства делимости.

1. Если один из множителей делится на некоторое число, то и произведение делится на это число.

Пример. Проверим, делится ли 2400 на 25, не выполняя деления.

2400=24*100=24*25*4=25*96

2400/25=96

2. Если каждое из двух чисел делится на на некоторое число, то и их сумма или разность делятся на это число.

Пример. Проверим, делится ли сумма чисел 22,55 и 77 на 11, не выполняя деления:

22+55+77=2*11+5*11+7*11=11(2+5+7)=11*14.

Значит сумма делится на 11.

3. Пусть число a делится на c, а число c делится на число d. Тогда число a также делится на число d.

4. Если число a делится на число c, то для любого натурального n число aⁿ делится на cⁿ.

Признак делимости.

Признак делимости - это правило, по которому, не выполняя деления, можно установить, делится ли одно число на другое.

Признак делимости на 2.

Итак, самый простой и часто применяемый из них. Проверка, делится ли число на 2, не требует никаких вычислений: либо оно четное и делится на 2, либо нечетное и не делится на 2.

Признак делимости на 3.

Если же решение задач по алгебре требует установить делимость числа на 3, то придется выполнить простейшие вычисления, а именно сложить все цифры числа и, если полученный результат делится на 3, то и само число делится на 3. Например, число 528 на 3 делится, так как 5 + 2 + 8 = 15, а 15 на 3 делится без остатка.

Признак делимости на 4.

Следующий признак – деление на 4. Здесь стоит обратить внимание на последние две цифры – если образуемое ими число делится на 4, то и все число делится на 4. Кроме того, все числа, оканчивающиеся двумя нулями, так же делятся на 4.

Признак делимости на 5.

Правило делимости на 5 так же просто, как и делимость на 2, необходимо посмотреть на последнюю цифру этого числа. Если она равна 5 или 0, то будьте уверены - это число разделится на 5 без всяких проблем.

Признак делимости на 6.

Уже более интересно определять делимость на 6. В этом случае сначала стоит установить четность числа, так как нечетные числа на 6 вообще не делятся, а затем проверить его на делимость на 3, что, впрочем, тоже достаточно просто.

Кстати, упомянутое уже число 528, делится на 3 и, поскольку оно четное делится на 6.

Признаки делимости на 7.

А вот с делимостью на 7 вы вряд ли познакомитесь в школе. Дело в том, что это достаточно сложный признак. Если утроенное число десятков, сложенное с числом единиц делятся на 7, то само число делится на 7.

Например: рассмотрим число 154 (15*3+4=49, 49 делится на 7, значит и 154 делится на 7).

Признак делимости на 8.

Признак делимости на 8 очень похож на признак делимости на 4, но здесь нужно обратить внимание уже на 3 последние цифры. Если они нули или делятся на 8, то и все число тоже будет делиться на 8.

Признак делимости на 9.

Признаком делимости на 9 пользуются достаточно часто, и знать его нужно обязательно. Так же как и при проверке делимости на 3, необходимо сложить все цифры, и если полученное число делится на 9, то и исходное число тоже делится на 9.

Признак делимости на 10.

И, конечно же, всем известен признак делимости на 10. Просто в конце должен стоять ноль!

Признаки делимости на 11.

Число делится на 11, если разность суммы цифр, стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.

Разность может быть отрицательным числом или быть равной нулю, но обязательно должна быть кратной 11.

Испытаем число 100397.

Нумерация идет слева направо.

1+0+9=10

0+3+7=10

10-10=0, 0 кратно 11, значит, 100397 делится на 11.

Можно проверить делимость числа на 11 другим способом:

Испытуемое число разбивают справа налево на группы по две цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.

Например, испытаем число 15235.

Разбиваем на группы

1. 52. 35 и складываем их:

1+52+35=88.

88 делится на 11, значит, 15235 делится на 11.

Признак делимости на 12.

Проверьте делимость интересующего нас числа на 3 и 4. Число делится на 12 в том, и только в том случае если оно одновременно делится на 3 и 4. Например: 12653400 - делится на 3 и 4, а значит и на 12.

Признак делимости на 13.

Число делится на 13 тогда и только тогда, когда результат вычитания последней цифры умноженной на 9 из этого числа без последней цифры делится на 13.

Например:

858 делится на 13, так как 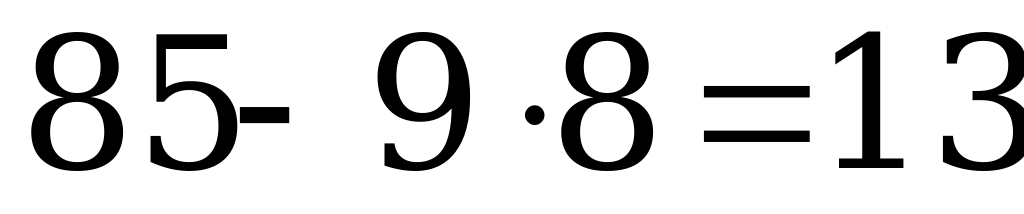делится на 13.

Признак делимости на 14.

Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.

Пример:

Число 45612 делится на 2 и на 7, значит, оно делится и на 14.

Признак делимости на 15.

Для того чтобы число делилось на 15, необходимо и достаточно, чтобы оно делилось на 5 и на 3, т.е. чтобы оно оканчивалось нулем или пятеркой и, кроме того, сумма его цифр делилась на 3.

Например: 1146795

1+1+4+6+7+9+5=33, значит, число кратно 3.

Признак делимости на 19.

Число делится на 19 без остатка тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19. Например; требуется определить, делится ли на 19 число 1026.

Применим последовательно признак делимости. Число десятков в признаке надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.

1) 1 0 2 +2 ∙ 6= 114

2) 11+ 2∙4=19

В результате выполнения последовательных двух шагов мы получили число 19, которое делится на 19, следовательно, число 1026 делится на 19.

Признак делимости на 25.

Число делится на 25 тогда и только тогда, когда две его последние цифры либо нули, либо образуют число, делящееся на 25. Пример: Число 34650 делится на 25, т.к. 50 делится на 25.

Признак делимости на 50.

Чтобы число делилось на 50, надо, чтобы на конце записи числа две последние цифры делились бы на 25 и представляли бы четное число. А этому условию удовлетворяют только числа 50 и 100, но 100- трехзначное число, значит, запись числа должна оканчиваться на 00 или 50.

Например:

6957200, 67906850.

Выводы.

В ходе работы над исследовательской работой:

1. Нашли и познакомились с различными источниками информации по теме делимость чисел.

2. Систематизировали полученную информацию.

3. Научились пользоваться признаками для определения делимости чисел.

Все это позволило более широко изучить тему делимости чисел, расширило наш математический кругозор.

Считаем, что применение признаков делимости чисел в изучении математики является эффективным. Знание их значительно ускоряет решение многих задач. Предложенный материал «Признаки делимости чисел» можно использовать как на уроках математики, так и во внеклассных занятиях.

Заключение.

Работая над поставленной проблемой, мы выяснили, что кроме известных нам признаков делимости на 2, 3, 5, 9 и 10 существуют еще признаки делимости на 4, 6, 7, 8, 11, 12, 13, 14, 15, 19 , 25 и 50.

В дальнейшем планируем продолжить изучение признаков делимости чисел. В частности планируем рассмотреть универсальный признак делимости, с помощью которого можно получить признак делимости на любое натуральное число.

Список используемой литературы.

• Математика: 5 класс: базовый уровень: учебник: в 2 частях/ Н.Я. Виленкин, В.И. Жохов, А.С. Чеснаков [и др.]. - 3-е изд., перераб. - Москва: Просвещение, 2023.

• Математика: 6 класс: базовый уровень: учебник: в 2 частях/ Н.Я. Виленкин, В.И. Жохов, А.С. Чеснаков [и др.]. - 4-е изд., стер. - Москва: Просвещение, 2024.

• Всероссийский научно-методический журнал Математика. Всё для учителя, 2017г.

• Г. И. Глейзер «История математики в школе 7 – 8 классы», Москва, 1982, «Просвещение».

• «1001 вопрос и ответ. Большая книга знаний» Москва 2004 «Мир книги»

• Я.И. Перельман. Занимательная Алгебра, - М.: Триада-Литера, 1994.-199с.

Электронные источники.

• Журнал "Hard" n "Soft" (online) №6-2003.

• Энциклопедический ресурс www.rubricon.com (Большая советская энциклопедия, Иллюстрированный энциклопедический словарь).

Приложения

А теперь попробуем выяснить:

1. делится ли число 6321 на 7;

делится ли число 3333 на 11;

делится ли число 154 на 11;

делится ли число 2⁹*3 на 6?

Если утроенное число десятков, сложенное с числом единиц делятся на 7, то само число делится на 7.

632*3+1=1897

1897/7=271 значит 6321 делится на 7.

Испытуемое число разбивают справа налево на группы по две цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.

33.33

33+33=66

66/11=6, т.е. число 3333 делится на 11.

1.54

1+54=55

55 делится на 11, а значит число 154 делится на 11.

2⁹*3=2⁸*2*3=2⁸*6, т.е. делится на 6.

2. Выяснить делится ли на 3 число a, если число 5a делится 3; делится ли на 6 число a, если число 15a делится на 6?

5a делится на 3. Если один из множителей делится на три, то и все произведение делится на три.

15a делится на 6, 15 не делится на 6, значит a делится на 6.

3. Доказать, что произведение трех последовательных натуральных чисел делится на 6.

7*8*9=504

504 четное, значит делится на 2.

Проверим делимость на три: 5+0+4=9, 9 делится на три, значит число 504 делится на три, а значит делится и на 6.

17