Исследовательская работа на тему «Практическое применение процентов в повседневной жизни»

Муниципальное общеобразовательное бюджетное учреждение

средняя общеобразовательная школа с. Леуза

Исследовательская работа

по теме «Практическое применение процентов в повседневной жизни»

Выполнила:

ученица 9 класса

Власова Елена

Учитель математики:

Клыкова Т.А.

2016 год

В любом открытии есть 99 % труда и потения

И только 1% таланта и способностей.

                                 Л. Магницкий

Проценты – один из наиболее сложных и важных разделов математики. У многих учеников эта тема вызывает затруднения при решении задач. Понимание и умение решать задачи на проценты крайне важно, т.к. практическое применение этих задач очень обширно. Применение процентов можно встретить в любых магазинах, банках, госучреждениях (администрациях, больницах, школах), на заводах и других предприятиях. Мне стало интересно разобраться с темой «Практическое применение процентов в повседневной жизни», поэтому я решила провести небольшое исследование.

Целью моей исследовательской работы является – расширение и практическое применение знаний о вычислении процентов полученных на уроках алгебры.

Гипотеза : Важна ли тема «Проценты» в жизни взрослых?

Для достижения цели, были поставлены следующие задачи задачи:

• При помощи специальной литературы и интернет изучить историю возникновения процентов.

• Рассмотреть основные задачи на применение процентов

• Показать применение процентов при решении реальных задач в различных сферах жизнедеятельности человека.

• Провести статистическое исследование

• Обобщить результаты. Сделать выводы

Объектом исследования является комплекс задач на проценты

Предмет исследования – повседневное практическое использование математических вычислений поставленных задач  с процентами.

Актуальность и практическая значимость: необходимо повышать уровень знаний учащихся во время изучения процентов в школе, так как сейчас в вариантах ОГЭ и ЕГЭ встречаются задачи на проценты, и эти задачи очень часто вызывают затруднения. Во взрослой жизни во многих жизненных ситуациях люди обращаются к этой теме.

Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления. Без понятия «процент» нельзя обойтись ни в бухгалтерском учёте, ни в финансовом анализе, ни в статистике. Проценты – математическое понятие, которое часто встречается в повседневной жизни. Любой человек должен уметь решать задачи, предлагаемые самой жизнью. Мы платим налоги. Как посчитать материальное вознаграждение, которое получаем мы, когда кладем деньги на депозит, какое вознаграждение получает банк, когда мы берем кредит, ипотеку. Все эти вопросы решает знание процентов. Везде – в газетах, по радио, телевидению и на работе обсуждаются повышение цен, зарплат, пенсии, рост стоимости акций, снижение покупательской способности населения. Решение математических задач практического содержания позволяет убедиться в значении математики для различных сфер человеческой деятельности, увидеть широту возможных приложений математики, понять её роль в современной жизни.

История возникновения процентов.

Слово «процент» происходит от латинского слова “pro centum”, что означает «со ста». Идея выражения частей целого постоянно в одних и тех же долях родилась ещё в древности у вавилонян, в их клинописных табличках уже содержались задачи на расчёт процентов. Были известны проценты и в Индии, где с давних пор вёлся счёт в десятичной системе счисления. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов. В русском языке слово «процент» имеет и другое смысловое значение − выражает тот факт, что заёмщик помимо возврата предоставленных ему кредитором денежных средств должен дополнительно заплатить кредитору за использование этих средств. Об этом говорит, например, объявление: «Банк предоставляет населению кредиты под проценты».

Денежные расчеты с процентами были особенно распростране­ны в Древнем Риме. Римляне называли процентами деньги, кото­рые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый про­цент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян процен­ты перешли к другим народам.

В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять процен­ты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таб­лицы, которые составляли коммерческий секрет фирмы.

В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584г. он впервые опубликовал таблицу процентов. Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т.д. Знак «%» происходит, как полагают, от итальянского слова cento(сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения буквы t в наклонную черту произошёл современный символ для обозначения процента. Другая версия происхождения этого знака заключается в том, что в Париже в 1685 году наборщик книги-руководства по коммерческой арифметике допустил опечатку – вместо cto написал %. Долгое время под процентами понимались исключительно при­быль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Уже в далекой древности широко было распространено ростовщичество - выдача денег под проценты. Разность между той суммой, которую возвращали ростовщику, и той, которую первоначально взяли у него, называлась лихвой. Так, в Древнем Вавилоне она составляла 20 % и более! Известно, что в XIV-XV вв. В Западной Европе широко распространились банки - учреждения, которые давали деньги в долг князьям, купцам, ремесленниками и т. д. Конечно, банки давали деньги не бескорыстно: за пользование предоставленными деньгами они брали плату, как и ростовщики древности. Эта плата выражалась обычно в виде процентов к величине выданных в долг денег. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. [9] Ныне процент - это частный вид десятичных дробей, сотая доля целого (принимаемого за еди­ницу). Процентами очень удобно пользоваться на практике, так как они выражают части целых в одних и тех же долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целым. Процент – сотая доля числа, принимаемого за целое. [1] Если речь идет о проценте от данного числа, то это число и принимается за 100 %. Например, 1 % от зарплаты - это сотая часть зарплаты; 100 % зарплаты - это сто сотых частей зарплаты, т. е. вся зарплата. Сотая часть метра – это сантиметр, сотая часть центнера - это килограмм. 1% - одна сотая доля числа. Как известно из практики, с помощью процентов часто показы­вают изменение той или иной конкретной величины. Такая форма является наглядной числовой характеристикой изменения, характе­ризующей значимость произошедшего изменения. Величина, выраженная в процентах, является более наглядной, понятной, ее легко сравнить с другими значениями.

Виды задач на проценты и способы их решения.

1. Нахождение процентного отношения двух чисел.

Из 25500 было удержано в качестве подоходного налога 3315 рублей. Какой процент от заработной суммы составляет подоходный налог?

Решение.

1. способ. 25500:100=255(р) – составляет 1%

3315:255=13% – составляет подоходный налог.

2. способ.

3. способ. 25500 – 100%

3315 – х %

Составим пропорцию

=13%

Магазин делает пенсионерам скидку на определенное количество процентов от стоимости покупки. Сколько процентов составляет скидка, если буханка хлеба стоила в магазине 24 рубля, а пенсионер заплатил 21 рубль 12 копеек?

Решение: 1 рубль = 100 копеек. Значит, 21 рубль 12 копеек — это 21,12 рубля. Пенсионер заплатил за хлеб на 24−21,12=2,88 рубля меньше полной цены. Значит, скидка составила

2,8824⋅100%=12%

Ответ: 12%

2) Задача о нахождении процента от числа.

Задача.  Стоимость проезда в электричке составляет 80 рублей. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить проезд для группы из трех взрослых и пяти школьников?

Решение: Билет для школьника стоит 100%−50%=50% от полной цены билета. Значит, такой билет стоит

50:100⋅80=40 рублей.

Теперь найдем стоимость проезда для указанной группы:

3⋅80+5⋅40=240+200=440

Ответ: 440

3) Задача о нахождении числа по его процентам.

 Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480 кг волокна?

Решение: Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби).
480 : 0,24= 2000 кг = 2 т

Ответ: 2 т.

4)  Увеличение на р% 

 Банк платит доход в размере 4% в месяц от величины вклада. На счет положили 300 тысяч рублей, доход начисляют каждый месяц. Вычислите величину вклада через 3 месяца.

Решение: 100 + 4 = 104 (%) = 1,04 – доля увеличения вклада по сравнению с предыдущим месяцем.

1. 300 • 1,04 = 312 (тыс. р) – величина вклада через 1 месяц.

2. 312 • 1,04 = 324,48 (тыс. р) – величина вклада через 2 месяца.

3. 324,48 • 1,04 = 337,4592 (тыс. р) = 337 459,2 (р)-величина вклада через 3 месяца.

Или можно пункты 2-4 заменить одним: 300•1,043 =337,4592(тыс. р) = 337 459,2 (р) – величина вклада через 3 месяца.

Ответ: 337 459,2 рубля

5) Уменьшение на р%

Пример. (Вариант 1 № 16. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 -80с)

Спортивный магазин проводит акцию. Любой джемпер стоит 400 рублей. При покупке двух джемперов – скидка на второй джемпер 75%. Сколько рублей придется заплатить за покупку двух джемперов в период акции?

Решение: Согласно условию задачи получается, что первый джемпер покупается за 100 % его исходной стоимости, а второй за 100 – 75 = 25 (%), т.е. всего покупатель должен заплатить 100 + 25 = 125 (%) от исходной стоимости. Далее можно рассмотреть решение тремя способами.

1 способ. 400 рублей принимаем за 100 %. Тогда в 1% содержится 400 : 100 = 4 (руб.), а в 125 %
4 • 125 = 500 (руб.)

2 способ. Процент от числа находится умножением числа на дробь, соответствующую проценту или умножением числа на данный процент и делением на 100. 400 • 1,25 = 500 или 400 • 125/100 = 500(руб.)

3 способ. Применение свойства пропорции:
400 руб. – 100 %
х руб. – 125 %, получим х = 125 • 400 / 100 = 500 (руб.)

Ответ: 500 рублей.

Решение задач на смеси и сплавы, с использованием понятий «процентное содержание», «концентрация», «% -й раствор».

Самые простые задачи этого типа приведены ниже.

Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.

Решение:

10 • 0,15 = 1,5 (кг) соли.

Ответ: 1,5 кг.

Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором (например, 15%-й раствор соли).

Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?

Решение: Процентное содержание вещества в сплаве - это часть, которую составляет вес данного вещества от веса всего сплава.

1. 10 + 15 = 25 (кг) - сплав;

2. 10 : 25 • 100% = 40% - процентное содержание олова в сплаве;

3. 15 : 25 • 100% = 60% - процентное содержание цинка в сплаве.

Ответ: 40%, 60%.

В задачах этого типа основным является понятие «концентрация». Что же это такое? Рассмотрим, например, раствор кислоты в воде.

Пусть в сосуде содержится 10 литров раствора, который состоит из 3 литров кислоты и 7 литров воды. Тогда относительное (по отношению ко всему объему) содержание кислоты в растворе равно 0,3. Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково:0,3∙100=30% . Как видно, переход от концентрации к процентному содержанию и наоборот весьма прост.

Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:

• концентрацией данного вещества в смеси (сплаве) называется величина с=m:М

• процентным содержанием данного вещества называется величина с×100%;

Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.

Если концентрация вещества в соединении по массе составляет P%, то это означает, что масса этого вещества составляет P% от массы всего соединения.

Пример. Концентрация серебра в сплаве 300 г составляет 87% .

Решение: 300 • 0,87 = 261 (г).

Это означает, что чистого серебра в сплаве 261 г.

В этом примере концентрация вещества выражена в процентах.

Отношения объема чистого компонента в растворе ко всему объему смеси называется объемной концентрацией этого компонента.

Сумма концентраций всех компонентов, составляющих смесь, равна 1.

Если известно процентное содержание вещества, то его концентрация находится по формуле:
К = P/100%,
где К - концентрация вещества;
P - процентное содержание вещества (в процентах).

Решение более сложных задач на проценты.

Пример. (Вариант 8 № 22. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 - 80с)

Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?

Решение: Если в свежих фруктах содержится 75% воды, то сухого вещества будет 100 – 75 = 25 (%), а высушенные – 25%, то сухого вещества в них будет 100 – 25 = 75 (%).

При оформлении решения задачи, можно использовать таблицу:

Общая масса, кг   |   Концентрация сухого вещества   |   Масса сухого вещества

Свежие фрукты х 25% = 0,25 0,25 • х

Высушенные фрукты 45 75% = 0,75 0,75 • 45 = 33,75

Т.к. масса сухого вещества для свежих и высушенных фруктов не меняется, то получим уравнение:

0,25 • х = 33,75;
х = 33,75 : 0,25;
х = 135 (кг) – требуется свежих фруктов.

Ответ: 135 кг.

 Решение задач на проценты, с использованием понятия коэффициента увеличения (уменьшения).

Чтобы увеличить положительное число А на р процентов, следует умножить число А на коэффициент увеличения К = (1 + 0,01р).

Чтобы уменьшить положительное число А на р процентов, следует умножить число А на коэффициент уменьшения К = (1 – 0,01р).

Пример. (Вариант 29 № 22. ОГЭ-2015. Математика. Тип. экзаменационные варианты: 36 вариантов/ под ред. Ященко, 2015 - 224с)

Цена товара была дважды снижена на одно и то же число процентов. На сколько процентов снижалась цена товара каждый раз, если его первоначальная стоимость 5000 рублей, а окончательная 4050 рублей?

Решение: 1 способ. Т.к. цена товара снижалась на одно и то же число %, обозначим число % за х. Пусть в первый и второй раз цена товара была понижена на х%, тогда после первого понижения цена товара стала (100 – х) %.

Составим пропорцию
5000 руб. – 100%
у руб. – (100 – х)%, получим у = 5000 • (100 – х) / 100 = 50 • (100 – х) рублей – стоимость товара после первого понижения.

Составим новую пропорцию уже по новой цене:
50 • (100 – х) руб. – 100%
z руб. – (100 – х)%, получим z = 50 •(100 – х) (100 – х) /100 = 0,5•(100 –х) 2 рублей – стоимость товара после второго понижения.

Получим уравнение 0,5 • (100 – х)2 = 4050.

Решив его, получим, что х = 10 % .

2 способ. Т.к. цена товара снижалась на одно и то же число %, обозначим число % за х, х % = 0,01 х.

Используя понятие коэффициента уменьшения, сразу получаем уравнение: 5000 • (1 – 0,01х)2 = 4050.

Решив его, получим, что х = 10 %.

Ответ: на 10 % снижалась цена товара каждый раз.

Старинный способ решения задач на смеси, сплавы и растворы (правило креста).

Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.

Данный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.

Задача: Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.

Решение: Применим правило “креста”. Составим схему:

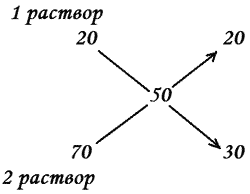
Значит, 100 г смеси составляют 20 + 30 = 50 частей.

100 : ( 20 + 30 ) = 2 г - на 1 часть.

2 * 20 = 40 г – 20% раствора

2 * 30 = 60 г – 70 % раствора

Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора.

Использование процентов людьми разных профессий.

В наше время почти во всех областях человеческой деятельности встречаются проценты. Мы решили выяснить, какие задачи на проценты в нашем селе решают люди разных профессий. Наиболее часто проценты используются в торговле: скидки, наценки, прибыль, сезонные изменения цен на товары, налог на прибыль. Продавец производит расчёт стоимости товара во время периода скидок, расчёт реального дохода от торговли, изменение товарооборота по сравнению с предыдущим периодом.  В нашем магазине «Добрый» мы сравнили цены на некоторые продукты в сентябре и в октябре. Результаты мы оформили в виде диаграммы и сделали вывод о том, что в октябре цены на подсолнечное масло, рис и чай повысились на 15%, а на бананы и печенье – на 21%.

В энерго-сбытовой компании, рассматривают реализация электроэнергии

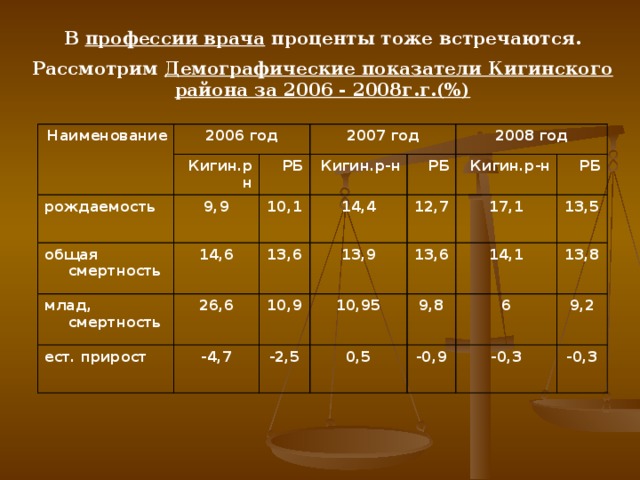
В профессии врача проценты тоже встречаются рассмотрим Демографические показатели Кигинского района за 2006 - 2008г.г.(%)

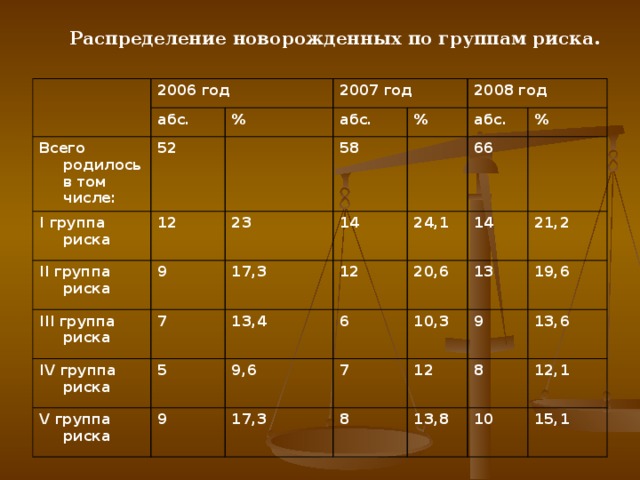
Распределение новорожденных по группам риска

В нашей школе используют процентные вычисления в своей работе учителя

Помимо перечисленных немногих сфер жизнедеятельности, где можно встретить проценты, самой распространенной является, конечно, же банки.

Сегодня банки предлагают деньги в кредит на каждом шагу и практически любую вещь в магазине можно приобрести в рассрочку. Тех, кто берет в долг деньги в банке, называют заемщиками, а величину взятых у банка денег, называют кредитом. Кредит – ссуда, предоставление ценностей (денег, товаров) в долг. Популярность кредитования в нашей стране растет из года в год. Как показывает статистика, с 2001 года по 2016 год объем выдаваемых банками кредитов выросла в 95 раз. Огромный интерес физических лиц к разному роду кредитам вполне понятен, люди хотят упростить свою жизнь и жить лучше. С приобретением квартиры, автомобиля, загородного дома или другой дорогостоящей покупки в кредит покупатель избавляется от необходимости копить деньги и получает возможность наслаждаться жизнью. Однако при всей выгодности приобретения любой покупки в кредит перед каждым человеком встает проблема ежемесячной выплаты ощутимой суммы из зарплаты и ожидание того момента, когда наконец-то он освободится от финансовой кабалы. Сегодня банки и магазины очень умело пользуются создавшимся положением, деньги в кредит предлагаются на каждом шагу и практически любую вещь можно в магазине приобрести в рассрочку. У каждого человека свое отношение к кредитам. Если некоторые люди считают, что с кредитными деньгами жить лучше, то некоторые принципиально не берут деньги в долг и не покупают ничего в рассрочку, предполагая, что доступные кредиты загоняют людей в долговую яму.

Вот какие преимущества дает кредитование:

• наконец-то вы можете приобрести то, о чем давно мечтали;

• в условиях инфляции кредитные ставки могут со временем оказаться заметно ниже роста цен, в этом случае можно даже сэкономить деньги;

• осуществив заветную покупку сегодня, через год можно радоваться, увидев заметный рост цен из-за инфляции;

• вы наберетесь опыта кредитования, что будет полезно вам в будущем;

• если в первый раз вы своевременно погасите проценты, то будете иметь положительную кредитную историю, что облегчить получение кредита в будущем.

Однако любой кредит дается только на некоторое время, за которое вам надо выплатить его с процентами. Поэтому, прежде чем брать его, надо знать следующее:

• если вы берете кредит на длительный срок, есть риск за это время потерять работу или заболеть, что сделает невозможным выплату долга;

• проценты за кредит на длительный срок делают покупку дороже в два, а то и в три раза;

• если вы берете кредит на большую сумму, то для оформления его требуется много времени и нервов, чтобы оформить документы;

• чтобы получить кредит, банк попросит от вас подтверждения о ваших доходах, а в некоторых банках большие суммы дают только под залог имущества;

• многие кредиты выплатить досрочно невыгодно, так как банк подвергает в этом случае вас к дополнительным штрафным санкциям из-за уменьшения своих доходов.

Конечно, существование у современного человека такого инструмента как кредит, это безусловный плюс. Ведь оно дает возможность человеку приобрести то, что жизненно необходимо в том случае, когда денег нет, а срочно нужны деньги на операцию, на учебу ребенка или на покупку холодильника, когда тот неожиданно сломался. Но брать кредит в тех случаях, когда вам просто хочется иметь шикарный автомобиль или квартиру большей площади, не обдумав все возможные минусы кредитования, не стоит. При существующих процентах на автокредитование примерная сумма ежемесячных платежей составляет от 2% до 3% от первоначальной стоимости автомобиля. С учетом ежегодных трат на страхование автомобиля, новый автомобиль будет обходиться примерно на 30-35% дороже реальной стоимости. Поэтому покупать автомобиль в кредит выгодно в том случае, если у вас есть точная информация, что через некоторое время цены на эти модели автомобиля вырастут на 35%. В этом случае покупая автомобиль в кредит можно даже сэкономить. Также выгодным может оказаться ипотечный кредит, так как цены на квартиру за последние годы стремительно растут вверх. Как показывает опыт мировой практики, за последние 100 лет цены на недвижимость стабильно дорожают. Поэтому копить на квартиру годами и снимать жилье не выгодно. Если позволяют доходы семьи, надо оформлять ипотечный кредит. Но нужно помнить, что купленная на ипотеку квартира - это заложенное имущество, которую могут отобрать, если вы не сможете вернуть требуемую сумму. Брать потребительский кредит оправданным может быть только в том случае, если вам деньги необходимы на неотложные нужды. Например, на оплаты учебы или лечения. Кредиты на бездумные траты для покупки очередной норковой шубы или сотового телефона не оправдывают себя. Прежде чем их брать, остановитесь и спросите себя, улучшит ли вашу жизнь безумная гонка за "новым и лучшим"?

Я живу в России и считаю, что в данный момент для нас очень важно научиться грамотно пользоваться полезной услугой под названием «кредит» — уметь сравнивать доступные варианты и выбирать оптимальное предложение, разбираться в ценообразовании и не переплачивать лишнего.

Проценты в повседневной жизни.

Трудно найти область нашей жизни, где бы не применялись проценты. Как известно, выводы опираются на анализ. А самый удобный и быстрый способ анализировать – процентный. Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это даёт возможность упрощать расчёты и легко сравнивать части между собой и с целыми. В повседневной жизни мы постоянно сталкиваемся с процентами. Например: Динамика численности населения: Численность населения Кигинского района по состоянию на 1 января 2017 года составила 17582 человека, численность населения по состоянию на 1 января 2016 года составила 18007 человека. За год численность населения уменьшилась на 2,36%. Согласно Всероссийской переписи населения 2010 года: татары — 51,4%, башкиры — 41,5%,русские — 5,6%, лица других национальностей — 1,5%

Коммунальные услуги. Цены за пользование газом и электроэнергией постоянно повышаются. Мы сравнили тарифы на электроэнергию и газ в январе и декабре текущего года. Данные приведены в таблице.

Проценты в быту: Для засолки огурцов был нужен 9% раствор уксусной кислоты, в наличии был 70% раствор. Мама попросила меня посчитать сколько надо добавить воды в 20 грамм 70% раствора, чтобы получить 9% раствор. Решение: Это легко считается по так называемому "правилу креста":

70     9      70% эссенция
   \   /
     9          нужная смесь
   /   \
 0     61     вода
т. е. эссенцию и воду надо смешивать в соотношении 9:61,
поэтому к 20 г эссенции нужно добавить 20·61/9 = 135,5 г воды.
 Использование процентов в периодической печати. В прессе достаточно часто используется понятие процента. Если внимательно читать газеты, то за цифрами процентов можно увидеть реальное положение вещей. Проценты нужно знать каждому человеку, иначе нельзя понять пользу информации. Из СМИ мы слышим в декабре 2016 года уровень инфляции в России составил 0,40%, что на 0,04 меньше, чем в ноябре 2016 года и на 0,37 меньше, чем в декабре 2015 года. Вместе с этим, инфляция с начала 2016 года составила 5,38%, а в годовом исчислении - 5,38%. Это значит, что в 2017 году нам стоит ожидать повышение уровня цен на товары и услуги. То есть, на одну и туже сумму денег по происшествии некоторого времени можно будет купить меньше товаров и услуг, чем прежде.

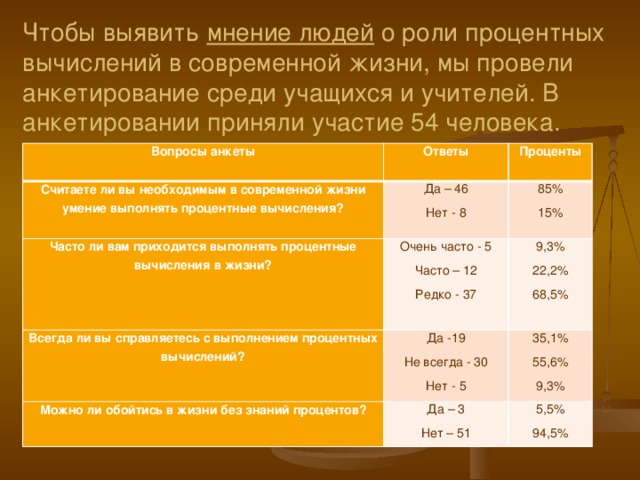
Для того, чтобы выявить мнение людей о роли процентных вычислений в современной жизни, мы провели анкетирование среди учащихся и учителей. В анкетировании приняли участие 54 человека.

94,5% опрошенных считают, что в жизни нельзя обойтись без знаний процентов. По результатам анкетирования можно сделать вывод о большой значимости процентов в жизни человека.

Заключение.

Проценты используются почти во всех сферах деятельности человека и с их помощью можно наглядно показать положительную или отрицательную динамику тех или иных процессов, протекающих в жизни общества. После проведения исследовательской работы я пришла к выводу, что современный человек очень тесно связан с процентами. Оказывается, проценты встречаются на работе, в школе, в магазинах, в аптеках на экранах телевизора и в периодической печати. Также люди пользуются процентами при оформлении кредитов или при вкладах сбережений в банк. Нельзя сегодня людям без знаний процентов! В ходе моей работы мне удалось достичь поставленной цели, выявить целесообразность применения процентов при решении повседневных задач. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся повседневной жизни постоянно. Встреча с людьми различных профессий показала, что все они сталкиваются с процентами. Задачи, которые им приходится решать, очень похожи на задачи в учебниках математики. Проценты – это одна из сложных тем математики, почти в каждом варианте тестовых заданий ОГЭ и ЕГЭ присутствует задача на проценты. Поэтому нужно как можно лучше знать и уметь пользоваться этой темой. Уметь грамотно и экономно проводить элементарные процентные вычисления должен каждый современный учащийся. Считаю, что моя работа найдет практическое применение на уроках алгебры, как пример решения задач разных видов с практическим содержанием, так и поможет увидеть широту возможных приложений математики, понять её роль в современной жизни. Список используемой литературы:

1. Ожегов С.И. Словарь русского языка: ОК. 57000 слов/Под ред.чл. – корр. АН СССР Н.Ю. Шведовой – 18 –е изд., стереотип – М.: Рус.яз., 1986 2. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. шк. – 5-е изд. – М.: Просвещение,1988 3. Алгебра. 9 класс : учеб. для образоват. организаций / [Ю.Н. Макарычев, НГ. Миндюк, К.И. Нешков, С.Б.Суворова]; под ред. С. А. Теляковского. –М. : Просвещение, 2014. 4. Математика 8-9 классы: сборник элективных курсов/авт.-сост. Сагателова Л.С., Студеницкая В.Н. -Волгоград:Учитель,2006. 5. ОГЭ. Математика: типовые экзаменационные варианты: 36 вариантов/ под ред.И.В. Ященко. – М.: Издательство «Национальное образование», 2015. 6. ОГЭ. Математика: типовые экзаменационные варианты: 36 вариантов/ под ред.И.В. Ященко. – М.: Издательство «Национальное образование», 2016. 7. Интернет.

Исследовательская работа по теме: « Практическое применение процентов в повседневной жизни »

Выполнила: ученица 9-го класса Власова Елена

Учитель математики: Клыкова Татьяна Алексеевна

2016 г.

В любом открытии есть 99 % труда и потения И только 1% таланта и способностей. Л.Магницкий

Цель: расширение и практическое применение знаний о вычислении процентов полученных на уроках алгебры.

Гипотеза  : Важна ли тема «Проценты» в жизни взрослых?

Задачи:

• При помощи специальной литературы и интернет изучить историю возникновения процентов.
• Рассмотреть основные задачи на применение процентов
• Показать применение процентов при решении реальных задач в различных сферах жизнедеятельности человека.
• Провести статистическое исследование
• Обобщить результаты. Сделать выводы.

Объектом исследования является комплекс задач на проценты

Предмет исследования – повседневное практическое использование математических вычислений поставленных задач с процентами

Актуальность и практическая значимость : необходимо повышать уровень знаний учащихся во время изучения процентов в школе, так как сейчас в вариантах ОГЭ и ЕГЭ встречаются задачи на проценты, и эти задачи очень часто вызывают затруднения. Во взрослой жизни во многих жизненных ситуациях люди обращаются к этой теме.

История возникновения процентов.

Слово «процент» происходит от латинского слова “pro centum”, что означает «со ста». Идея выражения частей целого постоянно в одних и тех же долях родилась ещё в древности у вавилонян, в их клинописных табличках уже содержались задачи на расчёт процентов. Были известны проценты и в Индии, где с давних пор вёлся счёт в десятичной системе счисления. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией.

В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять процен­ты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таб­лицы, которые составляли коммерческий секрет фирмы.

Знак «%» происходит, как полагают, от итальянского слова cento(сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения буквы t в наклонную черту произошёл современный символ для обозначения процента.

Другая версия происхождения этого знака заключается в том, что в Париже в 1685 году наборщик книги-руководства по коммерческой арифметике допустил опечатку – вместо cto написал %.

Виды задач на проценты и способы их решения.

• Нахождение процентного отношения двух чисел.
• Задача о нахождении процента от числа.
• Задача о нахождении числа по его процентам.
• Увеличение на р% 
• Уменьшение на р%

Нахождение процентного отношения двух чисел

Задача: Магазин делает пенсионерам скидку на определенное количество процентов от стоимости покупки. Сколько процентов составляет скидка, если буханка хлеба стоила в магазине 24 рубля, а пенсионер заплатил 21 рубль 12 копеек?

Решение:  1 рубль = 100 копеек. Значит, 21 рубль 12 копеек — это 21,12 рубля. Пенсионер заплатил за хлеб на 24−21,12=2,88 рубля меньше полной цены. Значит, скидка составила

2,8824⋅100%=12%

Ответ:  12%

Задача о нахождении числа по его процентам

Условие:   Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480 кг волокна?

Решение: Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т

Ответ: 2 т.

Уменьшение на p%

Условие: Спортивный магазин проводит акцию. Любой джемпер стоит 400 рублей. При покупке двух джемперов – скидка на второй джемпер 75%. Сколько рублей придется заплатить за покупку двух джемперов в период акции ? (№16 Вариант 1. ОГЭ-2016. Математика. Тип. тест. задания.ред. Ященко_2016 -80с)

Решение: Согласно условию задачи получается, что первый джемпер покупается за 100 % его исходной стоимости, а второй за 100 – 75 = 25 (%), т.е. всего покупатель должен заплатить 100 + 25 = 125 (%) от исходной стоимости. Далее можно рассмотреть решение тремя способами.

1 способ. 400 рублей принимаем за 100 %. Тогда в 1% содержится 400 : 100 = 4 (руб.), а в 125 % 4 • 125 = 500 (руб.)

Имеется еще 2 способа решения данной задачи.

Ответ: 500 рублей.

Решение более сложных задач на проценты

Условие: Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов? (Вариант 8 № 22. ОГЭ-2016. Математика. Тип. тест. задания_ред. Ященко_2016 - 80с)

Решение: Если в свежих фруктах содержится 75% воды, то сухого вещества будет 100 – 75 = 25 (%), а высушенные – 25%, то сухого вещества в них будет 100 – 25 = 75 (%).

При оформлении решения задачи, можно использовать таблицу:

Общая масса, кг   |   Концентрация сухого вещества   |   Масса сухого вещества

Свежие фрукты х 25% = 0,25 0,25 • х

Высушенные фрукты 45 75% = 0,75 0,75 • 45 = 33,75

Т.к. масса сухого вещества для свежих и высушенных фруктов не меняется, то получим уравнение:

0,25 • х = 33,75; х = 33,75 : 0,25; х = 135 (кг) – требуется свежих фруктов.

Ответ: 135 кг.

Правило креста

Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.

Данный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось.

Просто давался рецепт решения: либо рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.

Использование процентов людьми разных профессий

В энерго - сбытовой компании, рассматривают реализацию электроэнергии

Участок

Кигинский район

Товарная продажа

Салаватский район

5205

(тыс. рублей)

Сбор денежных средств

5255

Белокатайский район

11200

10700

100,96

%

6300

5200

1

Место

96

83

2

3

В профессии врача проценты тоже встречаются.

Рассмотрим Демографические показатели Кигинского района за 2006 - 2008г.г.(%)

Наименование

2006 год

рождаемость

Кигин.рн

2007 год

9,9

общая смертность

РБ

Кигин.р-н

10,1

млад, смертность

14,6

2008 год

14,4

26,6

РБ

ест. прирост

13,6

Кигин.р-н

10,9

12,7

13,9

-4,7

10,95

17,1

13,6

РБ

-2,5

0,5

14,1

9,8

13,5

6

13,8

-0,9

9,2

-0,3

-0,3

Распределение новорожденных по группам риска.

2006 год

Всего родилось в том числе:

абс.

2007 год

%

52

I группа риска

абс.

12

II группа риска

2008 год

58

%

III группа риска

23

9

абс.

14

17,3

IV группа риска

7

%

66

13,4

24,1

V группа риска

12

5

9

9,6

6

14

20,6

13

7

10,3

17,3

21,2

19,6

9

8

12

13,8

8

13,6

12,1

10

15,1

В нашей школе используют процентные вычисления в своей работе учителя

Класс

Кол-во

7

уч-ся

8

8

«5»

«4»

2

6

9

12

2

«3»

2

0

4

2

% успев

100

4

4

% качества

50

СОУ (%)

100

6

100

59

33,3

57,3

50

56

Помимо перечисленных немногих сфер жизнедеятельности, где можно встретить проценты, самой распространенной является, конечно, же банки .

Сегодня банки предлагают деньги в кредит на каждом шагу и практически любую вещь в магазине можно приобрести в рассрочку. Тех, кто берет в долг деньги в банке, называют заемщиками, а величину взятых у банка денег, называют кредитом. Кредит – ссуда, предоставление ценностей (денег, товаров) в долг. Популярность кредитования в нашей стране растет из года в год. Как показывает статистика, с 2001 года по 2016 год объем выдаваемых банками кредитов выросла в 95 раз. Огромный интерес физических лиц к разному роду кредитам вполне понятен, люди хотят упростить свою жизнь и жить лучше.

Вот какие преимущества дает кредитование:

• наконец-то вы можете приобрести то, о чем давно мечтали;
• в условиях инфляции кредитные ставки могут со временем оказаться заметно ниже роста цен, в этом случае можно даже сэкономить деньги;
• осуществив заветную покупку сегодня, через год можно радоваться, увидев заметный рост цен из-за инфляции;
• вы наберетесь опыта кредитования, что будет полезно вам в будущем;
• если в первый раз вы своевременно погасите проценты, то будете иметь положительную кредитную историю, что облегчить получение кредита в будущем.

Вывод: Я живу в России и считаю, что в данный момент для нас очень важно научиться грамотно пользоваться полезной услугой под названием «кредит» — уметь сравнивать доступные варианты и выбирать оптимальное предложение, разбираться в ценообразовании и не переплачивать лишнего.

Проценты в повседневной жизни.

Трудно найти область нашей жизни, где бы не применялись проценты. Как известно, выводы опираются на анализ. А самый удобный и быстрый способ анализировать – процентный. Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это даёт возможность упрощать расчёты и легко сравнивать части между собой и с целыми. В повседневной жизни мы постоянно сталкиваемся с процентами.

• Проценты на кухне
• Проценты в аптеке
• Проценты в магазине
• Проценты в банке
• Проценты и зарплата
• Проценты и пенсионеры
• Проценты и выборы

Проценты в повседневной жизни. Динамика численности населения

Численность населения Кигинского района по состоянию на 1 января 2017 года составила 17582 человека, численность населения по состоянию на 1 января 2016 года составила 18007 человека. За год численность населения уменьшилась на 2,36%. Согласно Всероссийской переписи населения 2010 года: татары — 51,4%, башкиры — 41,5%, русские — 5,6%, лица других национальностей — 1,5%

Проценты в повседневной жизни. Коммунальные услуги.  

Виды услуг

Тариф за январь 2016 года

Электроэнергия

1,79 р/кВт/ч

Тариф за декабрь 2016 года

Газ

% повышения

1,92 р /кВт/ч

4896,1 за 1000м 3

На 7,26%

4994,02 за 1000м 3

На 1,96%

Решение: Это легко считается по так называемому "правилу креста":

70     9      70% эссенция    \   /       9          нужная смесь    /   \  0     61     вода т. е. эссенцию и воду надо смешивать в соотношении 9:61, поэтому к 20 г эссенции нужно добавить 20·61/9 = 135,5 г воды

Чтобы выявить мнение людей о роли процентных вычислений в современной жизни, мы провели анкетирование среди учащихся и учителей. В анкетировании приняли участие 54 человека.

Вопросы анкеты

Ответы

Считаете ли вы необходимым в современной жизни умение выполнять процентные вычисления?

Часто ли вам приходится выполнять процентные вычисления в жизни?

Проценты

Да – 46

Нет - 8

Очень часто - 5

Всегда ли вы справляетесь с выполнением процентных вычислений?

85%

Часто – 12

Да -19

9,3%

Можно ли обойтись в жизни без знаний процентов?

15%

Да – 3

22,2%

Редко - 37

Не всегда - 30

35,1%

Нет – 51

Нет - 5

55,6%

68,5%

5,5%

94,5%

9,3%

.

94,5% опрошенных считают, что в жизни нельзя обойтись без знаний процентов. По результатам анкетирования можно сделать вывод о большой значимости процентов в жизни человека.

Проценты используются почти во всех сферах деятельности человека и с их помощью можно наглядно показать положительную или отрицательную динамику тех или иных процессов, протекающих в жизни общества. После проведения исследовательской работы я пришла к выводу, что современный человек очень тесно связан с процентами. Оказывается, проценты встречаются на работе, в школе, в магазинах, в аптеках на экранах телевизора и в периодической печати. Также люди пользуются процентами при оформлении кредитов или при вкладах сбережений в банк. Нельзя сегодня людям без знаний процентов!

Заключение.

Встреча с людьми различных профессий показала, что все они сталкиваются с процентами. Задачи, которые им приходится решать, очень похожи на задачи в учебниках математики. Проценты – это одна из сложных тем математики, почти в каждом варианте тестовых заданий ОГЭ и ЕГЭ присутствует задача на проценты. Поэтому нужно как можно лучше знать и уметь пользоваться этой темой. Уметь грамотно и экономно проводить элементарные процентные вычисления должен каждый современный учащийся. Считаю, что моя работа найдет практическое применение на уроках алгебры, как пример решения задач разных видов с практическим содержанием, так и поможет увидеть широту возможных приложений математики, понять её роль в современной жизни.

Спасибо за внимание!!!