Исследовательская работа "Простейшие статистические характеристики"

40

Министерство образования РБ

Отдел образования

администрации муниципального района

Янаульский район

Исследовательская работа по математике

«Простейшие статистические характеристики»

Работа ученицы 7 класса МБОУ СОШ с. Шудек Менгафаровой Елены Вадимовны.

Руководитель: Мухаметзянова Ангелина Виталиевна – учитель математики I квалификационной категории.

Шудек

Содержание

1. Введение………………………………………………………..стр. 3

2. Среднее арифметическое, размах и мода ………………..…стр. 4-7

3. Медиана как статистическая характеристика ……………...стр.8-13

4. Заключение………………………………………………….…стр. 14

5. Использованная литература…………………………………..стр. 15

6. Приложение 1 (Условия задач)…...……………………...…..стр. 16-20

7. Приложение 2 (Решение задач)..…………………………….стр. 21-29

8. Приложение 3 (Условия задач, составленные собой)…......стр. 30-33

9. Приложение 2 (Решение своих задач)..…………………….стр. 34-37

Введение

На уроке алгебры в 7 классе мы ознакомились с простейшими статистическими характеристиками, такими как среднее арифметическое, размах, мода и медиана. Мы могли найти данные характеристики только в несложных доступных примерах. Статистические характеристики для любых рядов, диапазонов можно найти и с помощью компьютера. То есть повторяется старый материал, но на новой основе.

Теоретический материал и условия задач взяты из [1]. Только в данной работе тот изученный материал «предложен» на Excel, с тем чтобы показать учащимся другие способы решения статистических задач, освободив их от рутинных вычислений.

Особое внимание уделяется демонстрации оптимизационных задач, решаемых в табличном процессе Excel.

Исследовательская работа обеспечивает:

- межпредметные связи математики с информатикой дают возможность изучать некоторые разделы математики с помощью компьютера;

- приобретение навыков работы в табличном процессе Excel;

- приобретение навыков работы в редакторе формул.

Выполняя исследовательскую работу, решается и такая важная задача, как формирование умений и способов деятельности для решения практических задач из экономики, статистики.

В данной работе показывается, как решать задачи статистики с помощью Excel на основе встроенных функций. Все представленные задачи имеют очень простую структуру и не требуют от учащихся глубоких знаний Excel.

Среднее арифметическое, размах и мода

При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и сумму разделить на 12.

Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Мы нашли, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем по 27 минут. Проводя аналогичные наблюдения за этой группой учащихся, можно проследить, какова была средняя затрата времени на выполнение домашнего задания по алгебре в течение недели, сравнить среднюю затрату времени на выполнение в какой-либо день домашних заданий по алгебре и русскому языку и т.п. Заметим, что для серьезных выводов о загруженности учащихся домашними заданиями необходимо выделить для наблюдений значительно большую группу, чем 12 человек.

Обычно среднее арифметическое находят тогда, когда
хотят определить среднее значение для некоторого ряда данных.

Среднее арифметическое представляет собой то значение величины, которое получается, когда сумма всех наблюдаемых значений мысленно распределяется поровну между единицами наблюдения. Например, вычислив среднее арифметическое удоев молока, полученных за сутки на ферме от всех коров, мы найдем тот удой, который получили бы на ферме в эти сутки от одной коров, если бы все коровы давали одинаковое количества молока, т.е. найдем среднесуточный удой молока на ферме от одной коровы. Аналогично находят среднюю урожайность пшеницы с 1 га в районе, среднюю выработку рабочего бригады за смену и т.п.

Заметим, что иногда вычисление среднего арифметического не дает полезной информации. Например, лишено смысла нахождение средней температуры больных в госпитале, среднего размера обуви, которую носят учащиеся школы.

В рассмотренном примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 минут. Однако анализ приведенного ряда данных показывает, что время, затраченное некоторыми учащимся, существенно отличается от 27 минут, т.е. от среднего арифметического. Наибольший расход равен 37 минут, а наименьший – 18 минут. Разность между наибольшим и наименьшим расход времени составляет 19 минут. В этом случае говорят, что размах ряда равен 19.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда находят тогда, когда хотят определить как велик разброс данных в ряду. Пусть, например, в течение суток отмечали каждый час температуру воздуха в городе. Для полученного ряда данных полезно не только вычислить среднее арифметическое, показывающее, какова среднесуточная температура, но и найти размах ряда, характеризующий колебание температуры воздуха в течение этих суток.

При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группу учащихся, т.е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 – мода рассматриваемого ряда.

Модой ряда чисел называется, число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моду совсем. Например, в ряду чисел: 47, 46, 50, 52, 47, 52, 49, 45, 43, 53, 53, 47, 52

две моды – это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа – менее трех раз.

В ряду чисел: 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.

Моду ряда данных обычно находят тогда, когда хотят выявить некоторый типичный показатель. Например, если изучаются данные о размерах мужских сорочек, проданных в определенный день в универмаге, то удобно воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом. Мода является наиболее приемлемым показателем при выявлении расфасовки товара, которой отдают предпочтение покупатели; цены на товар данного вида, распространенной на рынке, и т.п.

Рассмотрим еще пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:

36, 35, 35, 36, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.

Найдем для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т.е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим

35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.

Вычислим среднее арифметическое:

Размах ряда равен 39-35=4. Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.

Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит 4 деталей; типичной является выработка, равная 36 деталям.

Среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда, а мода, если она существует, обязательно совпадает с двумя или более числами ряда. Кроме того, в отличие от среднего арифметического понятие «мода» относится не только к числовым данным. Модой будут служить и те ответы учащихся, которые встречаются чаще всего при ответе на 1 и тот же вопрос.. Этим и объясняется само название «мода».

Такие характеристики, как среднее арифметическое, размах и мода, находят применение в статистике – науке, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т.п. Результаты статистических исследований широко используются для практических и научных выводов.

Медиана как статистическая характеристика

Рассмотрим ещё одну статистическую характеристику.

Начнем с примера. В таблице указан расход электроэнергии в январе жильцами девяти квартир:

Номер квартиры	1 1	2 2	3 3	4 4	5 5	6 6	7 7	8 8	9 9
Расход электроэнергии, кВт. Ч	85	64	78	93	72	91	1 72	75	82

Составим из данных, приведенных в таблице, упорядоченный ряд:

64, 72, 72, 75, 78, 82, 85, 91, 93.

В полученном упорядоченном ряду 9 чисел. Нетрудно заметить, что в середине ряда расположено число 78: слева от него записано четыре числа и справа четыре числа. Говорят, число 78 является срединным числом, или, иначе медианой, рассматриваемого упорядоченного ряда чисел (от латинского слова mediana, которое означает «среднее»). Это число считают также медианой исходного ряда данных.

Приведем теперь другой пример. Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам добавили ещё десятую. Получим такую таблицу:

Номер квартиры	1 1	2 2	3 3	4 4	5 5	6 6	7 7	8 8	9 9	10
Расход электроэнергии, кВт. Ч	85	64	78	93	72	91	1 72	75	82	883

Так же как в первом случае, представим полученные данные в виде упорядоченного ряда чисел: 64, 72, 72, 75, 78, 82, 83, 85, 91, 93.

В этом числовом ряду четное число членов и имеются два числа, расположенные в середине ряда: 78, 82. Найдем среднее арифметическое этих чисел: .

Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы - слева от него находятся пять членов ряда и справа тоже пять членов ряда:

80

64, 72, 72, 75, 78, 82, 83, 85, 91, 93.

Говорят, что медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Если в упорядоченном числовом ряду содержится 2n-1 членов, то медианой ряда является n-й член, так как n-1 членов стоит до n-го члена и n-1 членов - после n-го члена. Если в упорядоченном числовом ряду содержится 2n членов, то медианой является среднее арифметическое членов, стоящих на n-м и n+1-м местах.

В каждом из рассмотренных выше примеров, определив медиану, мы можем указать номера квартир, для которых расход электроэнергии жильцами превосходит срединное значение, т.е. медиану.

Рассмотрим ещё один пример. Известно, что 34 сотрудника отдела приобрели акции некоторого акционерного общества. Данные о числе акций, приобретенных сотрудниками, представлены в виде следующего упорядоченного ряда:

2, 2, 2, 2, 2, 3 , 3,…, 3, 4 , 4,…4, 100.

12 раз 16 раз

Найдем медиану этого ряда. Так как всего в ряду 34 числа, то медиана равна среднему арифметическому 17-го и 18-го членов, т.е. равна (3+4)/2=3,5.

Вычисляя среднее арифметическое этого ряда, найдем, что оно приближенно равно 6,2, т.е. в среднем сотрудники отдела приобрели примерно по 6 акций.

Мы видим, что в данном случае медиана лучше отражает реальную ситуацию, так как половину всех сотрудников составляют те, которые приобрели не более 3 акций.

Вообще среднее арифметическое зависит от значений всех членов в упорядоченном ряду данных, в том числе и от значений крайних членов, которые часто бывают наименее характерными для рассматриваемой совокупности данных. Поэтому при анализе данных сведения о среднем арифметическом часто дополняются указанием медианы.

Такие показатели, как среднее арифметическое, мода и медиана, по-разному характеризуют данные, полученные в результате наблюдений. Поэтому на практике при анализе данных в зависимости от конкретной ситуации используют какой-либо из этих показателей, либо два из них, либо даже все три.

Если, например, анализируются сведения о годовых доходах нескольких туристических фирм города, го удобно использовать все три показателя. Среднее арифметическое покажет средний годовой доход фирм, мода будет характеризовать типичный показатель годового дохода, медиана позволит определить туристические фирмы, годовой доход которых выше или ниже срединного показателя.

При анализе результатов, показанных участницами заплыва на дистанцию 100 м, наиболее приемлемой характеристикой является медиана. Знание медианы позволит выделить для участия в соревнованиях группу спортсменок, показавших результат выше срединного. Как видно из вышеизложенного, медиану находить достаточно сложно, но у нас имеется табличный процессор Ехсеl, в котором есть встроенная функция МЕДИАНА.

Пример. Найдите среднее арифметическое, размах, медиану и моду ряда чисел:

А	24	22	27	20	16	31
Б	11	9	7	6	2	0	1
В	30	5	23	5	28	30
Г	144	146	114	138

Технология работы:

- запустить табличный процессор Excel.

- заполнить таблицу в соответствии с образцом:

	А	B	C	D	E
1		Исходные данные
2	1	24	11	30	144
3	2	22	9	5	146
4	3	27	7	23	114
5	4	20	6	5	138
6	5	16	2	28
7	6	31	0	30
8	7		1
9
10
11
12
13	Результаты
14	Мин	Формула 1	Заполнить вправо
15	Макс	Формула 2	Заполнить вправо
16	Срзнач	Формула 3	Заполнить вправо
17	Размах	Формула 4	Заполнить вправо
18	Медиана	Формула 5	Заполнить вправо
19	Мода	Формула 6	Заполнить вправо

• Ввести формулы в расчетные ячейки:

Ячейка	Формула
В14	=МИН(В2:В8)
В15	=МАКС(В2:В8)
В16	=СРЗНАЧ(В2:В8)
В17	=В15- В14
В18	=МЕДИАНА(В2:В8)
В19	=МоДА(В2:В8)

1. Для создания формул выполняем следующие действия:

• щелкнуть по кнопке “мастер функций f_x”;

• выбрать Статистические и далее МИН, МАКС, или Срзнач, Медиана, Мода и нажать ОК;

• указать диапазон клеток;

• нажмите ОК.

2) Для нахождения размаха чисел необходимо в свободной ячейке создать формулу, находящую разность. Для этого:

- наберите на клавиатуре знак «=»;

- введите адрес ячейки, содержащей значение МАКС (т. е. В15);

- наберите на клавиатуре знак «-»;

- введите адрес ячейки, содержащей значение МИН (т. е. В 14);

- нажмите «Еnter».

3) Для заполнения вправо выделим диапазон В14:В17. Подведем указатель мыши к правому нижнему углу выделенного диапазона и протянем вправо.

4) скопируйте этот лист (у вас появится копия этого листа в нижней части Книги), выполните команду: Сервис - Параметры и на вкладке Вид поставьте флажок в Параметрах окна рядом с Формулы.

Заключение

На уроке алгебры мы ознакомились с простейшими статистическими характеристиками, такими как среднее арифметическое, размах, мода и медиана. Но мы могли найти данные характеристики только в несложных доступных примерах. Статистические характеристики для любых рядов, диапазонов я научилась находить с помощью компьютера, используя табличный процессор Excel.

При выполнении данной работы все задачи, предложенные в учебнике для 7 класса, я решила на компьютере. Для этого все задачи я сохранила в Книге «Задачи», где каждому листу соответствовало решение одного номера из учебника. Но для удобства и наглядности, на каждый номер было решено выделить два листа этой Книги: на первом листе – задача решена и видны только результаты вычислений, а во второй – только использованные формулы. Т.е. я особое внимание уделила демонстрации задач, решаемых в табличном процессе Excel.

Выполнив эту исследовательскую работу я научилась и приобрела навыки работы в табличном процессе Excel (использовать встроенные функции) и в редакторе формул (правильно записывать дробные выражения).

Использованная литература:

1. Алгебра: учеб. для 7 кл. общеобразоват. учреждений /[Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Мешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 16-е изд. – М.: Просвещение, 2007.- 240 с.: ил.

2. Макарычев Ю. В., Миндюк Н. Г. Элементы статистики и теории вероятностей. – М.: Просвещение, 2003

3. Информатика и ИКТ. Базовый курс: Учебники для 8 класса / Н. Д. Угринович. – 5-е изд. – М.: БИНОМ. Лаборатория знаний, 2007.- 205 с.: ил.

Приложение 1

Условия задач

Упражнения из учебника [1]

167. Найдите среднее арифметическое и размах ряда чисел:

а) 24, 22, 27, 20, 16, 31; 6) 30, 5, 23, 5, 28, 30.

168. Найдите среднее арифметическое, размах и моду ряда чисел:

а) 32, 26, 18, 26, 15, 21, 26;

6) 21, 18,5, 25,3, 18,5, 17,9;

в) 67,1, 68,2, 67,1, 70,4, 68,2;

г) 0,6, 0,8, 0,5, 0,9, 1,1.

169. Найдите среднее арифметическое, размах и моду ряда чисел:

а) 16, 22, 16, 13, 20, 17;

6) -21, -33, -35, -19, -20, -22;

в) 61, 64, 64, 83, 61, 71, 70;

г) -4, -6, 0, 4, 0, 6, 8, -12.

170. Как могут измениться размах и мода ряда чисел, если:

а) дополнить его числом, превосходящим все остальные;

б) вычеркнуть из него число, меньшее всех остальных;

в) дополнить его числом, равным наибольшему из чисел?

171. В таблице показан расход электроэнергии некоторой семьей в течение года:

Найдите средний ежемесячный расход электроэнергии этой семьей.

172. В таблице приведены данные о продаже в течение недели картофеля, завезенного в овощную палатку:

Сколько картофели в среднем продавали ежедневно в эту неделю?

173. Среднее арифметическое ряда, состоящего из десяти чисел, равно 15. К этому ряду приписали число 37. Чему равно среднее арифметическое нового ряда чисел?

174. Среднее арифметическое ряда, состоящего из девяти чисел, равно 13. Из этого ряда вычеркнули число 3. Чему равно среднее арифметическое нового ряда чисел?

175. В ряду чисел 2, 7, 10,___, 18, 19, 27 одно число оказалось стертым. Восстановите его, зная, что среднее арифметическое этих чисел равно 14.

176. В ряду чисел 3, 8, 15, 30, _, 24 пропущено одно число. Найдите его, если:

а) среднее арифметическое ряда равно 18;

б) размах ряда равен 40;

в) мода ряда равна 24.

177. В таблице показано число деталей, изготовленных за смену рабочими одной бригады:

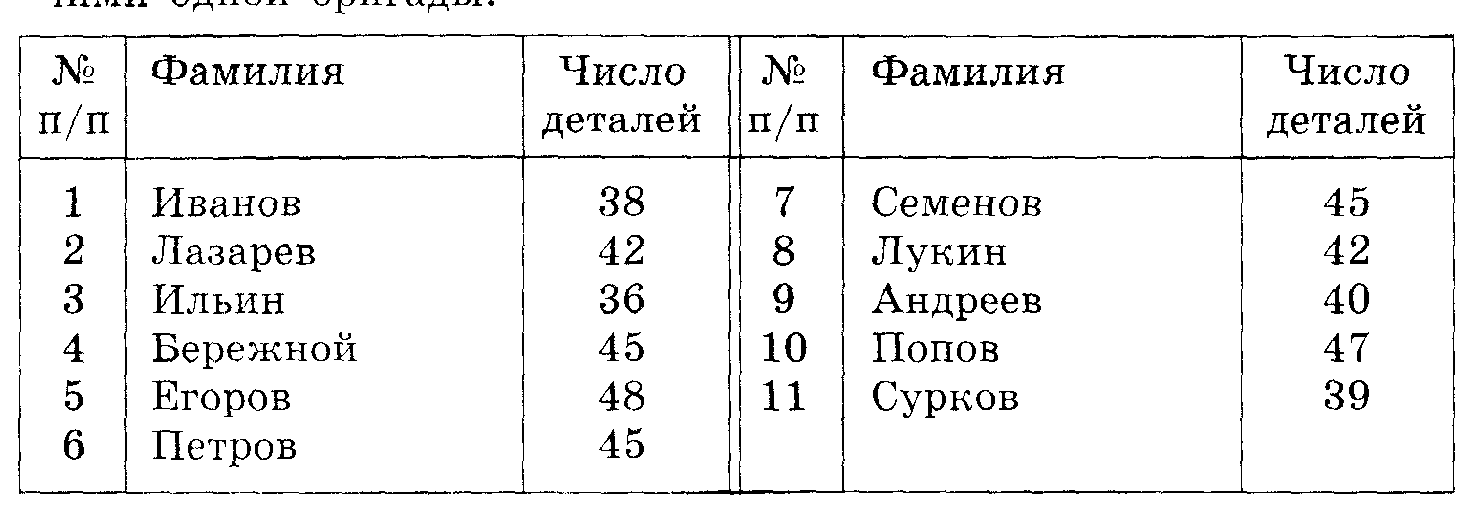
Для представленного в таблице ряда чисел найдите среднее арифметическое, размах и моду. Каков смысл каждого из этих показателей?

178. На соревнованиях по фигурному катанию выступление спортсмена было оценено следующими баллами:

5,2, 5,4, 5,5, 5,4, 5,1, 5,1, 5,4, 5,5, 5,3.

Для полученного ряда чисел найдите среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?

179. В аттестате о среднем образовании у четырех друзей — выпускников школы — оказались следующие оценки:

Ильин: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;

Семенов: 3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;

Попов: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;

Романов: 3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4.

С каким средним баллом окончил школу каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характеристики вы использовали при ответе?

180. В фермерском хозяйстве отведены под пшеницу три участка, площади которых равны 12 га, 8 га и б га. Средняя урожайность на первом участке составляет 18 ц с 1 га, на втором - 19 ц с 1 га, на третьем — 23 ц с 1 га. Чему равна средняя урожайность пшеницы в этом хозяйстве? Можно ли найти среднюю урожайность пшеницы (в центнерах), вычислив среднее арифметическое чисел 18, 19 и 23?

181. Проведи учет числа бракованных деталей в 10 ящиках с одинаковым числом деталей, получили следующий ряд данных: 1, 2, 2, 3, 1, 0, 2, 1, 3, 2.

Найдите для этого ряда среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?

182. Каждый из 24 участников соревнований по стрельбе произвел по десять выстрелов. Отмечая всякий раз число попаданий в цель, получили следующий ряд данных:

6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9, 7, 7, 9, 8, 6, 6, 5, 6, 4, 3, 6, 5.

Найдите для этого ряда размах и моду. Что характеризует каждый из этих показателей?

183. В таблице записаны результаты ежедневного измерения на метеостанции в полдень температуры воздуха (в градусах Цельсия) в течение первой декады марта:

Число месяца	1	2	3	4	5	6	7	8	9	10
Температура,	-2	-1	-3	0	1	2	2	3	4	3

Найдите среднюю температуру в полдень в эту декаду. Составьте таблицу отклонений от средней температуры воздуха в полдень в каждый из дней декады.

186. Найдите медиану ряда чисел:

а) 30, 32, 37, 40, 41, 42, 45, 49, 52;

6) 102, 104, 205, 207, 327, 408, 417;

в) 16, 18, 20, 22, 24, 26;

г) 1,2, 1,4, 2,2, 2,6, 3,2, 3,8, 4,4, 5,6.

187. Найдите среднее арифметическое и медиану ряда чисел:

а) 3,8, 7,2, 6,4, 6,8, 7,2; б) 21,6, 37,3, 16,4, 12,6.

188. Известно, что ряд данных состоит из натуральных чисел. Может ли для этого ряда быть дробным числом:

189. В таблице показано число изделий, изготовленных за месяц членами бригады:

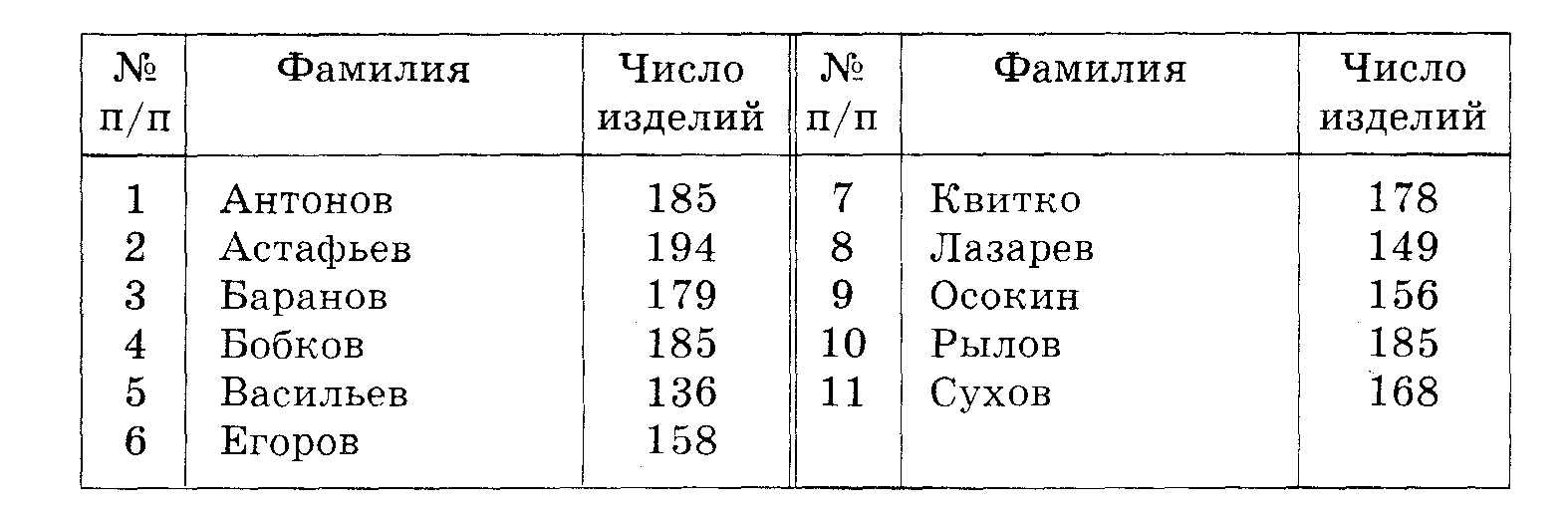
Найдите медиану этого ряда данных. У кого из членов бригады выработка за месяц была больше медианы?

190. В таблице показано, сколько акций одинаковой стоимости некоторого акционерного общества приобрели сотрудники отдела:

Найдите медиану этого ряда данных. У кого из сотрудников отдела число приобретенных акций не превосходит медиану?

191. Подсчитав число сорных семян в 15 пакетиках с семенами, получили такие данные:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1.

Для представленного ряда данных найдите среднее арифметическое и медиану. Что характеризует каждый из этих показателей?

192. Отмечая время (с точностью до минуты), которое токари бригады затратили на обработку одной детали, получили такой ряд данных:

30, 32, 32, 38, 36, 31, 32, 38, 35, 36,

32, 40, 42, 36, 33, 35, 32, 32, 40, 38.

для полученного ряда данных найдите размах, моду и медиану. Объясните практический смысл этих статистических показателей.

193. В организации вели ежедневный учет поступивших в течение месяца писем. В результате получили такой ряд данных:

39, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 25,

34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 32.

Для полученного ряда данных найдите среднее арифметическое, размах, моду и медиану. Каков практический смысл этих показателей?

Приложение 2.

Решение задач.

№167

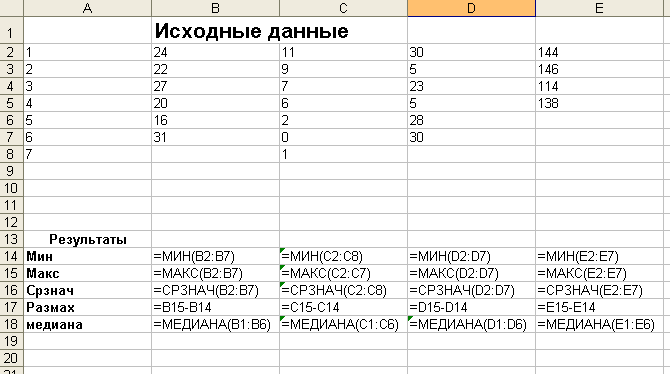
№ 168

№ 169

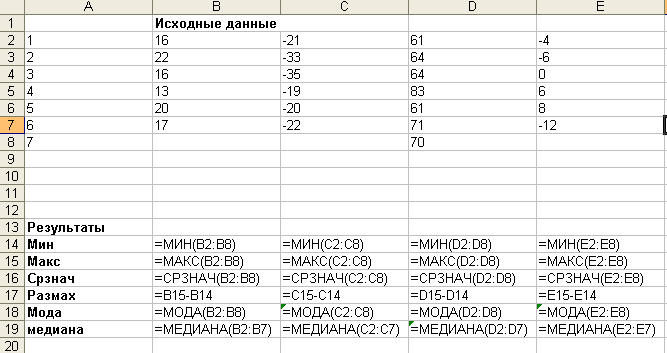
№ 170

а)размах увеличивается, а мода не меняется

б) размах уменьшается, а мода не меняется

в) размах не меняется, а модой станет то дополненное число.

№ 171

№ 172

№173

1.Найдём сумму чисел первоначального ряда:

х= 15*10=150

2.Найдём сумму чисел нового ряда:

у=150+37=187

3.Найдём количество чисел в новом ряду:

10+1=11

4. Найдем среднее арифметическое нового ряда чисел:

187:11=17

Ответ: среднее арифметическое нового ряда чисел равно 17.

№174

1.Найдём сумму чисел первоначального ряда:

Х= 13*9=117

2.Найдём сумму чисел нового ряда:

У=117-3=114

3.Найдём количество чисел в новом ряду:

9-1=8

4. Найдем среднее арифметическое нового ряда чисел:

114:8=14,25

Ответ: среднее арифметическое нового ряда чисел равно 14,25.

№175

Решение:

(2+7+10+х+18+19+27):7=14

(83+х):7=14

83+х =14*7

83+х=98

х=98-83

х=15

Ответ: 15.

№176

а) (3+8+15+30+х+24):6=18

(80+х):6=18

80+х=18*6

80+х=108

х=28

Ответ: 28.

б) 1 случай: пусть наибольшее число - у;

наименьшее число - 3;

размах - 40, тогда:

у-3=40

у=40+3

у=43

2 случай: пусть

наибольшее число - 30;

наименьшее число - у;

размах - 40, тогда:

30-у=40

у=30-40

у=-10

Ответ: -10 или 43

в) т.к. мода ряда равна 24, а в заданном ряду чисел нет повторяющихся, то пропущенное число – 24.

Ответ: 24

№ 177

№ 178

№ 179

№ 180

2 способ:

(12*18+8*19+6*23):(12+8+6)=(216+152+138):26=506:26=19,5 (ц/га)

№ 181

№ 182

№ 183

№185-186 – задания не по статистике

№ 186

№187

№188

а) Да, может.

б) Нет

в) Нет

г) Да, может.

№ 189

№ 190

№ 191

№ 192

№ 193

Приложение 3

Условия задач, составленные самой

№1 В 10 классе МБОУ СОШ с..Шудек 5 учащихся. За 1 полугодие 2009-2010 учебного года оценки у них оказались такими:

Ф.И. О.	Оценки
Апсаликова	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5
Валиева	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5
Калимуллин	3	4	4	4	4	3	4	4	4	4	5	5	4	4	4	4	4	5	4
Сайфиева	3	4	4	3	3	3	3	4	3	3	4	4	3	3	3	3	4	4	4
Хайдарова	3	3	4	3	3	3	3	4	3	3	4	4	3	3	3	3	4	4	4

Определить среднюю оценку каждого из учащегося. Указать наиболее типичную для каждого из них оценку.

№2 В таблице указана оплата за газ за 2009 год семьи Менгафаровых:

Месяц	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Оплата, руб.	735,28	722,84	722,84	722,84	722,84	722,84	830,96	830,96	865,93	865,93	865,93	865,93

Для этого ряда найдите среднее арифметическое и моду? Каков практический смысл этих показателей?

№3 В таблице приведены данные о потреблении картофеля в течение одной из недель в столовой МБОУ СОШ. С.Шудек в 2009-2010 уч. году:

День недели	Понедель-ник	Вторник	Среда	Четверг	Пятница	Суббота
Количество картофеля, кг	2	14	2	52	12	0

Сколько картофеля в среднем употреблялось ежедневно в эту неделю?

№4 В таблице записаны результаты измерения температуры воздуха в течении одной из суток января.

Часы	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
Темп -ература, 0С	-32	-32	-32	-32	-32	-32	-32	-33	-34	-30	-30	-28	-27	-20	-23	-23	-24	-24	-26	-28	-29	-31	-33	-35

Определите среднесуточную температуры воздуха за эти сутки?

№5. В 4 квартале 2009 года еженедельно в адрес МБОУ СОШ.с.Шудек приходили письма. В результате получили такой ряд:

№ недели	1	2	3	4	5	6	7	8	9	10	11	12	13
Кол-во писем	11	11	9	22	9	17	17	25	21	16	21	37	14

Для полученного ряда данных найдите среднее арифметическое, размах, моду и медиану. Каков практический смысл этих показателей?

№6. Качество успеваемости по классам в МБОУ СОШ с. Шудек за 1 полугодие 2005-2010 уч. года составляет по классам

Кл.	2	3	4	5	6	7	8	9	10	11
Успеваемость	66%	60%	50%	30%	50%	50%	47%	40%	40%	14.3%

Определить среднюю успеваемость по школе

№7. По результатам подсчета пропущенных уроков учащимися 7 класса была составлена следующая таблица.

№	Ф. И. О.	Кол-во проп. ур.	№	Ф. И. О.	Кол-во проп. ур.
1	Апсаликов А.	5	8	Менгафарова Е.	13
2	Ахметов Т.	17	9	Семенова А.	0
3	Баширова О.	16	10	Семенова С.	17
4	Баширов К.	10	11	Тимирзянова Д.	16
5	Васиулинна К.	11	12	Тимирзянова Я.	16
6	Волкова Н.	16	13	Хайретдинова В.	10
7	Гарипова В.	11	14	Шайдуллин Д.	17

Найдите медиану этого ряда данных. У кого из учащихся число пропущенных уроков не превосходит медиану?

№8. Из возрастов учителей МБОУ СОШ села Шудек составлен следующий ряд данных: 35, 51 ,40, 21, 56, 25, 28, 56, 42, 30, 55, 28, 43, 57, 57, 32, 55, 53, 31, 48, 35, 26, 27, 28. Для полученного ряда данных найдите среднее арифметическое, размах, моду и медиану. Каков смысл этих показателей?

№9. В таблице указаны показатели прыжка в длину с места учащихся восьмого класса .

№	ФИО	Длина прыжка, м	№	ФИО	Длина прыжка
1	Ахматуллин Г	2,26	10	Камалетдинова С	1,80
2	Ахматуллин т	2,31	11	Нурисламов Я	2,05
3	Ахметов А	2,05	12	Сайфутдинов К	2,05
4	Гарипова К	1,92	13	Семенова А	1,80
5	Гатаулинна Э	1,86	14	Хаерзаманов Л	2,35
6	Зайнетдинова Н	1,80	15	Хайретдинова М	1,89
7	Идиятов Д	2,00	16	Чалгубаева А	1,88
8	Идиятова И	1,75	17	Шараев В	2,10
9	Камалетдинов О	1,90

Определите моду и среднюю длину прыжка?

№10. Количественный состав учащихся МБОУ СОШ с. Шудек в 2009-2010году представлен в таблице.

Класс	1	2	3	4	5	6	7	8	9	10	11
Кол-во учащихся	2	6	5	10	10	16	14	17	15	5	7

Определите средний показатель количества детей в классах. Каков практический смысл моды, медианы для этого класса? Определите их.

Приложение 4

Решение своих задач

№1

№2

№3

№4

№5

№6

№7

№8

№9

№10