
Открытая конференция творческих работ школьников «Малые грани»
Линейная функция
в природе и в технике
Выполнил:
Унжаков Владислав,
ученик 7 – Д класса МАОУ «Центр образования № 13
имени Героя Советского Союза Н.А.Кузнецова»,
г. Тамбов

Актуальность исследования
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.
А.Н.Крылов
А.Н.Крылов
Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими.
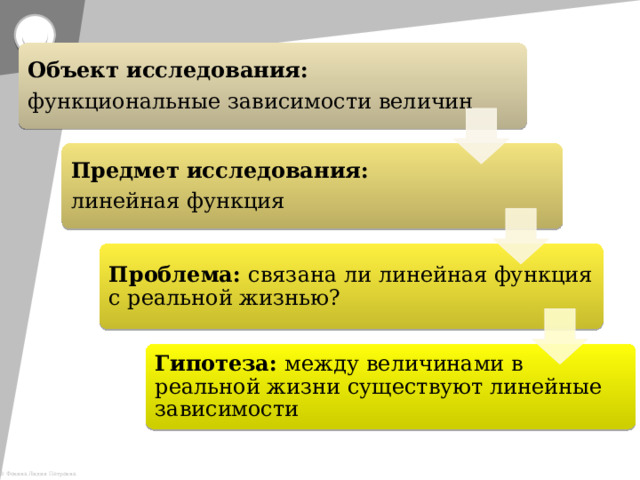
Объект исследования:
функциональные зависимости величин
Предмет исследования:
линейная функция
Проблема: связана ли линейная функция с реальной жизнью?
Гипотеза: между величинами в реальной жизни существуют линейные зависимости

Цель исследования: найти доказательства применения линейной функции в реальной жизни
Задачи исследования:
- Изучить историю возникновения понятия «функция»
- Обобщить материал по теме «Линейная функция»
- Найти примеры линейных функций в окружающем мире
- Провести микроисследование по выявлению линейных зависимостей вокруг нас

Этапы работы над проектом: I. Теоретический II. Практический III. Обобщающий
Методы исследования:
поиск информации, анализ, сравнение, сопоставление, обобщение, опыт, наблюдение.
Новизна работы: поиск на практике подтверждения существования линейной зависимости между величинами

Теоретический этап
Историческая справка
XVII век
Франсуа Виет и Рене Декард ввели е диную буквенную математическую символику
1671 год Исаак Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени
1673 год Готфрид Лейбниц впервые употребил слово “функция”
1748 год Леонард Эйлер окончательно сформулировал понятие функции с аналитической точки зрения

Теоретический этап
Что такое функция?
Функция - это зависимость переменной у от переменной х, при которой каждому значению переменной х ставится в соответствие единственное значение переменной у.
х – независимая переменная (аргумент)
у – зависимая переменная (значение функции)
Теоретический этап
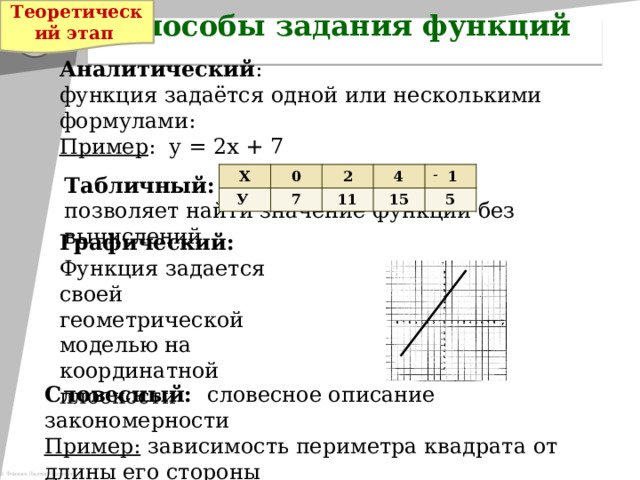
Способы задания функций
Аналитический :
функция задаётся одной или несколькими формулами:
Пример : у = 2х + 7
Х
0
У
7
2
4
11
15
5
Табличный:
позволяет найти значение функции без вычислений
Графический:
Функция задается своей геометрической моделью на координатной плоскости
Словесный: словесное описание закономерности
Пример: зависимость периметра квадрата от длины его стороны
 0 к Возрастает Убывает Постоянная " width="640"
0 к Возрастает Убывает Постоянная " width="640"
Теоретический этап
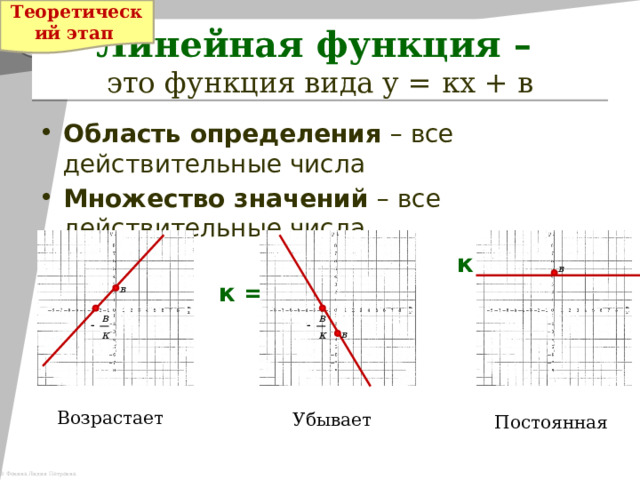
Линейная функция – это функция вида у = кх + в
- Область определения – все действительные числа
- Множество значений – все действительные числа
к0 к
Возрастает
Убывает
Постоянная

Практический этап
Линейные зависимости в математике
- Зависимость длины окружности
от ее радиуса:
С = 2πR
R
2) Зависимость между градусными мерами смежных углов:
у = 180° - х
х
у
3) Зависимость периметра
квадрата от длины его стороны
Р = 4а

Практический этап
Линейные зависимости в физике
- Зависимость координаты точки при прямолинейном равномерном движения от времени:
x(t) = vt +
2) Зависимость давления жидкости на дно сосуда от высоты столба жидкости:
P = ⍴ɡh
3) Зависимость длины рельсов от температуры
L =L 0 (1+αt) формула теплового расширения твёрдых тел

Практический этап
Линейные зависимости в биологии
- Зависимость скорости роста гриба от времени:
l=l 0 +5t , гдеl – длина гриба (мм), l 0 – первоначальная длина (мм), t – время (мин).
2) Зависимость количества сине-зеленых водорослей от количества фосфора в воде: р=0,983р+50,6 , где а – численность сине-зелёных водорослей, р – концентрация общего фосфора.

Практический этап
Линейные зависимости в литературе
Пословица
Математическая интерпретация
Чем дальше в лес, тем больше дров
у = кх + в
Без труда не вытащишь и рыбку из пруда
у= кх
Как аукнется, так и откликнется
Зависимость количества дров от
расстояния от края леса
Зависимость количества выловленной
у= кх
Долго думал, да ничего не выдумал
у = 0
рыбы от приложенных трудовых затрат
Зависимость добрых дел, которые
Зависимость полезных мыслей от
совершают люди для тебя, от добрых
времени, затраченного на их появление
дел, которые ты совершаешь для людей

Практический этап
Линейные зависимости вокруг нас (результаты микроисследования)
Вопрос: Как зависит стоимость доставки
крупногабаритного товара от этажности дома?
Условия доставки:
до подъезда - 350 руб, на этаж – 100 руб
х – этаж, на который надо донести груз
у – стоимость всей доставки
Формула: у = 350 + 100х
х
у
1
450
2
550
3
650
6
950
8
10
1150
1350
Вывод: зависимость стоимости доставки товара на этаж от числа этажей - линейная

Практический этап
Линейные зависимости вокруг нас (результаты микроисследования)
Вопрос: Как зависит калорийность молочного продукта от его жирности? (на примере кефира)
Жирность
х (%)
Калорийность
0
у (ккал)
31
1,5
41
2,5
52
3,2
58
3,5
61
6
85
у = 9х + 31
Вывод: зависимость стоимости калорийности кефира от его жирности - приближается к линейной

Обобщающий этап
Познакомились с определением понятия «функция» и способами задания функции
Обобщили сведения о линейной функции, выяснили её связь с повседневной жизнью
Научились устанавливать функциональные зависимости между величинами
Заключение

Обобщающий этап
Выводы
Можно найти связь математики с реальным миром при изучении любой темы
В окружающем мире есть величины, связанные друг с другом линейными зависимостями
Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими

Использованные источники
- Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.
- Волович М.Б. «Справочник школьника 5-11 класс»
- Макарычев Ю.Н. “Алгебра 7 класс”. – 6-е изд. – М. : Издательство “Просвещение”, 1998.
- Мордкович А.Г. “Алгебра 7 класс”. – 11-е изд. – М. : Издательство “Мнемозина”, 2008.
- Интернет-ресурсы:
http://linear function.ru
http://ru.wikipedia.org/wiki/ЭТ















 0 к Возрастает Убывает Постоянная " width="640"
0 к Возрастает Убывает Постоянная " width="640"



















