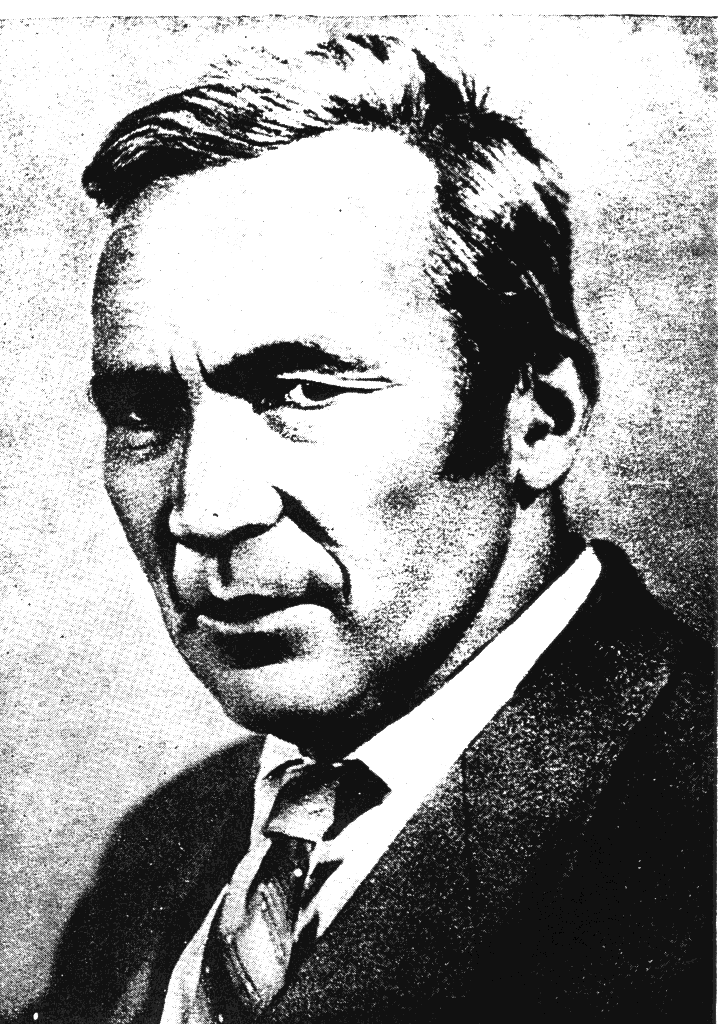История математических идей и открытий

Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В.Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

Самарской области

Тема «История математических идей и открытий»

Выполнила: Кашапова Ксения Эдуардовна

ученица 10 А класса

ГБОУ Клявлинская СОШ №2

им.В.Маскина ж.- д. ст. Клявлино

муниципального района Клявлинский

Самарской области

Учитель: Сербаева Ирина Алексеевна,

учитель математики

2017 г.

Оглавление

1. Введение……………………………………………………………….3-4

2. Основная часть

История математики…………………………………………………5-10

Галерея математических открытий и великих

ученых-математиков…………………………………………...........11-21

1. Вывод…………………………………………………………………..22

2. Литература……………………………………………………………..23

Введение.

Пристальное, глубокое изучение природы

есть источник самых плодотворных

открытий математики". (Ж. Фурье)

Иногда школьники говорят: «Мне математика не нужна, она мне не интересна, я буду учителем русского языка, или артисткой, или художником». Они, конечно, не правы. Кто с детских лет занимается математикой, тот развивает свой ум и внимание, воспитывает волю и настойчивость в достижении цели.

Так что же такое математика, какова её история идей и открытий? Какую роль играет развитие математики в жизни человека как науки?

Математика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии - матери наук - и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась. Начало Знаний у людей накапливалось все больше, в итоге произошло разделение точных и естественных наук.

Математика родилась в Греции. В странах-современниках Эллады математика использовалась либо для обыденных нужд (подсчёты, измерения), либо, наоборот, для магических ритуалов, имевших целью выяснить волю богов (астрология, нумерология и т. п.). Греки подошли к делу с другой стороны: они выдвинули тезис «Числа правят миром». Или, как сформулировали эту же мысль два тысячелетия спустя: «Природа разговаривает с нами на языке математики».

Греки проверили справедливость этого тезиса в тех областях, где смогли: астрономия, оптика, музыка, геометрия, позже — механика. Всюду были отмечены впечатляющие успехи: математическая модель обладала неоспоримой предсказательной силой. 

Актуальность

Развитие математики началось вместе с тем, как человек стал использовать абстракции  высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

После официального "рождения" математика пошла своим путем, развиваясь, укрепляя фундамент теорией, подкрепленной практикой. Казалось бы, какая практика может быть у математики, самой абстрактной из наук? Этот предмет способен описать абсолютно все процессы, происходящие на нашей планете и за ее пределами, а знание природы явления позволяет делать выводы и строить прогнозы. Отсюда можно сделать вывод, что все науки связаны между собой, наиболее очевидна эта зависимость между математикой и физикой. Поэтому в большинстве случаев великие математики и физики составляют одну группу ученых. Посудите сами - как можно описать что-то, не получив при этом обоснования? Математика – один из самых важных предметов и без математических знаний невозможно успешно изучать точные науки. Но в школьном курсе мало времени уделяется изучению истории математики и имен ученых- математиков, открытия и достижения которых перевернули все её восприятие и всемирное значение для жизни человека.

Проблема: Недостаточная информация о значительных открытиях и достижениях в математике в школьном курсе не дает учащимся полного представления о значимости математических знаний и умений в науке и в жизни.

Цель: Систематизировать материал по истории математики и показать значимость открытий и достижений великих ученых-математиков в науке.

Задачи:

1. Изучить историю математических открытий с древности до наших дней.

2. Изучить имена и вклад в развитие математики великих ученых.

3.Систематизировать изученный материал в галерею математических открытий.

Гипотеза:

Если я больше узнаю об истории математики и о вкладе учёных в развитие науки, и познакомлю с этой информацией одноклассников и учащихся школы, то у многих из них появится желание и интерес изучать математику как фундаментальную науку.

Основная часть

Кто хочет ограничиться настоящим,

без знания прошлого, тот никогда

его не поймет…

Лейбниц

Начальный период

Вплоть до VI века до н. э. греческая математика ничем выдающимся не прославилась. Были, как обычно, освоены счёт и измерение. Греческая нумерация (запись чисел), как позже римская, была аддитивной, то есть числовые значения цифр складывались. Первый её вариант (аттическая, или геродианова) содержали буквенные значки для 1, 5, 10, 50, 100 и 1000. Соответственно была устроена и счётная доска (абак) с камешками. Кстати, термин калькуляция (вычисление) происходит от calculus — камешек. Особый дырявый камешек обозначал нуль.

Позднее вместо аттической нумерации была принята алфавитная — первые 9 букв греческого алфавита обозначали цифры от 1 до 9, следующие 9 букв — десятки, остальные — сотни. Чтобы не спутать числа и буквы, над числами рисовали чёрточку. Числа, большие 1000, записывали позиционно, помечая дополнительные разряды специальным штрихом (внизу слева). Специальные пометки позволяли изображать и числа, большие 10000.

В VI веке до н. э. «греческое чудо» начинается: появляются сразу две научные школы — ионийцы (Фалес Милетский, Анаксимен, Анаксимандр) и пифагорейцы. О достижениях ранних греческих математиков мы знаем в основном по комментариям позднейших авторов, преимущественно Евклида, Платона и Аристотеля.

Ионийцы дали первые доказательства геометрических теорем. Однако главная роль в деле создания античной математики принадлежит пифагорейцам.

Школа Пифагорейцев. Милетская(Ионийская) школа.

Пифагорейская школа

Пифагор, основатель школы, как и Фалес, много путешествовал и тоже учился у египетских и вавилонских мудрецов. Вернувшись около 530 г. до н. э. в Великую Грецию (район южной Италии), он в городе Кротон основал нечто вроде тайного духовного ордена. Именно он выдвинул тезис «Числа правят миром», и с исключительной энергией занимался его обоснованием. В начале V в. до н. э., после неудачного политического выступления, пифагорейцы были изгнаны из Южной Италии, и союз прекратил свое существование, однако популярность учения от рассеяния только возросла. Пифагорейские школы появились в Афинах, на островах и в греческих колониях, а их математические знания, строго оберегаемые от посторонних, сделались общим достоянием.

Многие достижения, приписываемые Пифагору, вероятно, на самом деле являются заслугой его учеников. Пифагорейцы занимались астрономией, геометрией, арифметикой (теорией чисел), создали теорию музыки. Пифагор первый из европейцев понял значение аксиоматического метода, чётко выделяя базовые предположения (аксиомы, постулаты) и дедуктивно выводимые из них теоремы. Геометрия пифагорейцев в основном ограничивалась планиметрией (судя по дошедшим до нас позднейшим трудам, очень полно изложенной) и завершалась доказательством «теоремы Пифагора». Хотя изучались и правильные многогранники. Была построена математическая теория музыки. Зависимость музыкальной гармонии от отношений целых чисел (длин струн) была сильным аргументом пифагорейцев в пользу исконной математической гармонии мира, спустя 2000 лет воспетой Кеплером. Они были уверены, что «элементы чисел являются элементами всех вещей… и что весь мир в целом является гармонией и числом». В основе всех законов природы, полагали пифагорейцы, лежит арифметика, и с её помощью можно проникнуть во все тайны мира. В отличие от геометрии, арифметика у них строилась не на аксиоматической базе, свойства натуральных чисел считались самоочевидными, однако доказательства теорем и здесь проводили неуклонно.

Пифагорейцы немало продвинулись в теории делимости, но чрезмерно увлеклись играми с «треугольными», «квадратными», «совершенными» и т. п. числами, которым, судя по всему, придавали мистическое значение. Видимо, правила построения «пифагоровых троек» были открыты уже тогда; исчерпывающие формулы для них приводятся у Диофанта. Теория наибольших общих делителей и наименьших общих кратных тоже, видимо, пифагорейского происхождения. Вероятно, они же построили общую теорию дробей (понимаемых как отношения (пропорции), так как единица считалась неделимой), научились выполнять с дробями сравнение (приведением к общему знаменателю) и все 4 арифметические операции.

Первой трещиной в пифагорейской модели мира стало ими же полученное доказательство иррациональности, сформулированное геометрически как несоизмеримость диагонали квадрата с его стороной. Невозможность выразить длину отрезка числом ставила под сомнение главный тезис пифагорейства. Даже Аристотель, не разделявший их взгляды, выражал своё изумление по поводу того, что есть вещи, которые «нельзя измерить самою малою мерою».

Положение попытался спасти талантливый пифагореец Теэтет. Он (и позже Евдокс) предложили новое понимание числа, которое теперь формулировались на геометрическом языке, и проблем соизмеримости не возникало. Однако впоследствии выяснилось, что построение числовой алгебры на основе геометрии было стратегической ошибкой пифагорейцев; например, с точки зрения геометрии выражения x2 + x и даже x4 не имели геометрического истолкования, и поэтому не имели смысла. Позднее Декарт поступил наоборот, построив геометрию на основе алгебры, и добился громадного прогресса.

Аналитическая геометрия. Аналитическая (координатная) геометрия создавалась совершенно независимо математиком П. Ферма (1601-1655 гг.) и Р. Декартом. Это было сделано специально для расширения возможностей евклидовой геометрии в задачах на построение. Но Ферма оценивал свои работы только как переформулирование сочинения Аполлония. Истинное открытие — это осознание всего могущества алгебраических методов, которое принадлежит все же Декарту. Евклидова геометрическая алгебра требовала для каждого изобретения нового уникального метода, поэтому она не могла предложить количественную информацию, которая так необходима науке. Р. Декарт все же решил данную проблему путем формулировки геометрических задач алгебраически, то есть он решал сначала алгебраическое уравнение и только потом строил искомый результат — отрезок, который имел необходимую длину. Алгебраическая геометрия возникла именно тогда, когда Декарт приступил к рассмотрению неопределенных задач на построение путем решений, где является не одна, а сразу множество различных длин.
   Алгебраическая геометрия применяет алгебраические уравнения, чтобы представить исследование поверхностей и кривых. Декарт считал, что определенную приемлемую кривую можно записать при помощи единственного алгебраического уравнения относительно x и y. Данный подход стал важным шагом вперед, так как он включил не только число допустимых таких кривых, как циссоида и конхоида, но и значительно расширил область кривых. Таким образом, в XVII-XVIII в. в. большинство главных открытий, к примеру, циклоида или цепная линия, быстро смогли войти в обиход ученых.

    Скорее всего, самым первым математиком, который использовал уравнения для доказательств свойств конических сечений, стал Дж. Валлис (1616-1703 гг.). В 1865 году он алгебраическим методом получил все необходимые ему результаты, которые были представлены в книге «Начала» Евклида.
    Именно аналитическая геометрия смогла полностью поменять ролями геометрию и алгебру. Выдающийся французский математик Лагранж сказал: «Алгебра и геометрия, двигаясь своими путями, только замедляют свой прогресс, а приложения делают ограниченными. Однако, как только эти науки объединяются, они начинают заимствовать друг у друга новые жизненные силы и возможности, которые заставляют их обеих двигаться огромными шагами вперед к совершенству».

Средние века и возрождение

Средневековая Европа. Римская цивилизация не оставила заметного следа в математике, поскольку была слишком озабочена решением практических проблем. Цивилизация, сложившаяся в Европе раннего Средневековья (ок. 400-1100), не была продуктивной по прямо противоположной причине: интеллектуальная жизнь сосредоточилась почти исключительно на теологии и загробной жизни. Уровень математического знания не поднимался выше арифметики и простых разделов из Начал Евклида. Наиболее важным разделом математики в Средние века считалась астрология; астрологов называли математиками. А поскольку медицинская практика основывалась преимущественно на астрологических показаниях или противопоказаниях, медикам не оставалось ничего другого, как стать математиками.
Около 1100 в западноевропейской математике начался почти трехвековой период освоения сохраненного арабами и византийскими греками наследия Древнего мира и Востока. Поскольку арабы владели почти всеми трудами древних греков, Европа получила обширную математическую литературу. Перевод этих трудов на латынь способствовал подъему математических исследований. Все великие ученые того времени признавали, что черпали вдохновение в трудах греков.
Первым заслуживающим упоминания европейским математиком стал Леонардо Пизанский (Фибоначчи). В своем сочинении Книга абака (1202) он познакомил европейцев с индо-арабскими цифрами и методами вычислений, а также с арабской алгеброй. В течение следующих нескольких веков математическая активность в Европе ослабла. Свод математических знаний той эпохи, составленный Лукой Пачоли в 1494, не содержал каких-либо алгебраических новшеств, которых не было у Леонардо.
Возрождение. Среди лучших геометров эпохи Возрождения были художники, развившие идею перспективы, которая требовала геометрии со сходящимися параллельными прямыми. Художник Леон Баттиста Альберти (1404-1472) ввел понятия проекции и сечения. Прямолинейные лучи света от глаза наблюдателя к различным точкам изображаемой сцены образуют проекцию; сечение получается при прохождении плоскости через проекцию. Чтобы нарисованная картина выглядела реалистической, она должна была быть таким сечением. Понятия проекции и сечения порождали чисто математические вопросы. Например, какими общими геометрическими свойствами обладают сечение и исходная сцена, каковы свойства двух различных сечений одной и той же проекции, образованных двумя различными плоскостями, пересекающими проекцию под различными углами? Из таких вопросов и возникла проективная геометрия. Ее основатель - Ж.Дезарг (1593-1662) с помощью доказательств, основанных на проекции и сечении, унифицировал подход к различным типам конических сечений, которые великий греческий геометр Аполлоний рассматривал отдельно.

Начало современной математики

Наступление 17 в. в Западной Европе ознаменовалось важными достижениями в алгебре и арифметике. Были введены в обращение десятичные дроби и правила арифметических действий с ними. Настоящим триумфом стало изобретение в 1614 логарифмов Дж.Непером. К концу 17 в. окончательно сложилось понимание логарифмов как показателей степени с любым положительным числом, отличным от единицы, в качестве основания. С начала 16 в. более широко стали употребляться иррациональные числа. Б.Паскаль (1623–1662) и И.Барроу (1630–1677), учитель И.Ньютона в Кембриджском университете, утверждали, что такое число, как , можно трактовать лишь как геометрическую величину. Однако в те же годы Р.Декарт (1596–1650) и Дж.Валлис (1616–1703) считали, что иррациональные числа допустимы и сами по себе, без ссылок на геометрию.

Математики XVII века

В XVII веке быстрое развитие математики продолжается, и к концу века облик науки коренным образом меняется.

Рене Декарт в трактате «Геометрия» исправляет стратегическую ошибку античных математиков и восстанавливает алгебраическое понимание числа (вместо геометрического). Более того, он указывает способ перевода геометрических предложений на алгебраический язык (с помощью системы координат), после чего исследование становится намного эффективнее. Так родилась аналитическая геометрия. Декарт рассмотрел множество примеров, иллюстрирующих огромную мощь нового метода, и получил немало результатов, неизвестных древним. Особо следует отметить разработанную им математическую символику, близкую к современной. Аналитический метод Декарта немедленно взяли на вооружение Валлис, Ферма и многие другие видные математики. Пьер Ферма, Гюйгенс и Якоб Бернулли открывают новый раздел математики, которому суждено большое будущее —теорию вероятностей. Якоб Бернулли формулирует первую версию закона больших чисел. И, наконец, появляется не очень чёткая, но глубокая идея — анализ произвольных гладких кривых с помощью разложения их на бесконечно малые отрезки прямых. Первой реализацией этой идеи был во многом несовершенныйметод неделимых (Кеплер, Кавальери, Ферма), и уже с его помощью было сделано множество новых открытий. В конце XVII века идея неделимых была существенно расширена Ньютоном и Лейбницем, и появился исключительно могучий инструмент исследования — математический анализ. Это математическое направление стало основным в следующем, XVIII веке.Теория отрицательных чисел всё ещё находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»).Комплексные числа считались фиктивными, правила действий с ними не были окончательно отработаны. Более того, было неясно, все ли «мнимые числа» можно записать в виде a+bi или, скажем, при извлечении некоторого корня могут появиться мнимости, не сводящиеся к этой форме (так полагал даже Лейбниц). Только в XVIII веке Даламбер и Эйлерустановили, что комплексные числа замкнуты относительно всех операций, включая извлечение корня любой степени.

Во второй половине XVII века появляется научная периодика, ещё не специализированная по видам наук. Начало положили Лондон и Париж, но особо важную роль сыграл журнал Acta Eruditorum (1682, Лейпциг, на латинском языке).Французская Академия наук издаёт свои записки (Memoires) с 1699 года. Выходили эти журналы редко, и переписка продолжала оставаться незаменимым средством распространения информации.

Галерея математических открытий и великих

учёных-математиков.

Основные и значимые открытия:

1. Открытие нуля.

Это произошло в Индии , примерно в 5 веке до нашей эры. Это открытие было революционным, так как впервые математики начали работать с таким объектом, который не имел отношения к реальности. Ведь реальность само по себе не пустота, так сказать, по определению. Но существование нуля диктовалось самим развитием математики. В дальнейшем понятие нуля привело к появлению в математике отрицательных чисел и к теории алгебраических уравнений.

1. Открытие иррациональных чисел.

Это произошло в Древней Греции и сделал его Пифагор в 5-6 веках до нашей эры. Это открытие произошло, когда он доказал свою знаменитую теорему «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Открытие иррациональных чисел привело к возникновению понятия вещественного числа и понятию непрерывность. А уже понятие непрерывности привело к построению математических основ геометрии и математического анализа.

1. Открытие дифференциального и интегрального исчисления.

Это открытие произошло в конце 17в. в начале 18 в. Ньютоном и Лейбницем. Заслуга этих ученых в том, что они обобщили все методы в одну теорию, которая базируется на понятии бесконечно малой величины.

На дифференциальном и интегральном исчислении базируется вся современная инженерия, астрономия, физика и др. науки, а также вся современная техника. Именно поэтому это открытие ставят в один ряд с самыми высокими достижениями человеческой культуры, такими как изобретение денег, колеса, письменности, бухгалтерского учета и компьютера.

1. Доказательство полноты комплексных чисел.

Это открытие сделал сделал Карл Фридрих Гаусс в конце 18 века. Доказательство полноты комплексных чисел привело математиков к полному пересмотру своего отношения к этим числам. Из странного инструмента эти числа тут же превратились самые правильные числа. Именно поэтому вся современная математика базируется на комплексных числах.

1. Создание теории множеств.

Создателем теории множеств является Георг Кантор, работы которого относятся к концу 19 века. Это открытие стало значимым. С этого времени понятие бесконечности стало равноправным математическим объектом и появились строгие математические правила работы с бесконечностью. Математики так сильно переосмыслили свою науку, что весь современный язык математики базируется на теории множеств.

1. Открытие Фурье –разложения.

Это открытие сделал Жан Батист Фурье в начале 19 века. Он решил задачу о распространении тепла в твердом теле и при этом разлагал функции в тригонометрические ряды. На методах обобщенного Фурье-разложения базируется, например, вся квантовая механика стационарных состояний и другие разделы физики.

1. Создание теории групп.

Эта теория создавалась в течение 19 века многими математиками, такими, как Эйлер, Гаус, Галуа и др. Вся это теория связывает все разделы математики в единое целое. На теории групп базируется теория симметрии, теория преобразований, современная алгебра, дифференциальная геометрия и др. Это одна из продуктивных теорий математики.

Великие учёные-математики:

Архимед – древнегреческий математик, механик и инженер.

(287 до н. э. — 212 до н. э.)

Древнегреческий математик, физик, механик и инженер из Сиракуз..

Архимед был замечательным механиком практиком и теоретиком, но основным делом его жизни была математика. Его работы относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так же ходят легенды, что именно он открыл основной закон гидростатики и принцип рычага.

Пифагор Самосский –древнегреческий философ и математик

(570-490 гг. до н. э.)

Греческий математик Пифагор считается одним из самых великих. Он жил в Греции в 570-495 гг до н.э. Известен тем, что основал школу пифагорейцев. Также упоминается его имя в связи с известной теоремой в тригонометрии. Однако некоторые источники сомневаются, что именно он доказал ее.  Тем не менее, теорема Пифагора играет важную роль в современных измерениях и технологическом оборудовании. Можно даже назвать Пифагора отцом современной математики.

Евклид – древнегреческий математик

(ок. 300 г. до н. э.)

Считается отцом геометрии, а его великий труд «Элементы» - одной из самых великих работ по математике в истории. Евклид доказал множество теорем и гипотез.

Фалес – древнегреческий философ и математик из Милета

(640-548 до.н.э.)

«Отцом философии» Фалеса называли уже в древности. Фалес был знатного рода и получил на родине хорошее образование. Именем Фалеса названа геометрическая теорема.

Исаак Ньютон

(25.12.1642-20.03. 1727)

В 1707 году  вышла книга «Универсальная математика». В ней приведены разнообразные численные методы. Ньютон всегда уделял большое внимание приближённому решению уравнений. Знаменитый  метод Ньютона позволял находить корни уравнений с немыслимой ранее скоростью и точностью.

Рене Декарт

(31.03.1596 – 11.02.1650 г.)

Французский философ, физик и математик Рене Декарт известен своим методом радикального сомнения. Тем не менее, этот ученый внес большой вклад в математику. Вместе с Ньютоном и Лейбницем основал современное исчисление.

Готфрид Вильгельм Лейбниц

(21.07.1646 – 14.11.1716 г)

Саксонский философ, логик, математик, механик, физик, юрист, дипломат. Лейбниц независимо от Ньютона создал математический анализ-дифференциальное и интегральное исчисления, создал комбинаторику как науку, заложил основы математической логики, описал двоичную систему счисления, в механике сформулировал закон сохранения энергии.

Иоганн Карл Фридрих Гаусс

(30.04.1777 — 23.02.1855)

Выдающийся немецкий математик, астроном и физик. С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: алгебре, дифференциальной и неевклидовой геометрии, в математическом анализе, теории функций комплексного переменного, теории вероятностей, а также в астрономии, геодезии и механике.

Гаусс дал первое строгое доказательство основной теоремы алгебры. Он открыл кольцо целых комплексных гауссовых чисел, создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал геометрическую модель комплексных чисел и действий с ними.

Леонард Эйлер

(15.04.1707-7.09.1783 г.)

Он считается самым великим математиком в истории человечества. Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».

Пьер де Ферма

(17.08.1601-12.01.1665 г)

Наряду с Декартом, Ферма считается основателем аналитической геометрии. Ферма направил всю силу своего гения на математические исследования. И все же математика не стала его профессией. Ученые его времени не имели возможности посвятить себя целиком любимой науке. Ферма широко известен благодаря так называемой великой теореме Ферма.

Леонардо Пизанский

(около 1170-около 1250)

Один из самых великих математиков Средних Веков. Невозможно представить современный бухгалтерский и вообще финансовый учет без использования десятичной системы счисления и арабских цифр, начало использования которых в Европе было положено Леонардо.

Жозеф Луи Лагранж

(25.01.1736-10.04.1813)

Великий французский ученый восемнадцатого века ( математик, механик, астроном ) итальянского происхождения. Наибольшие свои достижения Жозеф Луи Лагранж продемонстрировал в области математических наук ( теория дифференциальных уравнений, теория чисел, алгебра и теория вероятностей, вариационное исчисление, решение задач на нахождение максимумов и минимумов ). Автор двух знаменитых математических трудов (Теория аналитических функций 1797 год. О решении численных уравнений 1798 год. ).

Георг Фридрих Бернхард Риман

(17.09.1826-20.07.1866 г)

Этот ученый стал одним из самых выдающихся математиков 19 в. У него большой вклад в геометрию, а многие теоремы носят его имя.  Гипотеза Римана входит в список семи «проблем тысячелетия», за решение каждой из которых Математический институт Клэя  выплатит приз в один миллион долларов США.

Софья Васильевна Ковалевская

(3.01.1850- 29.1891)

Принято считать, что женщинам лучше даются гуманитарные науки, а мужчинам точные. Это утверждение легко разбить, вспомнив великую женщину – математика – Софью Васильевну Ковалевскую. Первая в России и в Северной Европе женщина-профессор и первая в мире женщина — профессор математики. Главным же успехом Софьи Ковалевской в математики, ученые называют исследования, проведенные с задачей по вращению твердого тела вокруг неподвижной точки.

Михаил Васильевич Остроградский

(12.09.1801-20.12.1861)

Основные работы Остроградского относятся к прикладным аспектам математического анализа, механики, теории магнетизма, теории вероятностей. Михаил Васильевич Остроградский внес выдающийся вклад и в область математического анализа. Его результаты вошли в современную математику в качестве существенной и неотъемлемой ее части.

Алан Мэтисон Тьюринг

(23.061912-7.06.1954 г)

Английский математик, логик, криптограф. Один из самых великих умов 20 в. Во время второй мировой войны он сделал множество открытий и создал методы расшифровки закодированных сообщений немцев. Он также считается одним из первых настоящих ученых, работающих с компьютером.

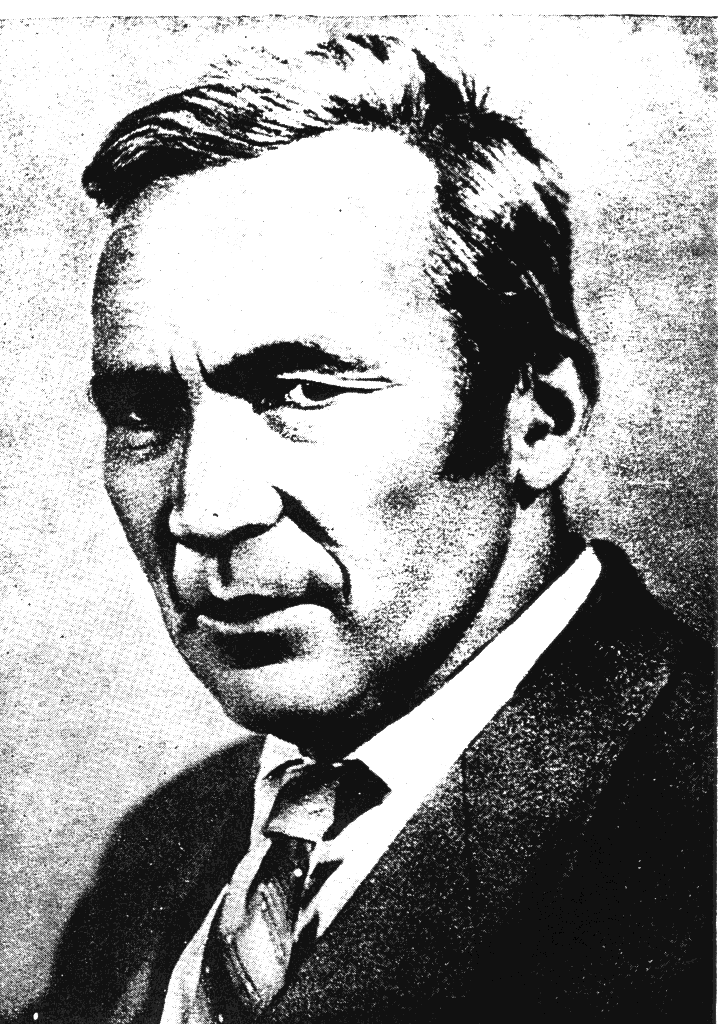
Андрей Николаевич Колмогоров

1. )

А.Н. Колмогоров — советский математик, один из основоположников современной теории вероятности, им получены основополагающие результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории тригонометрических рядов, теории функций, теории множеств и ряде других областей математики и её приложений.

Владимир Андреевич Стеклов

(09.01.1864—30.05.1926)

Русский и советский математик. Академик Петербургской АН (1912), вице-президент АН СССР (1919—26). Доктор физико-математических наук (1902), профессор (1896).

Труды по математической физике и теории дифференциальных уравнений. Основными направлениями исследований В.А. Стеклова в математической физике были задачи о распространении тепла, равновесии вращающейся массы, задачи электростатики и др. Занимался вопросами разложения функций в ряды по заданным ортогональным системам функций, которые непосредственно связаны с приложением метода Фурье к решению краевых задач.

В.А. Стеклову принадлежат важные исследования по теории дифференциальных уравнений, математическому анализу, теории упругости и гидромеханике. Основатель школы математической физики в нашей стране и один из блестящих представителей петербургской математической школы, созданной П. Л. Чебышевым. Под руководством Стеклова была налажена сеть сейсмологических станций, издание книг и научных журналов по математике. Организовал физико-математический институт при АН СССР, который впоследствии разделился на три научных учреждения. Среди них — Математический институт имени В. А. Стеклова. Именем Стеклова названо серое пятно на обратной стороне Луны.

Вывод:

Данная работа показывает, что история математики складывается из великих достижений великих людей. Математика развивалась постепенно, но великие открытия ученых преобразили науку. Каждый из этих людей внес свой особенный вклад, который помог дальнейшему развитию нашего мира и других наук. Благодаря им, современная математика является всеобщей научной дисциплиной, она близка к реально происходящим жизненным процессам. Математика и математический стиль мышления совершают триумфальный марш как в науке, так и в её применениях. Учащиеся должны почувствовать это и относиться к математике с большим интересом, увлечением и пониманием необходимости математических знаний, как для будущей их деятельности, так и для жизни и развития всего общества.

• «Числа управляют миром», – говорили пифагорейцы. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники наших дней. (А. Дородницын)

• Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. (А.Н. Крылов)

• Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин)

• Разве ты не заметил, что способный к математике изощрен во всех науках в природе? (Платон)

Литература и интернет ресурсы:

1. Г.И. Глейзер История математики в школе IV-VI классы М. «Просвещение» 1981 г.

2. Г.И. Глейзер История математики в школе VII-VIII классы М. «Просвещение» 1982 г.

3. https://ru.wikipedia.org/wiki/История_математики

4. https://interneturok.ru/velikie-otkrytiya-v-matematike

5. http://fb.ru/article/170806/velikie-matematiki-i-ih-otkryitiya

6. http://quarkon.ru/math/history.htm

21