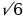Итоговая контрольная работа по алгебре за курс 10 класса (базовый уровень) 2023/2024 учебный год
Контрольная работа по алгебре и началам анализа, по учебнику «Алгебра и начала математического анализа 10-11 классы» авторы: Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачёва и др., Просвещение ,2014
Цель работы – оценить уровень овладения обучающимися знаний материала по алгебре учащихся 10-го класса и определить характер сформированной необходимых учебных компетенций.
Пояснительная записка
Данная контрольная работа рассчитана на 2 урока.
Работа содержит 9 заданий: Баллы, полученные за выполненные задания, суммируются.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Итого |
| Баллы | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 3 | 2 | 15 |
Схема перевода баллов в школьную оценку
Максимальное количество баллов по алгебре - 15 баллов
| Балл | 0-6 | 7-10 | 11-13 | 14-15 |
| Оценка | 2 | 3 | 4 | 5 |
1. Содержание контрольно-измерительных материалов отражает следующие разделы:
Функция, способы задания функции. График функции. Взаимно обратные функции.
Иррациональные уравнения и неравенства;
Целые и дробно-рациональные уравнения и неравенства.
Арифметический корень натуральной степени. Действия с арифметическими корнями натуральной степени
преобразование тригонометрических выражений, Основные тригонометрические формулы.
Тригонометрические уравнения;
Бесконечно убывающая геометрическая прогрессия. Сумма бесконечно убывающей геометрической прогрессии
2. Требования, предъявляемые к знаниям и умениям учащихся:
выполнять арифметические действия, сочетая устные и письменные приемы, находить значения корня натуральной степени, степени с рациональным показателем
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, и тригонометрические функции;
выполнять преобразования тригонометрических выражений решать тригонометрические уравнения;
выполнять преобразования целых, рациональных и иррациональных выражений и решать основные типы целых, рациональных и иррациональных уравнений и неравенств.
Содержание заданий контрольной работы
| Номер заданий из к/р. | Темы |
| 1 | Решение рационального и иррационального уравнения |
| 2 | Решение рационального и иррационального неравенства |
| 3 | Преобразование выражений содержащих корень натуральной степени |
| 4 | Вычисление выражений содержащих корень |
| 5 | Нахождение функции обратной данной, области определения и множества значений функции |
| 6 | Преобразование тригонометрических выражений |
| 7 | Преобразование тригонометрических выражений при заданном значении аргумента |
| 8 | Решение простейших тригонометрических уравнений |
| 9 | Нахождение неизвестного члена бесконечно убывающей геометрической прогрессии |
1 вариант
1.Решите уравнения: а)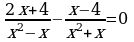 . б)
. б)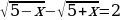
2. Решите неравенства : а)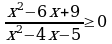 б)
б)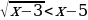
3.Упростите выражение: 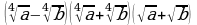 .
.
4. Вычислите:
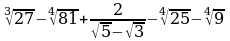
5.Найти функцию, обратную к данной, ее область определения и множество значений:
а) у =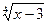 ; б) у = 3х – 5.
; б) у = 3х – 5.
6.Упростите выражение:
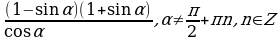 ;
;
7. Упростите выражение:
sin(α-β) - 2cosαsinβ, если α + β = π;
8. Решите уравнения
а) sin x = 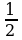 ; б)
; б) 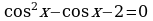 в)
в) 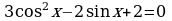
9 Найдите первый член бесконечно убывающей геометрической прогрессии, если
а)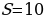 q =
q = 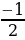 б)
б) 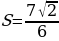 q =
q = 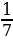
2 вариант
1.Решите уравнения а)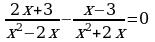 а)
а)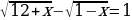
2.Решите неравенства а)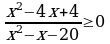 б)
б)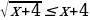
3.Упростите выражение: 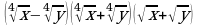 .
.
4.Вычислите:
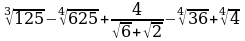
5.Найти функцию, обратную к данной, ее область определения и множество значений:
а) у =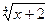 ; б) у = 2х +4.
; б) у = 2х +4.
6.Упростите выражение:
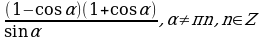
7.Упростите выражение:
sin(α+β) + 2sinβcosα, если α – β =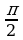
8.Решите уравнения
а) cos x = 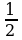 ; б)
; б) 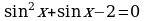 в)
в) 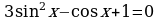
9.Найдите первый член бесконечно убывающей геометрической прогрессии, если
а)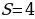 q =
q = 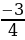 б)
б) 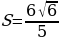 q =
q = 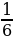
ответы
| № задания | 1 вариант | 2 вариант |
| 1 | а)х=-11 б)х=-4 | а)х=-12 б)х=-3 |
| 2 | а)х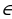 (-∞,-1) (-∞,-1)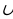 (5;+∞) (5;+∞) б)х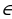 (7;+∞) (7;+∞) | а)х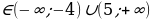 б)х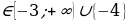 |
| 3 | a-b | х-у |
| 4 | 0 | 0 |
| 5 | а)y=3+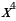 б)y=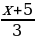 | а)у=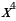 -2 -2 б)у=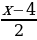 |
| 6 | 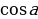
| 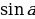
|
| 7 | - | - |
| 8 | а)х=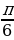 +2k +2k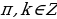 х=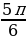 +2k +2k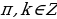 б)х=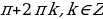 в)х=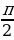 +2 +2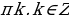 | а) х=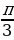 +2 +2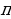 k,k k,k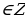 )х=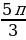 +2 +2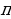 k,k k,k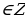 б) х=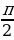 +2 +2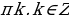 в)х=2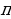 k,k k,k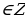 |
| 9 | 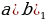 =15 =15 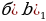 = =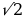
| а)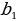 =7 =7 б)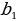 = =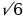 |
Составитель: учитель математики 1 категории Юрковец Н.Н.






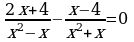 . б)
. б)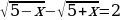
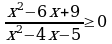 б)
б)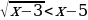
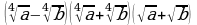 .
.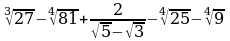
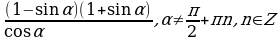 ;
;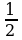 ; б)
; б) 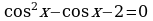 в)
в) 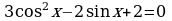
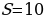 q =
q = 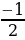 б)
б) 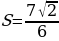 q =
q = 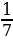
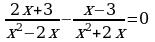 а)
а)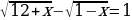
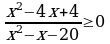 б)
б)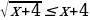
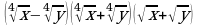 .
.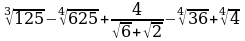
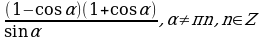
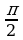
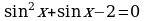 в)
в) 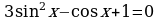
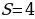 q =
q = 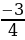 б)
б) 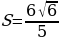 q =
q = 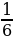
 (-∞,-1)
(-∞,-1) (5;+∞)
(5;+∞)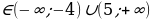
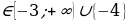
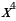
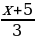
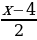
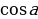
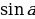
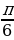 +2k
+2k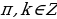
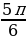 +2k
+2k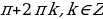
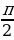 +2
+2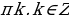
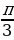 +2
+2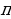 k,k
k,k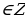
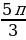 +2
+2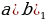 =15
=15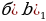 =
=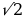
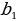 =7
=7