Итоговая контрольная работа по геометрии в 9 классе.

Ф.И., класс __________________________________________________ Дата __________________

Геометрия. Вариант 1.

1. 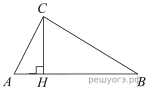 В прямоугольном треугольнике ABC катет AC = 50, а высота CH, опущенная на гипотенузу, равна  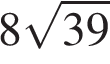. Найдите  .

Ответ: _____________________________________________________________________________

2. 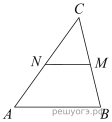 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 97. Найдите площадь четырёхугольника ABMN.

Ответ: _____________________________________________________________________________

3. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.

Ответ: _____________________________________________________________________________

4.

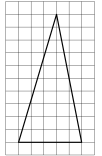
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник. Найдите его площадь.

Ответ: _____________________________________________________________________________

5.

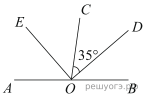
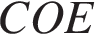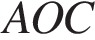Найдите величину угла   , если     — биссектриса угла   ,    — биссектриса угла   .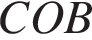

6*. В остроугольном треугольнике ABC проведены высоты AA₁ и BB₁. Докажите, что углы BB₁A₁ и BAA₁ равны.

Ф.И., класс __________________________________________________ Дата __________________

Геометрия. Вариант 2.

1.

Тангенс острого угла прямоугольной трапеции равен  . Найдите её большее основание, если меньшее основание равно высоте и равно 40.

Ответ: _____________________________________________________________________________

2.

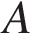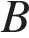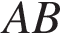На окружности с центром в точке   отмечены точки   и   так, что  . Длина меньшей дуги   равна 61. Найдите длину большей дуги  .

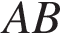Ответ: _____________________________________________________________________________

3.

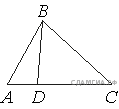
На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC = 7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.

Ответ: _____________________________________________________________________________

4.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

Ответ: _____________________________________________________________________________

5. Биссектриса угла A параллелограмма   пересекает его сторону 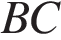  в точке  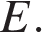 Найдите площадь параллелограмма   если     а 

6.* В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OL равны.