В а р и а н т 1
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 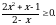
Решите неравенство 35х – 7 ≥ 27х.
Решите уравнение 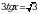 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Установить, на каком рисунке изображён эскиз графика функции y = 2x.
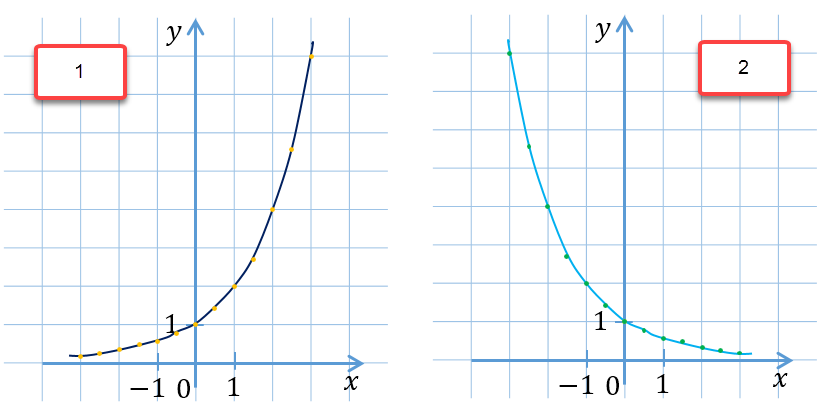
Найдите значение выражения 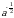 :
: 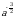 при а = 2.
при а = 2.
Вычислите 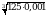
Найдите значение выражения 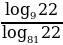 .
.
Вычислите tgα, если 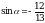 и π α .
и π α .
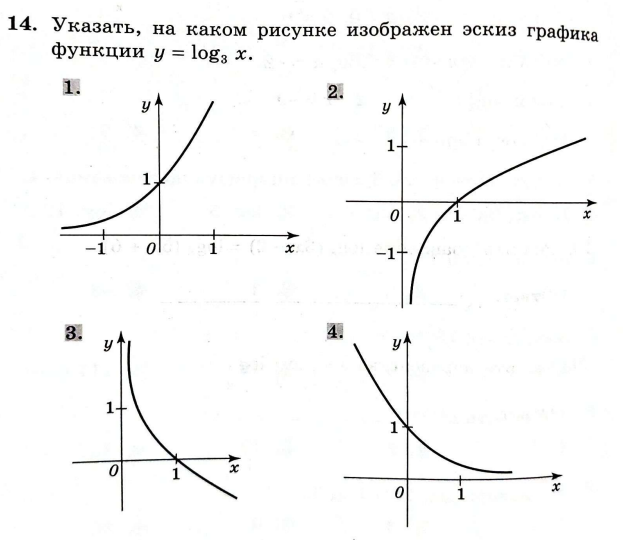
Решите уравнение log3 4х = 2.
Решите уравнение 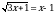 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 24, BD = 20. Найдите боковое ребро SC.
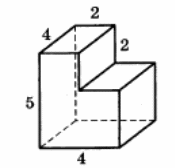
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 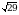 , BB1 = 2, B1C1 = 3. Найдите длину ребра АВ.
, BB1 = 2, B1C1 = 3. Найдите длину ребра АВ.
У Пети есть 30 тетрадей, из них 18 тетрадей в линейку, остальные — в клетку. Найдите вероятность того, что случайно выбранная Петина тетрадь окажется тетрадью в клетку.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство
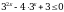 .
.
Решите уравнение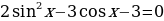 .
.
В а р и а н т 2
ЧАСТЬ 1
|
| Запишите решение заданий 1 – 14. |
|
Решите неравенство 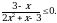
Решите неравенство log0,25(x – 1) – 2.
Решите уравнение tg5x = – 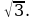
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
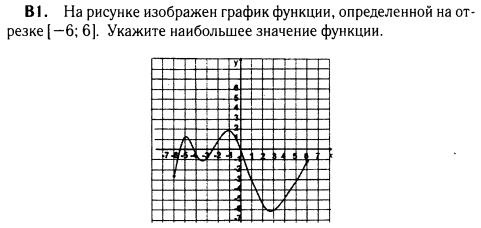
На рисунке изображён график функции, определённой на отрезке 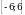 . Укажите наибольшее значение функции.
. Укажите наибольшее значение функции.
Найдите значение выражения 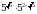 .
.
Вычислите 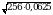 .
.
Найдите значение выражения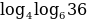 .
.
Найдите 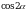 , если
, если 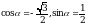 .
.
Найдите корень уравнения 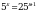 .
.
Решите уравнение 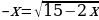 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SС = 13, BD = 24. Найдите длину отрезка SО.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
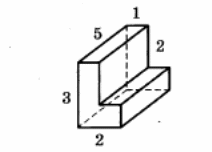
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны D1С1 = 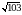 , АА1 = 3, А1D1 = 3. Найдите длину диагонали С1А.
, АА1 = 3, А1D1 = 3. Найдите длину диагонали С1А.
Вероятность того, что новый принтер прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,86. Найдите вероятность того, что он прослужит больше года, но не больше двух лет.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 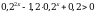 .
.
Решите уравнение 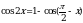 .
.
В а р и а н т 3
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 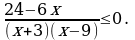
Решите неравенство 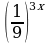
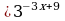 .
.
Решите уравнение 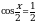 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите график функции, заданной формулой 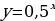 .
.
Найдите значение выражения 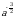 :
: 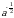 при а = 2.
при а = 2.
Вычислите 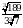 .
.
Найдите значение выражения 5 – log 3(34).
Вычислите значение sinα, если cosα = 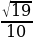 и
и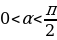 .
.
Решите уравнение log7(1 - 3х) = 2.
Решите уравнение 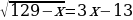 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 24, SA = 26. Найдите длину отрезка AC.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
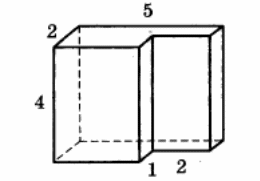
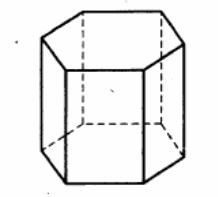
Найдите площадь боковой поверхности правильной шестиугольной призмы, стороны основания которой равны 3, а высота – 6.
В коробке 50 глазированных сырков, из них 17 с изюмом. Вася достаёт из коробки один сырок. Найдите вероятность того, что ему попадётся сырок без изюма.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство  .
.
Решите уравнение 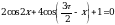 .
.
В а р и а н т 4
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 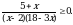
Решите неравенство log0,5(4 – 0,4x) – 1.
Решите уравнение 2sin5x – 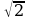 = 0.
= 0.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
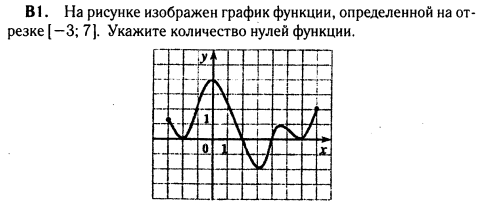
На рисунке изображён график функции, определённой на отрезке 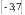 . Укажите количество нулей функции.
. Укажите количество нулей функции.
Найдите значение выражения 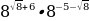 .
.
Вычислите 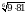
Вычислите log12160 + log120,9.
Найдите значение 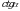 , если
, если 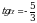 .
.
Решите уравнение 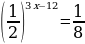 .
.
Решите уравнение 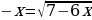 .
.
В правильной треугольной пирамиде SABC точка М – середина ребра АВ, S – вершина. Известно, что ВС = 4, SМ = 3. Найдите площадь боковой поверхности.
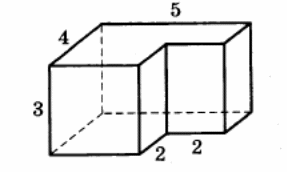
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Вероятность того, что новый чайник прослужит больше года, равна 0,95. Вероятность того, что он прослужит больше двух лет, равна 0,83. Найдите вероятность того, что он прослужит больше года, но не больше двух лет.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 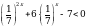 .
.
Решите уравнение 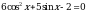 .
.
В а р и а н т 5
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 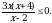
Решите неравенство 53 – 2х ≤ 125х.
Решите уравнение 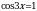 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите, на каком рисунке изображён эскиз графика функции 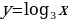 .
.
Вычислите 7 + 17 ·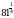 .
.
Вычислите 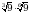 .
.
Найдите значение выражения 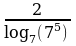 .
.
Вычислите 4sin15° 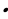 cos15°.
cos15°.
Решите уравнение 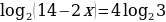 .
.
Решите уравнение 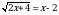 .
.
В правильной треугольной пирамиде SABC точка К – середина ребра ВС, S – вершина. Известно, что АВ = 6, а площадь боковой поверхности равна 63. Найдите длину отрезка SК.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
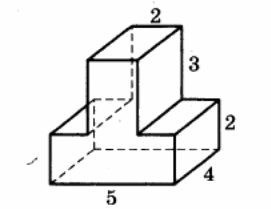
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
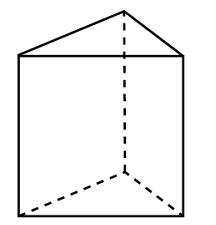
В столовой на подносе вперемешку лежат 60 пирожков — 24 с капустой, остальные с вишней. Внешне все пирожки одинаковы. Найдите вероятность того, что случайно выбранный пирожок окажется с вишней.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 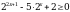 (базовый уровень).
(базовый уровень).
Решите уравнение 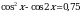 .
.
В а р и а н т 6
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 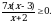
Решите неравенство log2 x 3.
Решите уравнение cos3х =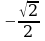 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите график функции, ограниченной снизу.
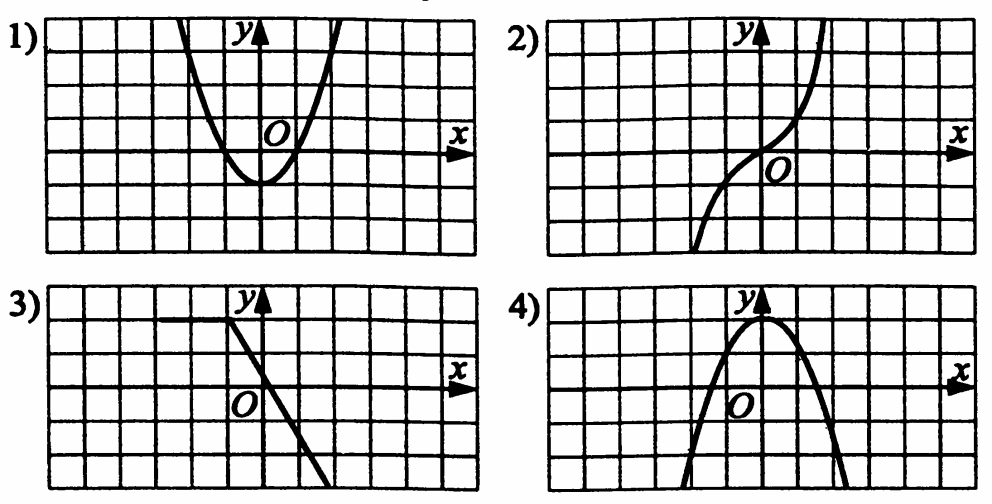
Найдите значение выражения 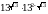 .
.
Вычислите 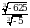 .
.
Найдите значение выражения log 390 + log30,3.
Найдите 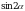 , если
, если 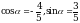 .
.
Решите уравнение 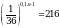 .
.
Найдите сумму корней уравнения 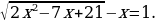
В правильной треугольной пирамиде SABC точка R – середина ребра ВС, S – вершина. Известно, что SR = 16, а площадь боковой поверхности равна 168. Найдите длину отрезка AB.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
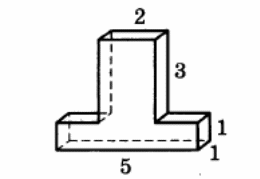
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
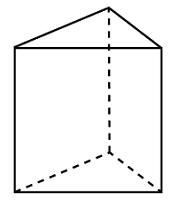
Из районного центра в село ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 30 пассажиров, равна 0,91. Вероятность того, что пассажиров окажется меньше 20, равна 0,65. Найдите вероятность того, что в понедельник число пассажиров окажется от 20 до 29.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 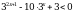 .
.
Решите уравнение 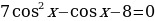 .
.
В а р и а н т 7
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 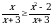 .
.
Решите неравенство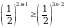 .
.
Решите уравнение 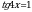 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите номер рисунка, на котором изображён график функции y = 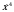 .
.
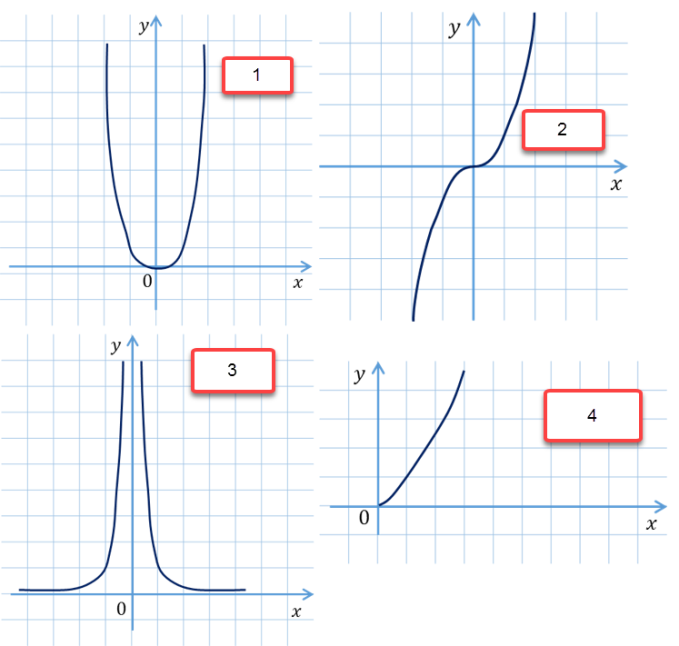
Вычислите 23 – 5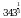 .
.
Вычислите 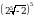 .
.
Найдите значение выражения 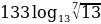 .
.
Упростите выражение sin40°·cos28° - sin28°· cos40° - sin12°.
Решите уравнение 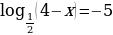 .
.
Решите уравнение 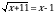 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 7, АС = 48. Найдите боковое ребро SВ.
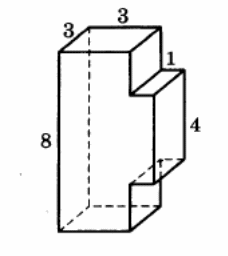
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 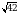 , BB1 = 4, B1C1 = 1. Найдите длину ребра А1В1.
, BB1 = 4, B1C1 = 1. Найдите длину ребра А1В1.
В сборнике билетов по химии всего 28 билетов, в 7 из них встречается вопрос о кислотах. Найдите вероятность того, что в случайно выбранном на экзамене билете не окажется вопроса о кислотах.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 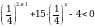 .
.
Решите уравнение 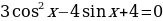 .
.
В а р и а н т 8
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 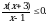
Решите неравенство 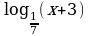 –1.
–1.
Решите уравнение cos 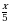 =
= 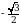 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Установить, на каком рисунке изображён эскиз графика функции 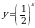 .
.
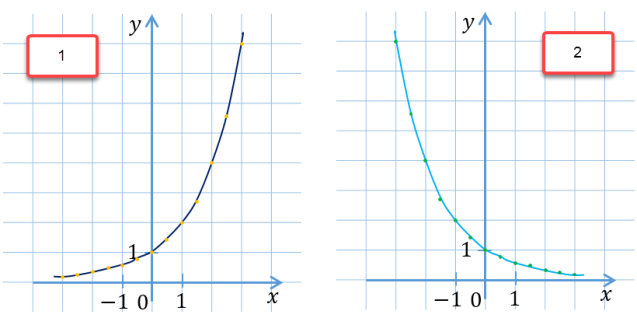
Найдите значение выражения 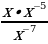 при х = 6.
при х = 6.
Вычислите 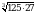 .
.
Найдите значение выражения – 4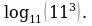
Найдите 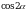 , если
, если 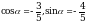 .
.
Решите уравнение 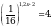
Решите уравнение 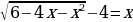 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SС = 15, АС = 18. Найдите длину отрезка SО.
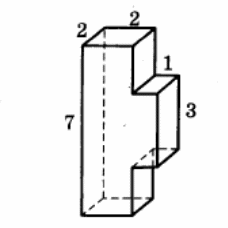
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны D1С1 = 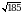 , АА1 = 2, А1D1 = 6. Найдите длину диагонали С1А.
, АА1 = 2, А1D1 = 6. Найдите длину диагонали С1А.
Из областного центра в маленький город ходит ежедневная электричка. Вероятность того, что в среду в электричке окажется меньше 80 пассажиров, равна 0,93. Вероятность того, что пассажиров окажется меньше 50, равна 0,57. Найдите вероятность того, что в среду число пассажиров окажется от 50 до 79.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 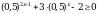 .
.
Решите уравнение 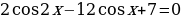 .
.
В а р и а н т 9
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 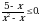
Решите неравенство 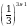
Решите уравнение 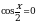 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
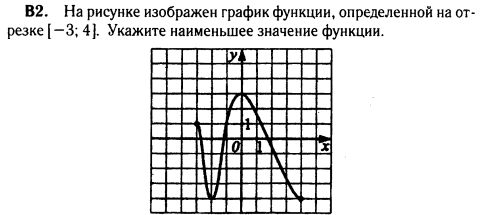
На рисунке изображён график функции, определённой на отрезке 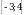 . Укажите наименьшее значение функции.
. Укажите наименьшее значение функции.
Найдите значение выражения 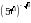 .
.
Вычислите 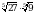 .
.
Найдите значение выражения 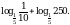
Найдите значение 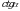 , если
, если 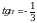 .
.
Найдите произведение корней уравнения log11(х2 + 21) =2.
Найдите среднее арифметическое корней уравнения 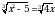 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 7, SD = 25. Найдите длину отрезка BD.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
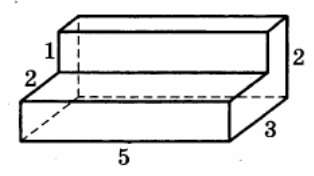
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
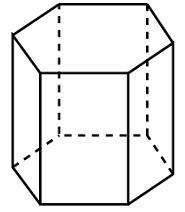
В сборнике билетов по истории всего 24 билета, в 15 из них встречается вопрос по курсу истории древнего Рима. Найдите вероятность того, что в случайно выбранном на экзамене билете не окажется вопроса по истории древнего Рима.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 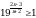 (базовый уровень).
(базовый уровень).
Решите уравнение 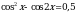 .
.
В а р и а н т 10
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 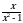
Решите неравенство 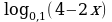 ≥ –1.
≥ –1.
Решите уравнение cos2х = 1.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите количество нулей функции на рисунке.
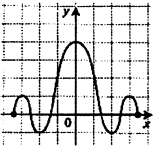
Вычислите 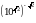 .
.
Вычислите 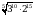 .
.
Найдите значение выражения log 550 + log5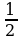 .
.
Найдите 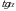 , если
, если 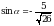 и
и 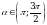 .
.
Решите уравнение 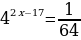 .
.
Найдите сумму корней уравнения 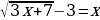 .
.
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что АВ = 6, SМ = 5. Найдите площадь боковой поверхности.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
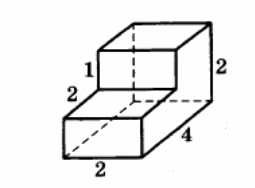
Найдите боковое ребро правильной четырехугольной призмы, если стороны ее основания равны 3, а площадь поверхности равна 66.
По данным многолетних наблюдений установлено, что вероятность того, что в городе М годовое количество осадков превысит 2200 мм, равна 0,43. Вероятность того, что осадков за год окажется меньше 1600 мм, равна 0,28. Найдите вероятность того, что количество осадков в городе М в следующем году окажется в промежутке от 1600 до 2200 мм.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 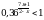 .
.
Решите уравнение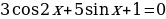 .
.
В а р и а н т 11
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 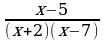 0.
0.
Решите неравенство (0,7)7 – 3х 2х – 3 .
Решите уравнение 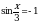 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите номер рисунка, на котором изображён график функции y = х4.

Найдите значение выражения 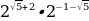 .
.
Вычислите 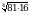 .
.
Найдите значение выражения 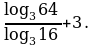
Упростите выражение 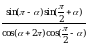 .
.
Решите уравнение 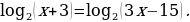
Решите уравнение 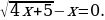
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что АВ = 6, а площадь боковой поверхности равна 45. Найдите длину отрезка SМ.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
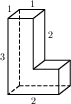
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.

В чемпионате по прыжкам с шестом участвуют 72 спортсменки: 28 из России, 17 из Казахстана, остальные — из Белоруссии. Порядок, в котором выступают спортсменки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 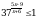 .
.
Решите уравнение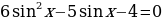 .
.
В а р и а н т 12
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 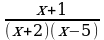 0.
0.
Решите неравенство 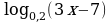 ≥ –1.
≥ –1.
Решите уравнение sinх – 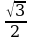 = 0.
= 0.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
На рисунке схематически изображён график функции
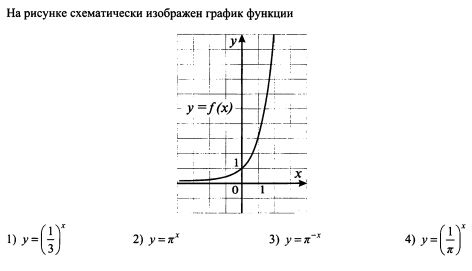
Вычислите 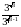 .
.
Вычислите 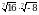 .
.
Найдите значение выражения 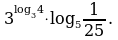
Найдите 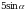 , если
, если 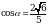 и
и 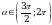 .
.
Решите уравнение 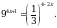
Решите уравнение 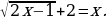
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что SМ = 5, а площадь боковой поверхности равна 45. Найдите длину отрезка AB.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
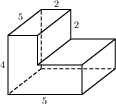
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.
Гигрометр измеряет влажность в зернохранилище. Вероятность того, что влажность окажется выше 35 %, равна 0,86. Вероятность того, что влажность окажется ниже 58 %, равна 0,71. Найдите вероятность того, что влажность находится в пределах от 35 % до 58 %.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 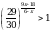 .
.
Решите уравнение 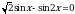 .
.
В а р и а н т 13
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 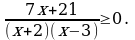
Решите неравенство (1,1)6 + 5х (1,1)27 - 2х.
Решите уравнение 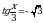 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
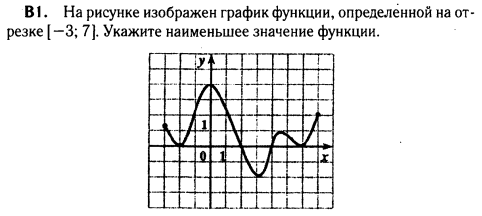
На рисунке изображён график функции, определённой на отрезке 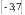 . Укажите наименьшее значение функции.
. Укажите наименьшее значение функции.
Вычислите 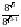 .
.
Вычислите 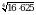 .
.
Найдите значение выражения 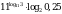 .
.
Упростите выражение (1 + tg2α)cos2α.
Решите уравнение log3(5х 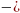 6) = 2.
6) = 2.
Решите уравнение 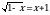 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 24, АС = 14. Найдите боковое ребро SD.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
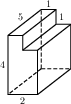
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что АС1 = 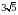 , BB1 = 2, А1D1 = 5. Найдите длину ребра DC.
, BB1 = 2, А1D1 = 5. Найдите длину ребра DC.
На олимпиаде по астрономии 200 участников разместили в трёх аудиториях. В первых двух удалось разместить по 55 человек, оставшихся участников перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 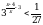 .
.
Решите уравнение 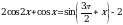 .
.
В а р и а н т 14
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 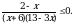
Решите неравенство 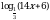 ≥
≥ 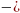 3.
3.
Решите уравнение tg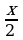 = –1.
= –1.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите количество нулей функции на рисунке.
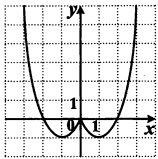
Найдите значение выражения 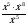 при х = 7.
при х = 7.
Вычислите 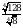 .
.
Вычислите 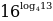 .
.
Найдите 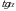 , если
, если 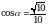 и
и 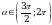 .
.
Решите уравнение 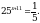
Найдите сумму корней уравнения 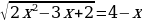 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SD = 15, АС = 24. Найдите длину отрезка SО.
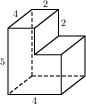
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны DС = 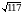 , АА1 = 6, А1D1 = 4. Найдите длину диагонали АС1.
, АА1 = 6, А1D1 = 4. Найдите длину диагонали АС1.
Вероятность того, что в городе К. солнечных дней в году будет 300 или больше, равна 0,36. Найдите вероятность того, что в следующем году в этом городе солнечных дней будет меньше, чем 300.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 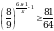 .
.
Решите уравнение 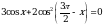 .
.
В а р и а н т 15
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 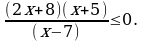
Решите неравенство 2 7х -1 ≥ 43х + 5.
Решите уравнение 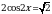 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите номер рисунка, на котором изображён график функции y = 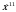 .
.

Выполните действия 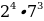 ׃
׃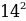 .
.
Вычислите 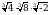 .
.
Найдите значение выражения 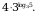
Найдите значение 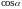 , если
, если 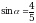 , 0 .
, 0 .
Решите уравнение log2(7 + х) = 3.
Решите уравнение 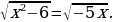
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 24, SС = 25. Найдите длину отрезка BD.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
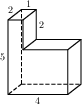
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 5.

В спортивный праздник проходили соревнования внутри школы. Из 80 школьников 32 играли в футбольном турнире, другие 24 — в баскетбольном, а остальные болели за свои команды. Найдите вероятность того, что случайно выбранный школьник был болельщиком.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 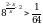 .
.
Решите уравнение 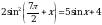 .
.
В а р и а н т 16
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 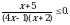
Решите неравенство 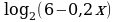 ≥ 2.
≥ 2.
Решите уравнение 2cosx = –1.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
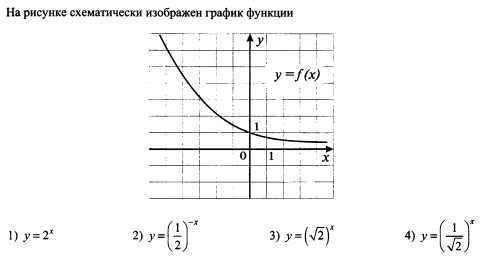
На рисунке схематически изображён график функции
Найдите значение выражения 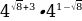 .
.
Вычислите 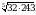 .
.
Найдите значение выражения log3900 – 2log310.
Найдите 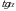 , если
, если 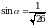 и
и 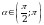 .
.
Решите уравнение 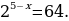
Найдите сумму корней уравнения 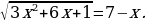
В правильной треугольной пирамиде SABC точка N – середина ребра ВС, S – вершина. Известно, что АВ = 6, SN = 6. Найдите площадь боковой поверхности.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
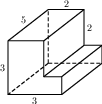
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 8, а площадь поверхности равна 416.

Вероятность того, что в случайный момент времени атмосферное давление в некотором городе ниже 745 мм рт. ст., равна 0,53. Найдите вероятность того, что в случайный момент времени давление равно 745 мм рт. ст. или выше этого значения.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 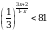 .
.
Решите уравнение 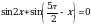 .
.
В а р и а н т 17
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 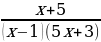
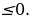
Решите неравенство 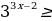
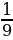 .
.
Решите уравнение 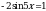 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
На каком рисунке схематически изображён график функции 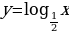 .
.
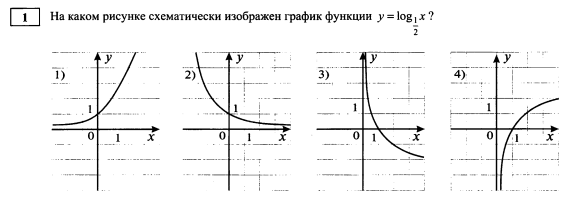
Найдите значение выражения 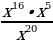 при х = 2.
при х = 2.
Вычислите 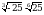 .
.
Найдите значение выражения 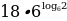 .
.
Найдите 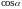 , если
, если 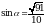 и
и 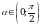 .
.
Решите уравнение 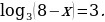
Решите уравнение 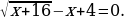
В правильной треугольной пирамиде SABC точка N – середина ребра ВС, S – вершина. Известно, что АВ = 6, а площадь боковой поверхности равна 54. Найдите длину отрезка SN.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
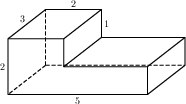
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

На день рождения Вася устроил беспроигрышную лотерею для своих одноклассников. Всего было 30 призов: 11 шоколадок, 10 пакетиков сока, остальные призы — конфеты. Каждому (включая Васю) достаётся один случайный приз. Найдите вероятность того, что Васе достанется конфета.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 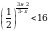 (базовый уровень).
(базовый уровень).
Решите уравнение 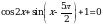 .
.
В а р и а н т 18
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 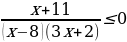 .
.
Решите неравенство 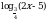
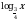 .
.
Решите уравнение 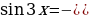
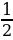 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
Укажите количество нулей функции на рисунке.
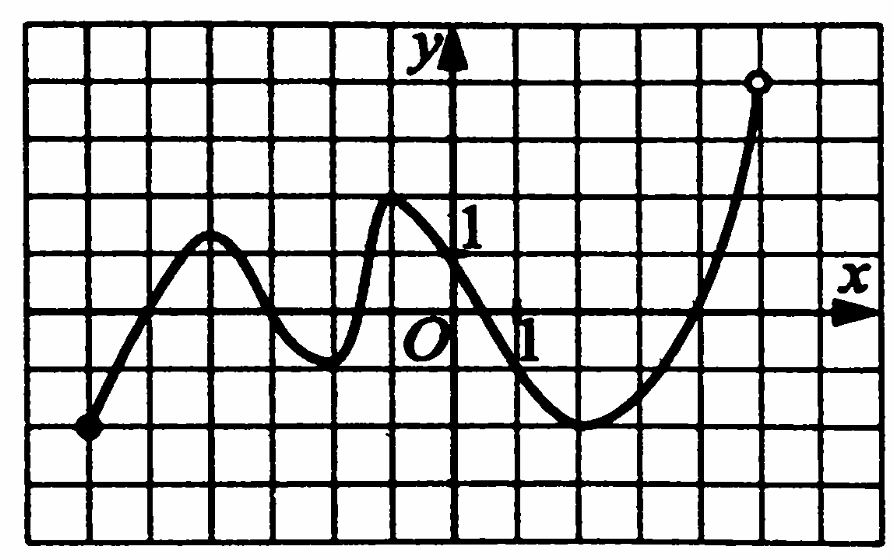
Найдите значение выражения 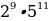 ׃
׃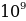 .
.
Вычислите 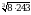 .
.
Вычислите 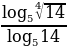 .
.
Найдите 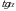 , если
, если 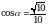 и
и 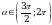 .
.
Решите уравнение 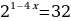 .
.
Решите уравнение 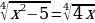 .
.
В правильной треугольной пирамиде SABC точка N – середина ребра ВС, S – вершина. Известно, что SN = 6, а площадь боковой поверхности равна 54. Найдите длину отрезка AB.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
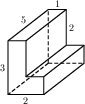
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

На столе лежит 32 экзаменационных билета по теории вероятностей. Студент выучил ответы на все вопросы, кроме вопросов по теме «Комбинаторика». Известно, что вопросы по этой теме встречаются в 12 билетах. Студент случайным образом выбирает один билет. Какова вероятность того, что в этом билете нет вопросов по теме «Комбинаторика»?
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 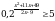 .
.
Решите уравнение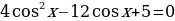 .
.
В а р и а н т 19
ЧАСТЬ 1
|
| Запишите решение заданий 1 – 14. |
|
Решите неравенство 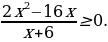
Решите неравенство 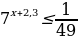 .
.
Решите уравнение 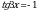 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
На каком рисунке схематически изображён график функции y = x4 – 1.
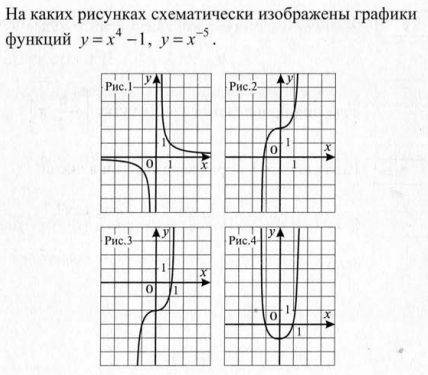
Найдите значение выражения 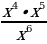 при х = 7.
при х = 7.
Вычислите 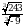 .
.
Найдите значение выражения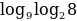 .
.
Найдите 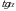 , если
, если 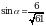 и
и 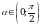 .
.
Найдите корень уравнения 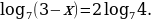
Решите уравнение 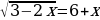 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 15, АС = 40. Найдите боковое ребро SD.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
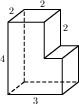
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что АС1 = 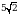 , BB1 = 5, А1D1 = 4. Найдите длину ребра DC.
, BB1 = 5, А1D1 = 4. Найдите длину ребра DC.
Научная конференция проводится 4 дня. Всего запланировано 60 докладов — первые два дня по 18 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора П. Порядок докладов определяется жребием. Какова вероятность того, что доклад профессора П. окажется запланирован на последний день конференции?
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство
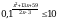 .
.
Решите уравнение 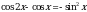 .
.
В а р и а н т 20
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 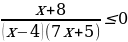 .
.
Решите неравенство 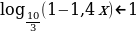 .
.
Решите уравнение 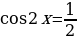 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
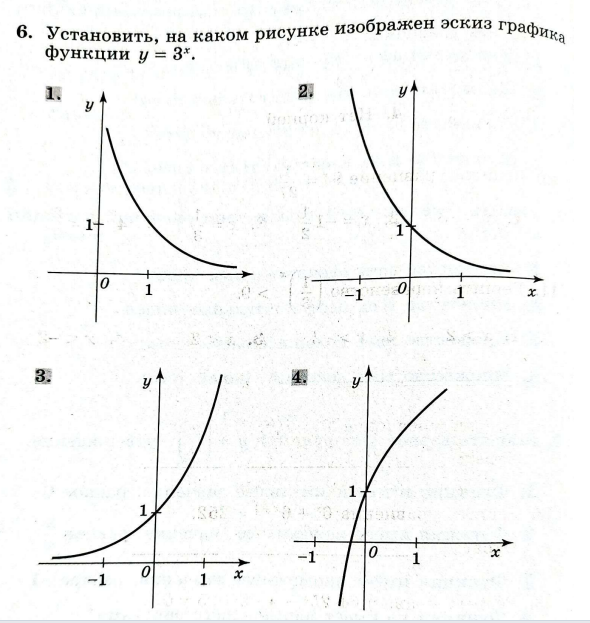
На каком рисунке изображён эскиз графика функции y = 3х.
Выполните действия 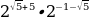 .
.
Вычислите 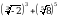 .
.
Найдите значение выражения 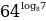 .
.
Найдите значение выражения 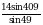 .
.
Решите уравнение 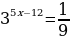 .
.
Решите уравнение 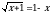 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SD = 17, АС = 16. Найдите длину отрезка SО.
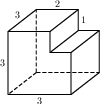
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны АВ = 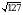 , АА1 = 4, А1D1 = 1. Найдите длину диагонали BD1.
, АА1 = 4, А1D1 = 1. Найдите длину диагонали BD1.
В сборнике билетов по биологии всего 30 билетов, в 12 из них встречается вопрос по курсу ботаники. Найдите вероятность того, что в случайно выбранном билете по биологии не окажется ни одного вопроса по ботанике.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 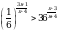 .
.
Решите уравнение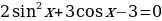 .
.
В а р и а н т 21
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 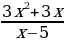
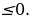
Решите неравенство 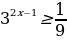 .
.
Решите уравнение 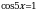 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
На каком из рисунков изображён график функции 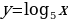 ?
?
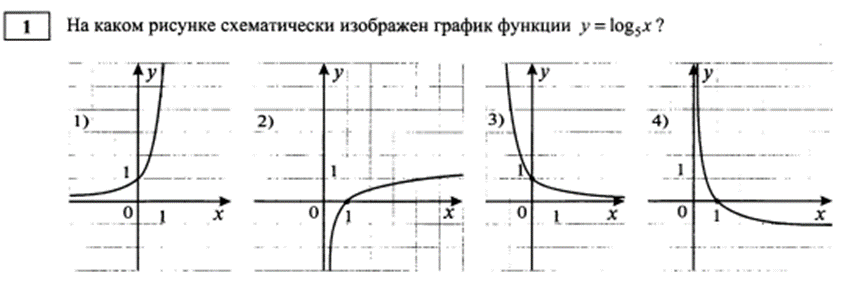
Вычислите 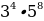 ׃
׃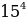 .
.
Вычислите 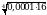 .
.
Найдите значение выражения 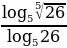 .
.
Найдите 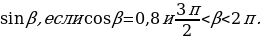
Решите уравнение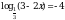 .
.
Решите уравнение 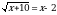 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 15, SС = 25. Найдите длину отрезка АС.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
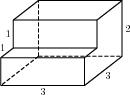
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 10.

Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 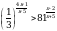 .
.
Решите уравнение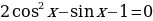 .
.
В а р и а н т 22
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 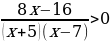 .
.
Решите неравенство 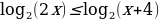 .
.
Решите уравнение 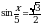 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
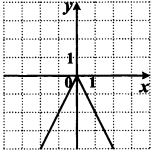
Укажите наибольшее значение функции на рисунке.
Найдите значение выражения 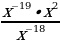 при х = 5.
при х = 5.
Вычислите 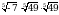 .
.
Найдите значение выражения 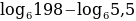 .
.
Найдите значение выражения 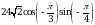 .
.
Решите уравнение 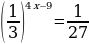 .
.
Решите уравнение 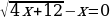 .
.
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что АВ = 6, SМ = 19. Найдите площадь боковой поверхности.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
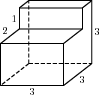
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь поверхности равна 930.

В среднем из 120 сумок, поступивших в продажу, 3 сумки имеют какой-либо скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без дефектов.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 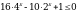 .
.
Решите уравнение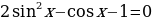 .
.
В а р и а н т 23
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 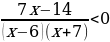 .
.
Решите неравенство 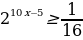 .
.
Решите уравнение 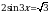 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
На каком рисунке схематически изображён график функции y = 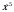 .
.

Выполните действия 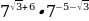 .
.
Вычислите 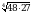 .
.
Найдите значение выражения 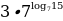 .
.
Упростите выражение 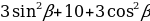 .
.
Решите уравнение 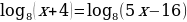 .
.
Вычислите сумму корней уравнения 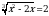 .
.
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что АВ = 6, а площадь боковой поверхности равна 171. Найдите длину отрезка SМ.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
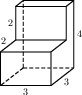
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12. Площадь ее поверхности равна 288. Найдите высоту призмы.

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 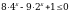 .
.
Решите уравнение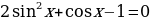 .
.
В а р и а н т 24
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 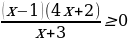 .
.
Решите неравенство 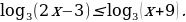
Решите уравнение 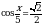 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
По графику функции, изображённому на рисунке, определите количество нулей функции.
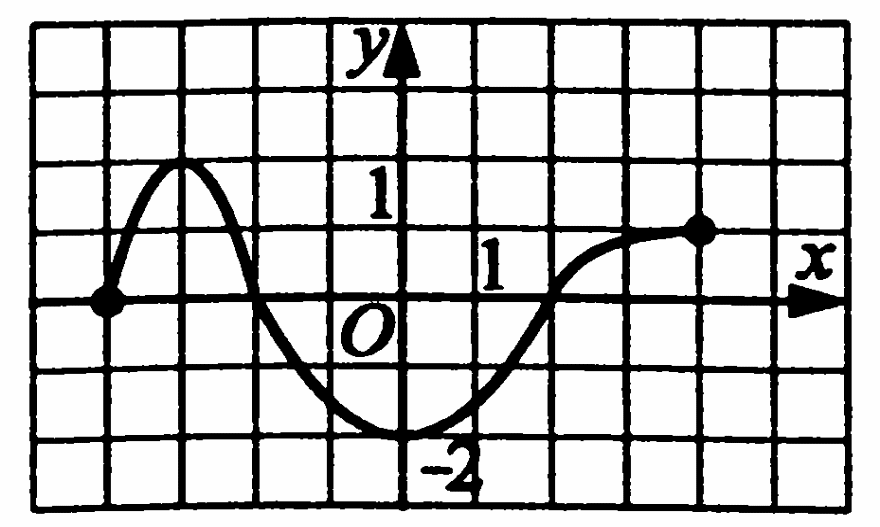
Вычислите 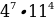 ׃
׃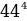 .
.
Вычислите 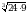 .
.
Найдите значение выражения 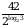
Найдите значение выражения 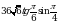 .
.
Решите уравнение 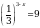
Решите уравнение 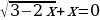 .
.
В правильной треугольной пирамиде SABC точка М – середина ребра ВС, S – вершина. Известно, что SМ = 19, а площадь боковой поверхности равна 171. Найдите длину отрезка AB.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
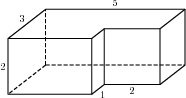
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12. Площадь ее поверхности равна 288. Найдите высоту призмы.

В среднем из 150 пар обуви, поступивших в продажу, 3 пары имеют какой-либо скрытый дефект. Найдите вероятность того, что случайно выбранная пара окажется без дефектов.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 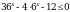 .
.
Решите уравнение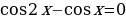 .
.
В а р и а н т 25
ЧАСТЬ 1
| Запишите решение заданий 1 – 14. |
Решите неравенство 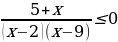 .
.
Решите неравенство 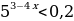
ИЛИ
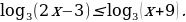
Решите уравнение 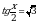 .
.
| Ответом к заданиям 4 – 14 является целое число или конечная десятичная дробь. |
График, какой функции, изображён на картинке?
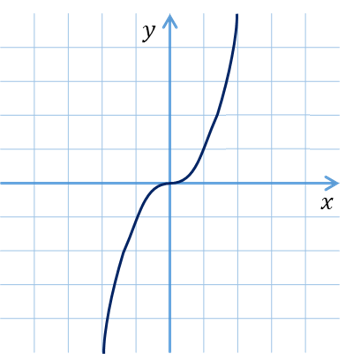
1) у = х –6 2) у = х8
3) у = х5 4) у = х –9
Найдите значение выражения 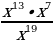 при х = 7
при х = 7
ИЛИ
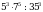 .
.
Вычислите 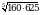 .
.
Найдите значение выражения 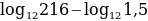 .
.
Упростите выражение 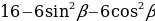 .
.
Решите уравнение 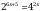
ИЛИ
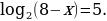
Найдите произведение корней уравнения 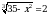
ИЛИ
Решите уравнение 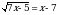 .
.
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 20, BD = 30. Найдите боковое ребро SC.
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 =  , BB1 = 5, B1C1 = 6. Найдите длину ребра A1B1.
, BB1 = 5, B1C1 = 6. Найдите длину ребра A1B1.
Гигрометр измеряет влажность в книгохранилище. Вероятность того, что влажность окажется выше 30 %, равна 0,88. Вероятность того, что влажность окажется ниже 62 %, равна 0,73. Найдите вероятность того, что влажность находится в пределах от 30 % до 62 %.
ИЛИ
Фабрика шьёт шапки. В среднем из 125 шапок, поступивших в продажу, 7 штук имеют какой-либо скрытый дефект. Найдите вероятность того, что случайно выбранная шапка окажется без дефектов.
ЧАСТЬ 2
| Запишите полное обоснованное решение и ответ заданий 15, 16. |
Решите неравенство 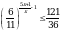
ИЛИ
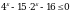 .
.
Решите уравнение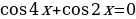 .
.






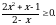
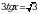 .
.
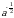 :
: 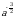 при а = 2.
при а = 2.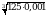
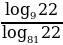 .
.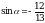 и π α .
и π α .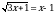 .
.
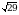 , BB1 = 2, B1C1 = 3. Найдите длину ребра АВ.
, BB1 = 2, B1C1 = 3. Найдите длину ребра АВ.
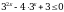 .
.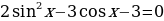 .
.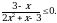
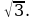
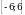 . Укажите наибольшее значение функции.
. Укажите наибольшее значение функции.
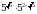 .
.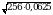 .
.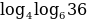 .
.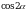 , если
, если 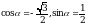 .
.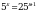 .
.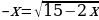 .
.
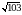 , АА1 = 3, А1D1 = 3. Найдите длину диагонали С1А.
, АА1 = 3, А1D1 = 3. Найдите длину диагонали С1А.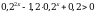 .
.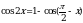 .
.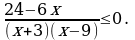
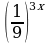
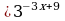 .
.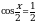 .
.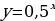 .
.
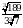 .
.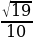 и
и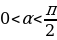 .
.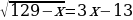 .
.

 .
.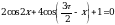 .
.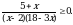
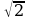 = 0.
= 0.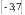 . Укажите количество нулей функции.
. Укажите количество нулей функции.
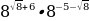 .
.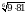
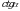 , если
, если 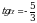 .
.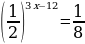 .
.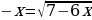 .
.

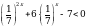 .
.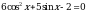 .
.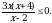
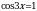 .
.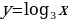 .
.
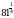 .
.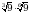 .
.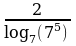 .
.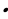 cos15°.
cos15°.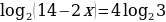 .
.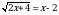 .
.

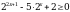 (базовый уровень).
(базовый уровень).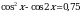 .
.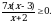
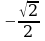 .
.
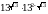 .
.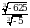 .
.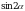 , если
, если 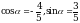 .
.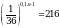 .
.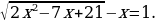


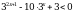 .
.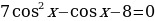 .
.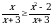 .
. .
. .
.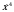 .
.
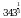 .
.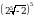 .
.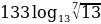 .
.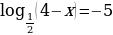 .
.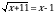 .
.
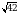 , BB1 = 4, B1C1 = 1. Найдите длину ребра А1В1.
, BB1 = 4, B1C1 = 1. Найдите длину ребра А1В1.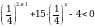 .
.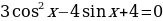 .
.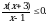
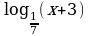 –1.
–1.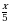 =
= 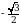 .
.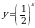 .
.
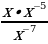 при х = 6.
при х = 6.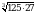 .
.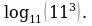
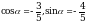 .
.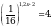
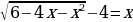 .
. 
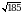 , АА1 = 2, А1D1 = 6. Найдите длину диагонали С1А.
, АА1 = 2, А1D1 = 6. Найдите длину диагонали С1А.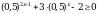 .
.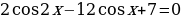 .
.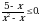
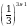
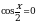 .
.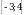 . Укажите наименьшее значение функции.
. Укажите наименьшее значение функции.
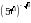 .
.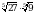 .
.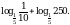
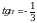 .
.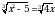 .
. 

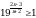 (базовый уровень).
(базовый уровень).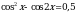 .
.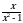
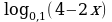 ≥ –1.
≥ –1.
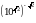 .
.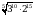 .
.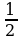 .
.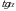 , если
, если 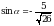 и
и 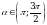 .
.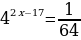 .
.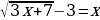 .
.

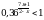 .
.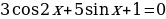 .
. 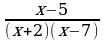 0.
0.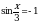 .
.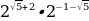 .
.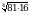 .
.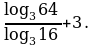
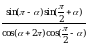 .
.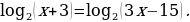
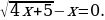

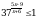 .
.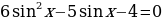 .
.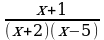 0.
0.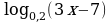 ≥ –1.
≥ –1.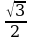 = 0.
= 0.
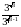 .
.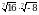 .
.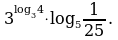
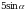 , если
, если 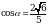 и
и 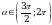 .
.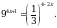
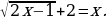


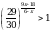 .
.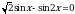 .
.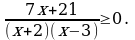
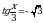 .
.
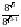 .
.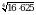 .
.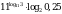 .
.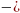 6) = 2.
6) = 2.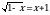 .
.
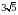 , BB1 = 2, А1D1 = 5. Найдите длину ребра DC.
, BB1 = 2, А1D1 = 5. Найдите длину ребра DC.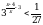 .
.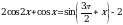 .
.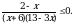
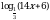 ≥
≥ 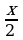 = –1.
= –1.
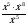 при х = 7.
при х = 7.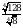 .
.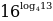 .
.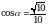 и
и 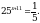
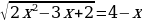 .
. 
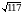 , АА1 = 6, А1D1 = 4. Найдите длину диагонали АС1.
, АА1 = 6, А1D1 = 4. Найдите длину диагонали АС1.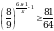 .
.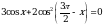 .
.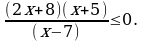
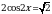 .
.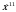 .
.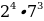 ׃
׃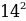 .
.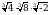 .
.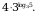
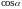 , если
, если 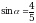 , 0 .
, 0 .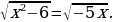

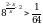 .
.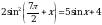 .
.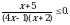
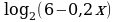 ≥ 2.
≥ 2.
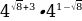 .
.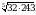 .
.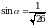 и
и 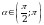 .
.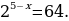
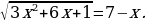

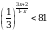 .
.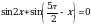 .
.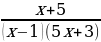
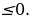
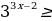
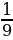 .
.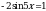 .
.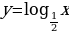 .
.
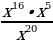 при х = 2.
при х = 2.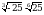 .
.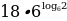 .
.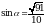 и
и 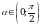 .
.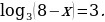
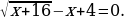

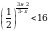 (базовый уровень).
(базовый уровень).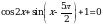 .
.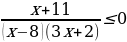 .
.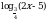
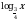 .
. 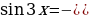
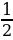 .
.
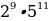 ׃
׃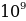 .
.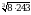 .
.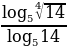 .
.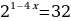 .
.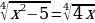 .
. 
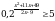 .
.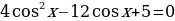 .
. 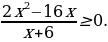
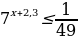 .
.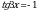 .
.
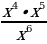 при х = 7.
при х = 7.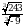 .
.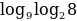 .
.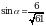 и
и 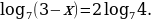
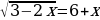 .
.
 , BB1 = 5, А1D1 = 4. Найдите длину ребра DC.
, BB1 = 5, А1D1 = 4. Найдите длину ребра DC.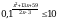 .
.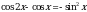 .
.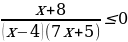 .
.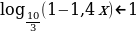 .
.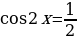 .
.
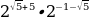 .
.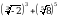 .
.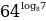 .
.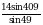 .
.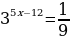 .
.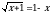 .
.
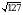 , АА1 = 4, А1D1 = 1. Найдите длину диагонали BD1.
, АА1 = 4, А1D1 = 1. Найдите длину диагонали BD1.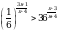 .
.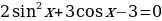 .
. 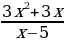
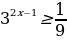 .
.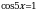 .
.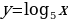 ?
?
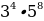 ׃
׃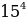 .
.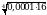 .
.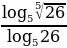 .
.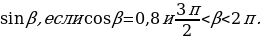
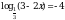 .
.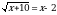 .
.
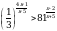 .
.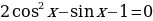 .
.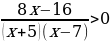 .
.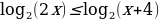 .
.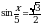 .
.
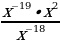 при х = 5.
при х = 5.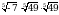 .
.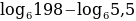 .
.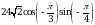 .
.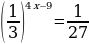 .
.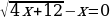 .
.
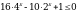 .
.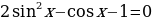 .
.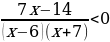 .
.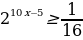 .
.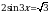 .
.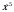 .
.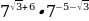 .
.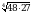 .
.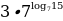 .
.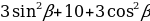 .
.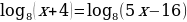 .
. .
.
 .
.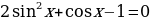 .
. .
.
 .
.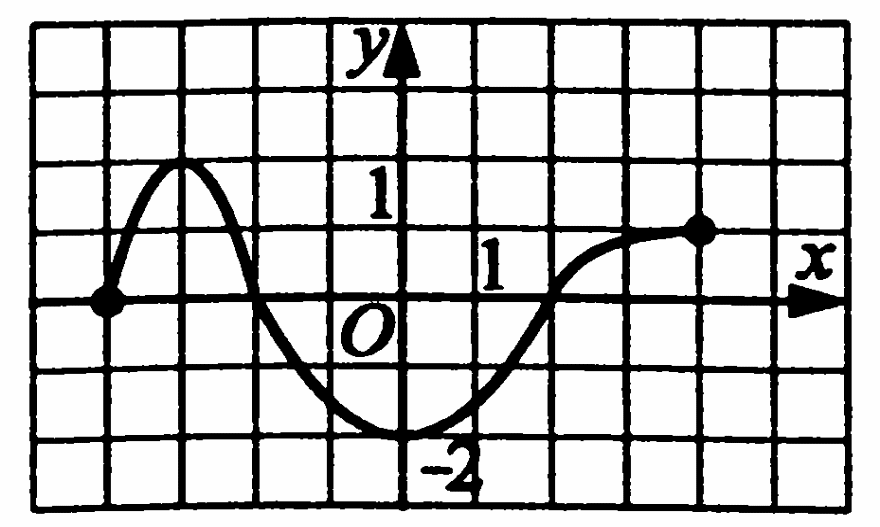
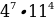 ׃
׃ .
. .
.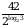
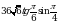 .
.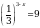
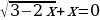 .
. 
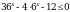 .
.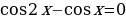 .
.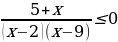 .
.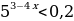
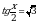 .
.
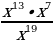 при х = 7
при х = 7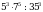 .
.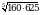 .
. 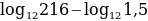 .
.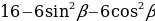 .
.
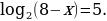
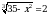
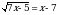 .
.
 , BB1 = 5, B1C1 = 6. Найдите длину ребра A1B1.
, BB1 = 5, B1C1 = 6. Найдите длину ребра A1B1.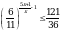
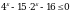 .
.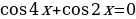 .
.









