Изучение геометрии в 8 классе. Презентация к уроку по теме "Параллелограмм".

Параллелограмм

Проектная деятельность

учащихся 8 класса

на уроке геометрии.

Косова Татьяна Анатольевна,

учитель математики

МБОУ гимназия имени А.С.Пушкина,

г.Шахты, Ростовской области

Домашний адрес: 346503 Ростовская область,

г.Шахты ул.Шоссейная 75/1 Тел.8-928-167-49-85

Адрес учебного заведения: 346500 Ростовская область,

г. Шахты, МБОУ гимназия имени А.С.Пушкина,

Пр.Победа Революции 105. тел.(8636)22-61-69.

Аннотация

Данная методическая разработка представляет собой описание опыта ее автора, связанного с применением технологии обучения геометрии с использованием интерактивной геометрической среды.

Учащиеся готовят опорные конспекты по изучаемой теме в виде слайдов презентации к каждому уроку. В конце изучения темы составляется общая презентация из лучших слайдов по данной теме. Эта презентация, как результат коллективной работы учащихся, используется при повторении и обобщении темы.

Ключевые слова

Параллелограмм. Свойства параллелограмма. Признаки параллелограмма.

ABCD -параллелограмм " width="640"

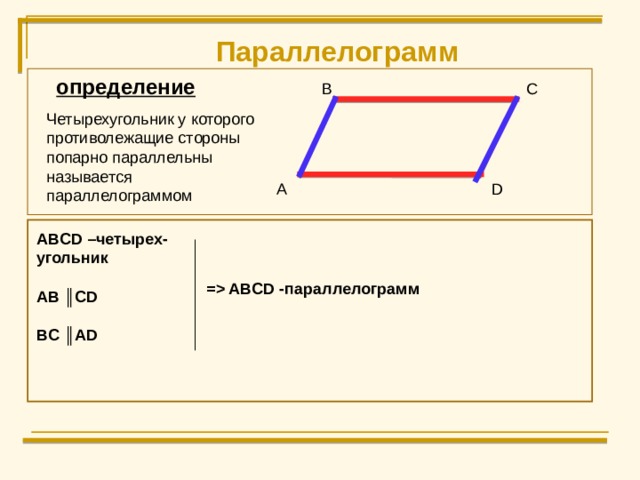
Параллелограмм

определение

С

В

Четырехугольник у которого противолежащие стороны попарно параллельны называется параллелограммом

А

D

ABCD –четырех -

угольник

AB ║CD

BC ║AD

= ABCD -параллелограмм

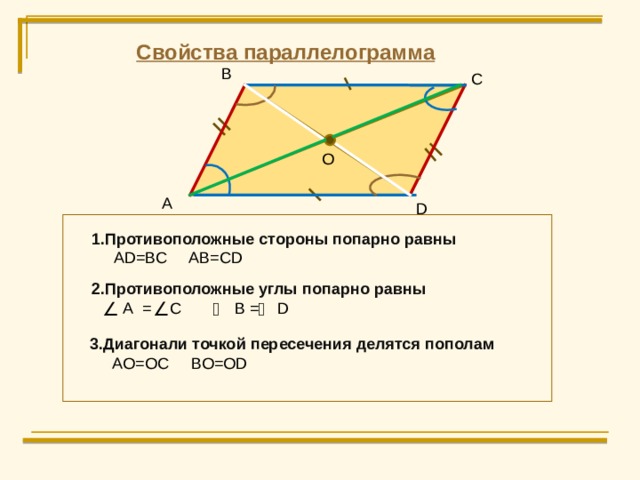
Свойства параллелограмма

В

С

O

А

D

1 .Противоположные стороны попарно равны

AD=BC AB=CD

2.Противоположные углы попарно равны

А = С В = D

3.Диагонали точкой пересечения делятся пополам

AO=OC BO=OD

Свойства параллелограмма

F

В

С

А

D

К

N

4 .Сумма смежных углов равна

А + В =

5. Биссектриса угла отсекает от него равнобедренный треугольник.

BF – биссектриса, ∆ ABF –равнобедренный, AB=BF

6 .Биссектрисы соседних углов перпендикулярны.

AF, BK – биссектрисы, AF BK

7 .Биссектрисы противоположных углов параллельны или совпадают. AF, CN – биссектрисы, AF|| CN

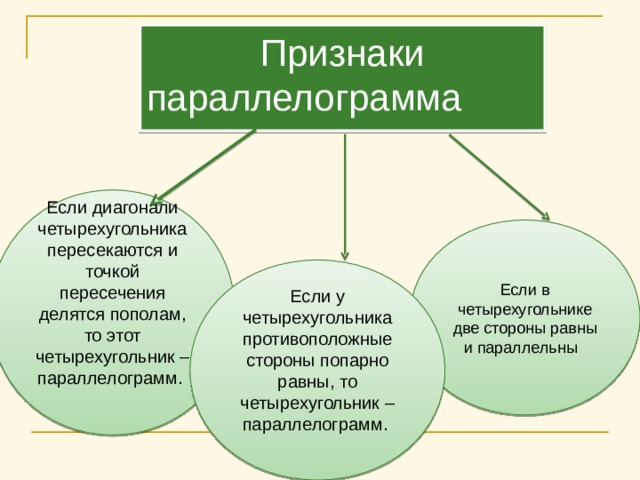
Признаки параллелограмма

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Если в четырехугольнике две стороны равны и параллельны

Если у четырехугольника противоположные стороны попарно равны, то четырехугольник – параллелограмм.

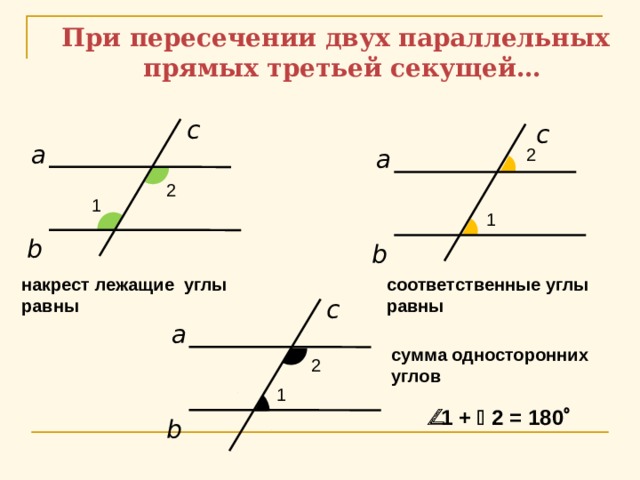
При пересечении двух параллельных прямых третьей секущей…

c

c

а

а

2

2

1

1

b

b

накрест лежащие углы равны

соответственные углы равны

c

а

сумма односторонних углов

2

1

 1 +  2 = 180 

b

ABCD- параллелограмм D А " width="640"

Признаки параллелограмма

Если в четырехугольнике противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм.

В

С

ABCD – четырехугольник

AB || CD

AB = CD

= ABCD- параллелограмм

D

А

ABCD- параллелограмм D А " width="640"

Признаки параллелограмма

Если в четырехугольнике противоположные стороны попарно параллельны, то этот четырехугольник - параллелограмм

ABCD – четырехугольник

ВС = А D

AB = CD

В

С

= ABCD- параллелограмм

D

А

ABCD- параллелограмм О А D " width="640"

Признаки параллелограмма

Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм

В

С

ABCD – четырехугольник

A О = C О

ВО = О D

= ABCD- параллелограмм

О

А

D