Тема проекта:
«Как научиться быстро считать»
Содержание
1. ВВЕДЕНИЕ
1.1 Обоснование проблемы и потребности
1.2 Цели и задачи
1.3. История возникновение счёта
-
ОСНОВНАЯ ЧАСТЬ
2.1 Приёмы и методы быстрого счёта
-
Различные способы быстрого счёта
2.3 Правила для тренировки быстрого счёта
3. ЗАКЛЮЧЕНИЕ
4. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
-
Обоснование проблемы и потребности
В настоящее время нам необходимо знать некоторые приёмы математического счёта, потому что большинство людей и в основном школьники используют калькулятор для вычислений. Не всякий ребёнок, обучаясь в школе, знает, кем он станет в будущем, но каждый понимает, что математика необходима для решения многих повседневных задач. Для проекта выбрал тему «Как научиться быстро считать» и составил план работы . Пытался найти много информации о правилах быстрого счёта. Эти правила могут пригодиться в разных жизненных ситуациях. Решением возникшей проблемы и потребности в умении хорошо считать является мой проект : «Как научиться быстро считать».
Я поставил перед собой цель работы и задачи, которые смогли бы раскрыть мои математические возможности и изучить процесс работы. Для этого требуется уделить внимание организованной отработке навыка до автоматизма.
1.2 Цели и задачи
Цель проекта: Изучить основные методы, способы и приёмы счёта, которые позволят быстро научиться считать.
Для достижения указанной цели проекта решаются следующие основные задачи:
-
Изучить тему «Как научится быстро считать»;
-
Освоить быстрый счёт и составить план работы;
-
Формирование навыков работы с различными способами;
-
Рассмотреть и найти информацию о методах быстрого счёта;
-
Выбрать необходимый подход и составить памятку.
1.3 История возникновение счёта
В истории математики выделяются несколько этапов развития знаний:
-
Способы счёта являлись (пальцы на руках, камешки, нарисованные черточки, зарубки на деревьях т.п.);
-
Появление счёта – измерения, которые позволили сравнивать длину, площади, числа;
-
Изобретение арифметических действий путём различных методом знаний;
-
Возникновения десятичной системы исчисления;
-
Изобретение счетной машины
Потребность человека в счёте стала просто необходима, первоначально использовали изображение с помощью количества чёрточек, палочек и составление предметов. Затем для изображения стали использовать буквы или специальные знаки, что привело к тому, что люди стали постепенно использовать числа «один, два, три и т.д.».
Древние цивилизации использовали математические действия. В Древнем Вавилоне писали на глиняных табличках.

Вавилонские математические тексты использовали шестидесятеричную систему счисления, которое представляла собой учебное пособие, включая умножения для чисел.
В Вавилоне впервые появляется последовательная позиционная нумерация. Первые пятьдесят девять чисел записывались с повторением знаков единиц и десятков нужное число раз. Аналогичным образом записывались числа, кратные шестидесяти, слева от первого набора. Древний народ майя вместо самих цифр рисовал страшные головы, как у пришельцев, и отличить одну голову – цифру от другой было очень сложно.
Индейцы и народы Древней Азии при счете завязывали узелки на шнурках разной длины и цвета.
И это продолжалось до тех пор, пока древние индийцы не изобрели для каждой цифры свой знак.

Арабы были первыми, кто заимствовал цифры у индийцев, и привез их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так.

Они похожи на многие наши цифры. Арабы нуль, или “пусто”, называли “цифра”. С тех пор и появилось слово “цифра”. Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся.
Десятичную систему счисления ввели римляне.
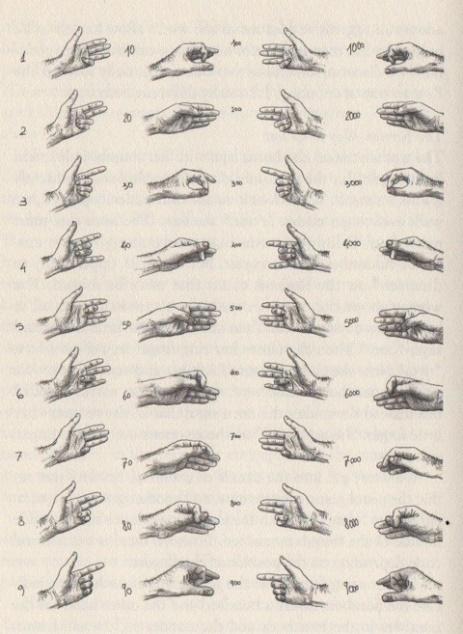
Римские цифры до сих пор используют в часах и для оглавления книг, но такая система цифр тоже была слишком сложной для счета.
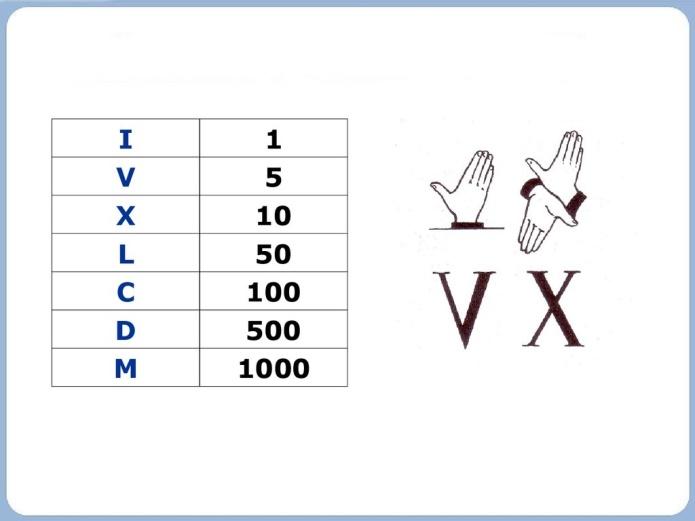
Предки русского народа – славяне - для обозначения чисел употребляли буквы.
Этот способ обозначения цифр называется цифирью
Для обозначения больших чисел славяне придумали свой оригинальный способ:
-
десять тысяч – тьма,
-
десять тем – легион,
-
десять легионов – леодр,
-
десять леодров – ворон,
-
десять воронов – колода.
Такой способ обозначения чисел был очень неудобен.
Поэтому Петр I ввел в России привычные для нас десять цифр, которыми мы пользуемся до сих пор.
ОСНОВНАЯ ЧАСТЬ
2.1. Приёмы и методы быстрого счёта
Приёмы быстрого счёта - это простые действия алгоритмы, которые желательно довести до автоматизма. После их овладения простыми приёмами можно переходить к освоению более сложных.
Устный счёт - занятие, которым в наше время себя утруждает все меньшее количество людей, часто этот навык оправдан необходимостью постоянного практического использования. Опыт и тренировка играет важнейшую роль в развитии любых способностей. Изучив многие подходы к обучению навыку считать устно, можно выделить три основных составляющихся данного навыка:
-
Способность – умение удерживать в памяти несколько вещей одновременно к логическому мышлению;
-
Алгоритм – умение оперативно подобрать нужный и конкретной ситуации;
-
Тренировка и опыт – умение постоянные тренировки и постепенное усложнение решаемых задач, которое позволяет улучшить скорость и качество устного счёта.
Счёт на пальцах. Сегодня можно встретить людей, которое могут считать на пальцах. Называется «пальчиковой гимнастикой» . Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы - это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Например, с помощью « пальчиковой методики» приводится приём умножения на 9. Хитрость этого приёма такова:
-
Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
-
Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
-
Оставшееся количество пальцев слева будет соответствовать десяткам, справа - единицам. В нашем примере - 4 пальца слева и 5 справа. Ответ: 45.
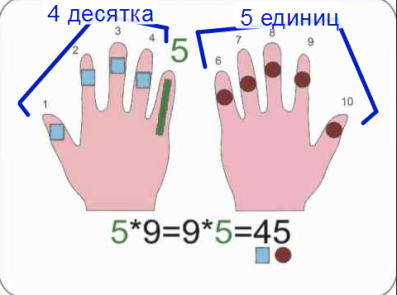
Рис.1
-
Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
-
Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. Пример: чтобы умножить 9 на 6, надо загнуть большой палец на правой руке.
-
Оставшееся количество пальцев слева будет соответствовать десяткам, справа - единицам. В нашем примере - 5 пальца слева и 4 справа. Ответ: 54
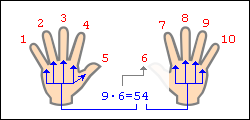
Рис.2
Счётная линейка - аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб), вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени.
Метод счёта- это быстрый счет, который часто использует способность мозга, а также развить мышление и логику.
Основных математических действий всего четыре:
-
сложение;
-
вычитание;
-
умножение;
-
деление.
У каждого действия есть свои особенности, но они не сложные.

Метод счёта
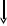


Система Трахтенберга - система состоит из набора легко запоминающихся шаблонов, которые позволяют любому быстро производить арифметические подсчёты.

Правило: Добавь цифру к её соседу. (Под соседом подразумевается цифра справа)
Пример: 3,425 × 11 = 37,675
3,425 × 11 = (0+3)(3+4),(4+2)(2+5)(5+0) = 37,675
Доказательство:
11 = 10+1
Таким образом,
3425 x 11 = 3425 x(10+1) = 34250 + 3425 = 37675

2.2 Различные способы быстрого счёта
Существует много приемов упрощения арифметических действий, но хотим остановиться на способах сложения, вычитания, умножения, деления, для производства которых достаточно устного счёта.
Способы быстрого счёта
| Способы быстрого счёта | Формулы | Пример |
| Сложное умножение | можно перегруппировать их, чтобы получился ответ:
| 40*125 все равно, что: 20*250 все равно, что: 10*500 все равно что: 5*1000 = 5000 |
| Способы быстрого сложения и вычитания натуральных чисел: | если одно из слагаемых уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится. | 429-335=(429-5)-(335+5)=424-340=84 529-435=(529-5)-(435+5)=524-440=84 |
| Деление на 5, на 50, на 25
| a:5= a ∙ 2:10 a:50=a ∙ 2:100 a:25=a ∙ 4:100
| 15:5=15 ∙ 2:10=30:10=3 1550:50=1550 ∙ 2:100=3100:100=31 2975:25=2975 ∙ 4:100=11900:100=119 |
| Умножение на 5, на 50, на 25, на 125
| a ∙ 5=a ∙ 10:2 a ∙ 50=a ∙ 100:2 a ∙ 25=a ∙ 100:4 а ∙ 125=а ∙ 1000:8
| 17 ∙ 5=17 ∙ 10:2=170:2=8543 ∙ 50=43 ∙ 100:2=4300:2=2150 27 ∙ 25=27 ∙ 100:4=2700:4=675 96 ∙ 125=96:8 ∙ 1000=12 ∙1000=12000 |
| Увеличение и уменьшение суммы | (a+b)-(a-b)=2b (a+b)+(a-b)=2a | (7+2)-(7-2)=2∙2=4 (7+2)+(7-2)=7∙2=14 |
| Быстрое возведение в квадрат |
| 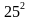 = (2 ∙ (2+1)) добавляем 25 = (2 ∙ (2+1)) добавляем 25
2∙3 = 6. В ответе получаем 625 |
2.3 Правила для тренировки быстрого счёта
Приемы весьма активно использовал и пропагандировал в своей писательской деятельности Э. Хемингуэй.
Возьмите себе за правило для начала 5-7 или даже менее вычислений в день, но старайтесь выполнять их с удовольствием и неукоснительно! Не увеличивайте нагрузку чаще раза в неделю. Попробуйте сделать эти вычисления фоном для других занятий. При спокойном и положительном эмоциональном фоне скорость и объем вычислений возрастут достаточно быстро сами собой.
Для лучшего и плавного привыкания к особенностям нагрузки при устном счете советую сначала проделать это упражнение так: записывать на бумаге условия конкретного вычисления, глядя на него, производить устный расчет, и записывать итог на бумагу (для возможности проверки). При таком подходе на начальном этапе легче набирать объем вычислений в расчете на день.
Важный признак и критерий — завершать ваши занятия, когда еще сохраняется усердие на их продолжение. Это весьма способствует созданию здорового психологического настроя в работе. Если вы будете ему следовать, каждый миг занятий сможет стать для вас творчеством, познанием, увлекательной игрой, в которую хочется играть все больше и больше.
ЗАКЛЮЧЕНИЕ
Описывая старинные способы вычислений, я попытался показать, что как в прошлом, так и в будущем, без математики, науки, созданной разумом человека, не обойтись.
В ходе работы над проектом я пришел к выводу, что данный проект будет интересен не только мне, но и тем, кто со мной учится. В процессе работы с научной литературой я обнаружил более быстрые и надежные способы вычислений. Современные способы вычислений просты и доступны всем. Мне кажется, что моя работа должна стать хорошим стимулом для знакомства учеников нашей школы с новыми способами счёта, чтобы помочь ребятам научиться пользоваться приемами вычисления без калькулятора. Приёмы вычислений были описаны в данной работе. Считаем в уме , считаем быстро, считаем правильно!.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
genius.pstu.ru/file.php/1/pupils_works_2017/Gradova_Ezhova_Romanova.pdf.
2. https://planeta.tspu.ru/files/file/1444930002.docx.
3. https://ru.wikipedia.org/wiki/Метод_Трахтенберга.
4. Катлер Э., Мак-Шейн Р.Система быстрого счёта по Трахтенбергу, 1967.
5. padabum.com › Математика.














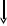




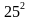 = (2 ∙ (2+1)) добавляем 25
= (2 ∙ (2+1)) добавляем 25 



















