Карта и ее математическая основа 8 класс. ФГОС.

Карта и ее математическая основа

Учитель Ребдев Н. Н.

Фигура Земли

Физическая поверхность нашей планеты имеет сложное, разнообразное строение, изменяющееся во времени. Это связано, прежде всего, с неоднородностью литосферы и горизонтальными и вертикальными движениями земной коры. Не последнюю роль в перераспределении вещества внутри Земли играют конвективные верхнемантийные и около-ядерные процессы.

В следствие этого она не может быть описана замкнутыми формулами. Но как физическое тело фигура Земли определяется через потенциальную функцию, т. е. через потенциал силы тяжести W и представляется в виде УРОВЕННОЙ ПОВЕРХНОСТИ – поверхности, во всех точках ортогональной (перпендикулярной) к отвесным линиям

Фигура Земли

Уровенная поверхность, совпадающая со средней поверхностью Мирового океана, не возмущённого приливами, течениями и разностями атмосферного давления, и продолженная под материками всюду нормально отвесным линиям, называется ОСНОВНОЙ ПОВЕРХНОСТЬЮ , а тело, ограниченное этой поверхностью, – ГЕОИДОМ .

ГЕОИД – одна из уровенных поверхностей: в любой точке она перпендикулярна направлению силы тяжести и образует, таким образом, замкнутую фигуру, принимаемую за фигуру Земли.

Фигура Земли

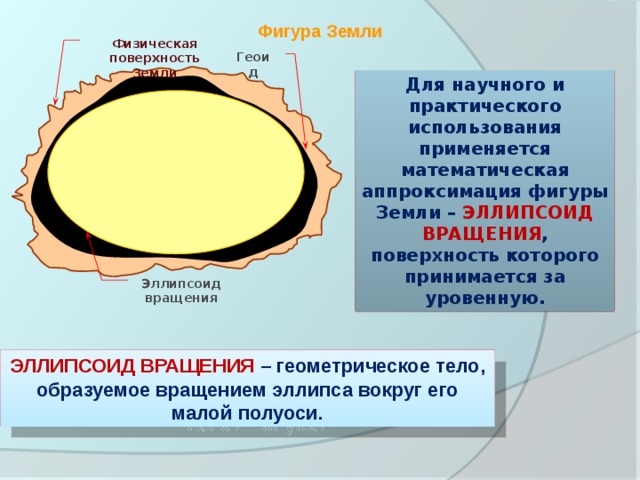
Физическая поверхность Земли

Геоид

Для научного и практического использования применяется математическая аппроксимация фигуры Земли – ЭЛЛИПСОИД ВРАЩЕНИЯ , поверхность которого принимается за уровенную.

Эллипсоид вращения

ЭЛЛИПСОИД ВРАЩЕНИЯ – геометрическое тело, образуемое вращением эллипса вокруг его малой полуоси.

Географическая карта  — изображение модели земной поверхности, содержащее координатную сетку с условными знаками на плоскости в уменьшенном виде.

Карта – это уменьшенное, математически определенное изображение земной поверхности, на которой все объекты показаны с помощью условных знаков.

Математическая основа карт – это картографическая проекция, масштаб и система координат.

Они позволяют ориентироваться по карте, производить с ее помощью измерения и вычисления.

Картографические проекции

Картографические проекции – математически определённое отображение поверхности эллипсоида или шара на плоскости карты.

В основу такого отображения картографической проекции положена система геодезических координат (B, L), координатными линиями которой являются меридианы и параллели.

Основа любой проекции – картографическая сетка – изображение сетки меридианов и параллелей на карте; по её виду одна проекция отличается от другой.

Различают следующие виды картографических сеток:

• нормальная сетка картографической проекции – картографическая сетка, получаемая в случае, когда полюс полярной системы координат совмещён с географическим полюсом;
• поперечная сетка картографической проекции – картографическая сетка, получаемая в случае, когда полюс полярной системы координат расположен на экваторе ( угол поворота полюса   равен 90° )
• косая сетка картографической проекции ( угол поворота полюса  не равный 0 и 90° )

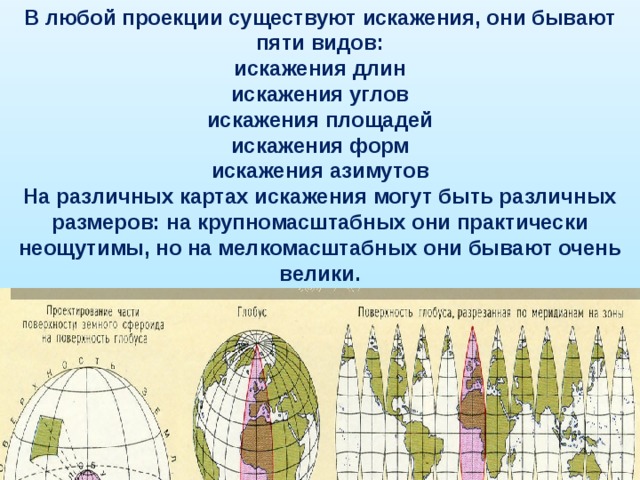
В любой проекции существуют искажения, они бывают пяти видов:

искажения длин

искажения углов

искажения площадей

искажения форм

искажения азимутов

На различных картах искажения могут быть различных размеров: на крупномасштабных они практически неощутимы, но на мелкомасштабных они бывают очень велики.

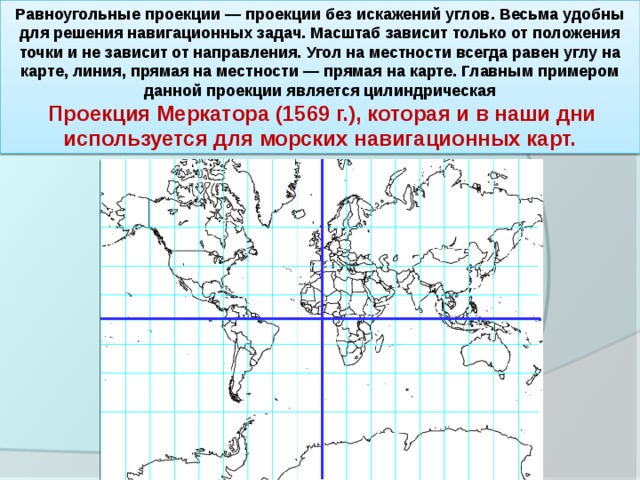
Равноугольные проекции — проекции без искажений углов. Весьма удобны для решения навигационных задач. Масштаб зависит только от положения точки и не зависит от направления. Угол на местности всегда равен углу на карте, линия, прямая на местности — прямая на карте. Главным примером данной проекции является цилиндрическая

  Проекция Меркатора (1569 г.), которая и в наши дни используется для морских навигационных карт.

В равновеликих проекциях отсутствуют искажения площадей, но при этом сильны искажения углов и форм, (материки в высоких широтах сплющиваются). В такой проекции изображаются экономические, почвенные и другие мелкомасштабные карты.

Карта мира в равновеликой проекции Мольвейде с нанесёнными эллипсами искажения

В произвольных проекциях  имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они наиболее употребляемые.

Частным случаем произвольных проекций являются  равнопромежуточные проекции , в которых сохраняются расстояния по некоторым выбранным направлениям: например, прямая азимутальная проекция, в которой правильно изображаются расстояния от полюса.

Поликонические проекции. Произвольная проекция Г. А. Гинзбурга.

Цилиндрические проекции

В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу. Таким образом задается прямоугольная сетка цилиндрических проекций

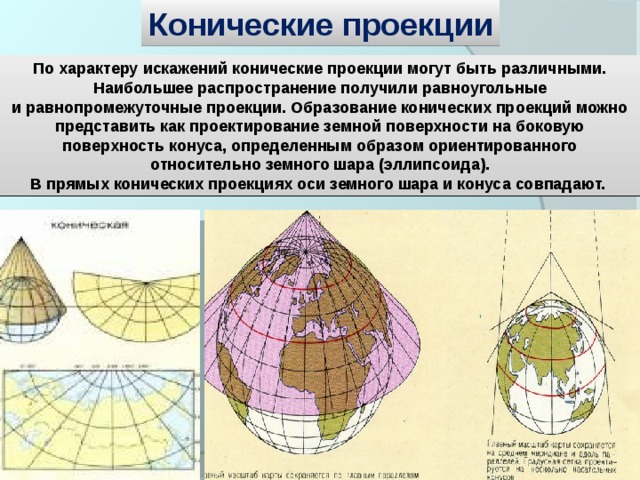
Конические проекции

По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции. Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида).

В прямых конических проекциях оси земного шара и конуса совпадают.

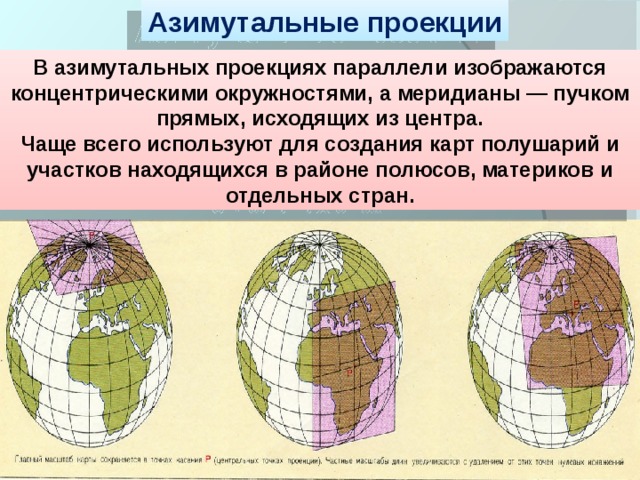
Азимутальные проекции

В азимутальных проекциях параллели изображаются концентрическими окружностями, а меридианы — пучком прямых, исходящих из центра.

Чаще всего используют для создания карт полушарий и участков находящихся в районе полюсов, материков и отдельных стран.

ДОМАШНЕЕ ЗАДАНИЕ:

Определение на основе карт атласа территорий России с наибольшими искажениями на различных картографических проекциях

§ 1