Карточка 2 по геометрии

Вариант 1

1.

Тангенс острого угла прямоугольной трапеции равен 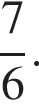  Найдите её большее основание, если меньшее основание равно высоте и равно 14.

2.  В угол C величиной 113° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.

3.

Площадь параллелограмма ABCD равна 104. Точка E  — середина стороны AB. Найдите площадь трапеции EBCD.

4.  На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

5. Укажите номера верных утверждений.

1)  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2)  Треугольник со сторонами 1, 2, 4 существует.

3)  Если в ромбе один из углов равен 90°, то такой ромб  — квадрат.

4)  Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их номера в порядке возрастания.

6. В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB  =  12.

7.

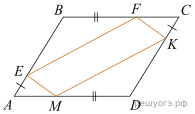
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF  =  DM, BE  =  DK. Докажите, что EFKM  — параллелограмм.

Вариант 2

1.

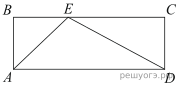
На стороне BC прямоугольника ABCD, у которого AB = 5 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.

2.  AC и BD  — диаметры окружности с центром O. Угол ACB равен 12°. Найдите угол AOD. Ответ дайте в градусах.

3. 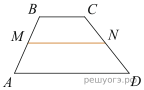 В трапеции ABCD известно, что AD  =  6, BC  =  4, а её площадь равна 80. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

4.

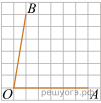
Найдите тангенс угла AOB.

5. Какие из следующих утверждений верны?

1)  Треугольника со сторонами 1, 2, 4 не существует.

2)  Сумма углов любого треугольника равна 360 градусам.

3)  Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

6.

В трапеции АВСD боковые стороны AB и CD равны, CH  — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.

7. В параллелограмме ABCD  точка    — середина стороны AB. Известно, что   . Докажите, что данный параллелограмм  — прямоугольник.