
Касательная
к окружности
Геометрия, 8 класс
К учебнику Л.С.Атанасяна
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
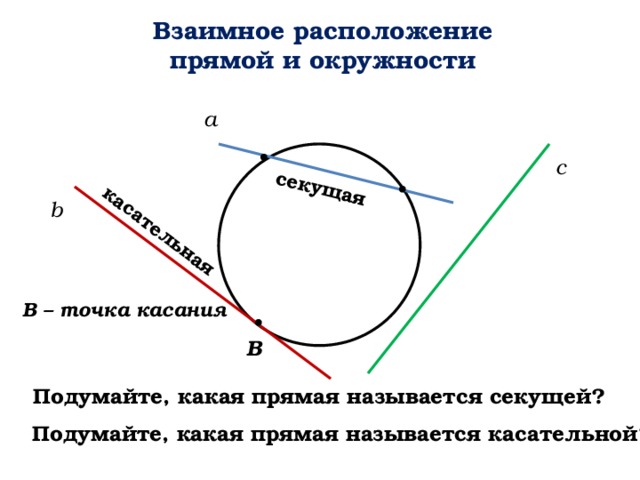
секущая
касательная
Взаимное расположение
прямой и окружности
а
c
b
В – точка касания
В
Подумайте, какая прямая называется секущей?
Подумайте, какая прямая называется касательной?
d
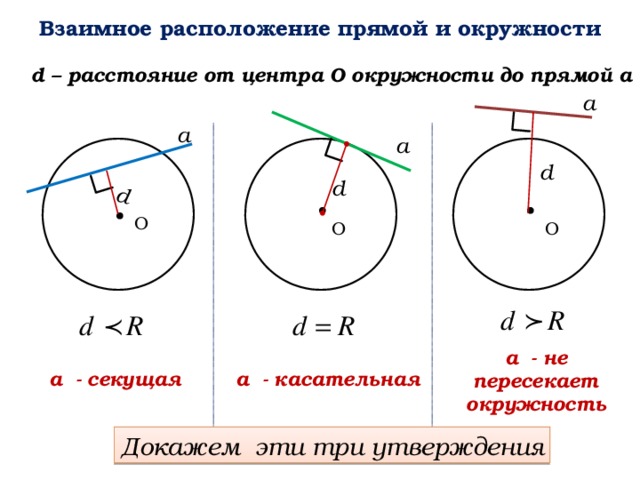
Взаимное расположение прямой и окружности
d – расстояние от центра О окружности до прямой а
а
а
а
d
d
О
О
О
а - не пересекает окружность
а - касательная
а - секущая
Докажем эти три утверждения

1 случай
В
А
Н
а
d
О
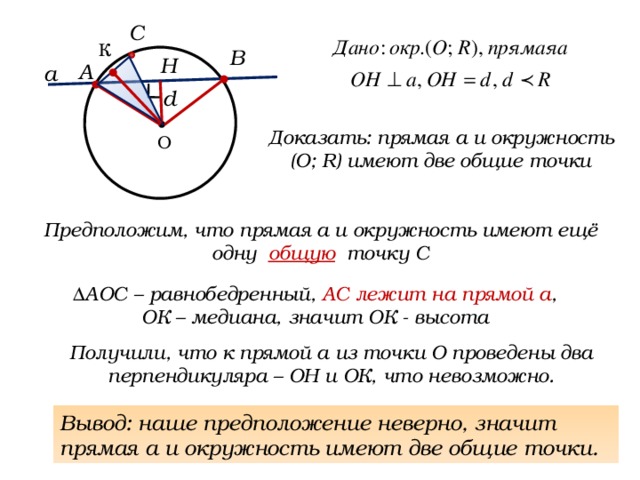
Доказать: прямая а и окружность (О; R) имеют две общие точки
Отложим на прямой а от точки Н два отрезка НВ и НА:
Проведем отрезки ОА и ОВ
Вывод: Точки A и В лежат на окружности, то есть прямая и окружность имеют две общие точки
А
С
К
В
Н
А
а
d
Доказать: прямая а и окружность (О; R) имеют две общие точки
О
Предположим, что прямая а и окружность имеют ещё одну общую точку С
ΔАОС – равнобедренный, АС лежит на прямой а ,
ОК – медиана, значит ОК - высота
Получили, что к прямой а из точки О проведены два перпендикуляра – ОН и ОК, что невозможно.
Вывод: наше предположение неверно, значит прямая а и окружность имеют две общие точки.
А
 ОН, то есть ОМ R, значит точка М не лежит на окружности. Вывод: Точка Н – единственная общая точка прямой а и окружности. А " width="640"
ОН, то есть ОМ R, значит точка М не лежит на окружности. Вывод: Точка Н – единственная общая точка прямой а и окружности. А " width="640"
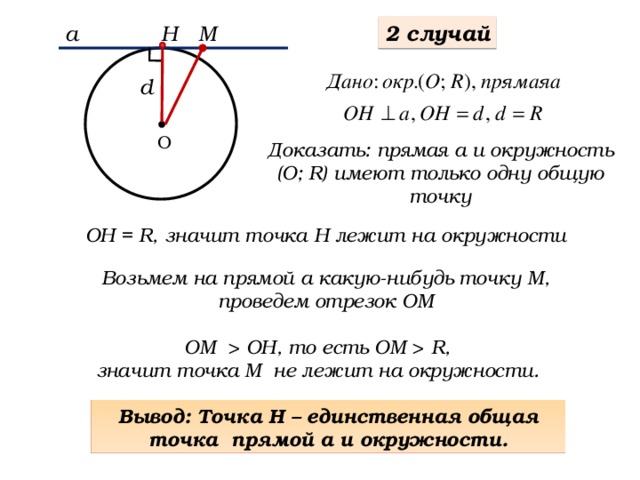
2 случай
Н
М
а
d
О
Доказать: прямая а и окружность (О; R) имеют только одну общую точку
ОН = R, значит точка Н лежит на окружности
Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ
ОМ ОН, то есть ОМ R,
значит точка М не лежит на окружности.
Вывод: Точка Н – единственная общая точка прямой а и окружности.
А
 R, значит точка Н не лежит на окружности Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ ОМ ОН R, значит точка М также не лежит на окружности Вывод: прямая а и окружность не имеют общих точек. А " width="640"
R, значит точка Н не лежит на окружности Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ ОМ ОН R, значит точка М также не лежит на окружности Вывод: прямая а и окружность не имеют общих точек. А " width="640"
Н
М
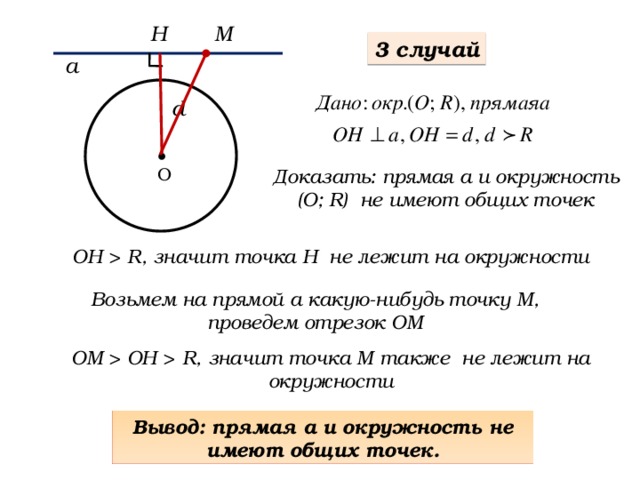
3 случай
а
d
О
Доказать: прямая а и окружность (О; R) не имеют общих точек
ОН R, значит точка Н не лежит на окружности
Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ
ОМ ОН R, значит точка М также не лежит на окружности
Вывод: прямая а и окружность не имеют общих точек.
А

Касательная к окружности
А
а
С
c
В
b
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойство касательной к окружности
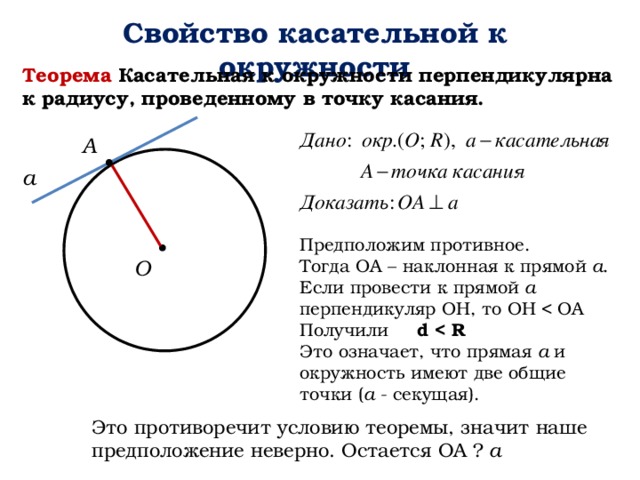
Теорема Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
А
а
Предположим противное.
Тогда ОА – наклонная к прямой а .
Если провести к прямой а перпендикуляр ОН, то ОН
Получили d
Это означает, что прямая а и окружность имеют две общие точки ( а - секущая).
О
Это противоречит условию теоремы, значит наше предположение неверно. Остается ОА ⏊ а
d
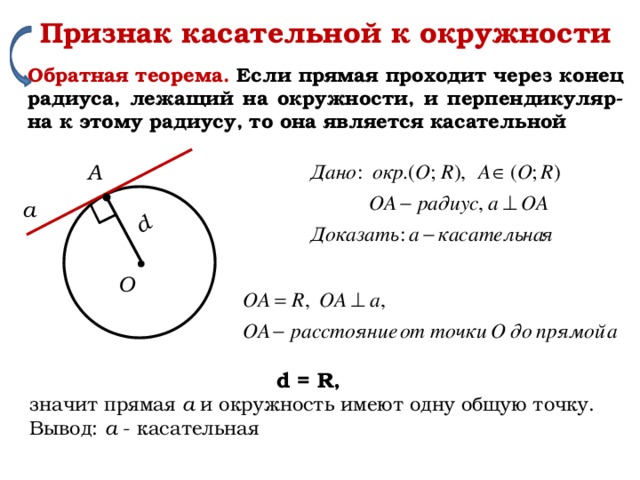
Признак касательной к окружности
Обратная теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикуляр-на к этому радиусу, то она является касательной
А
а
О
d = R,
значит прямая а и окружность имеют одну общую точку.
Вывод: а - касательная
А
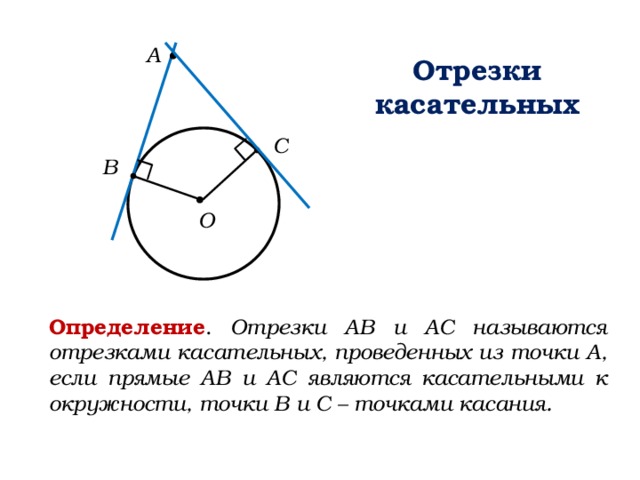
Отрезки касательных
C
B
О
Определение . Отрезки АВ и АС называются отрезками касательных, проведенных из точки А, если прямые АВ и АС являются касательными к окружности, точки В и С – точками касания.

Свойство отрезков касательных
Теорема Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
А
C
B
О
ΔBAO = ΔCAO (Почему?)
Из равенства треугольников следует …

Задача 1
А
C
76 0
О
B
СА и СВ - касательные к окружности, точки А и В – точки касания, ∠АСВ = 76 0 . Найдите величину угла АОВ.
10 см
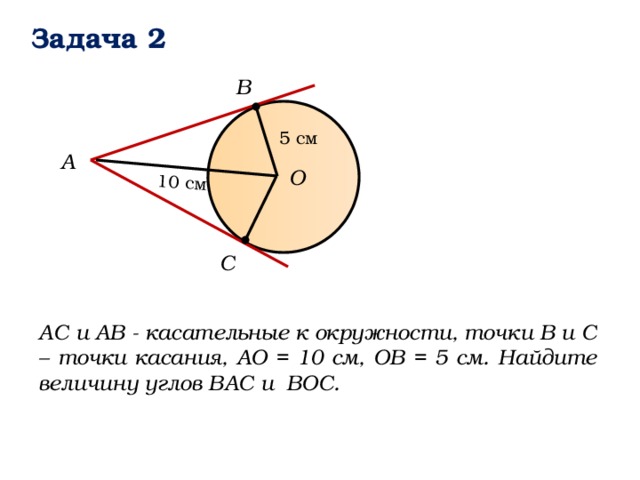
Задача 2
B
5 см
А
О
C
АС и АВ - касательные к окружности, точки В и С – точки касания, АО = 10 см, ОВ = 5 см. Найдите величину углов ВАС и ВОС.
13
12
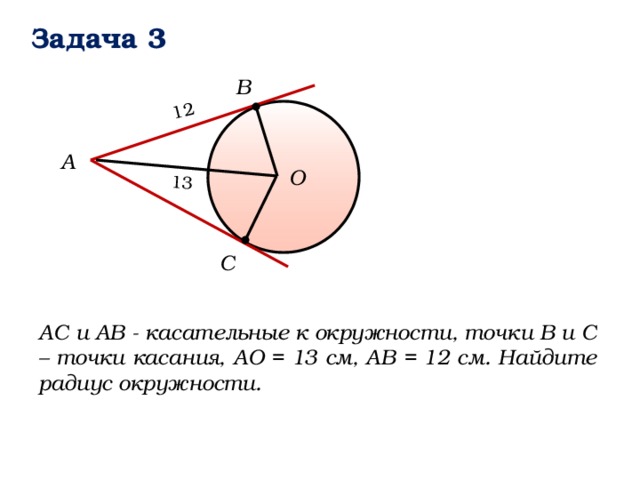
Задача 3
B
А
О
C
АС и АВ - касательные к окружности, точки В и С – точки касания, АО = 13 см, АВ = 12 см. Найдите радиус окружности.
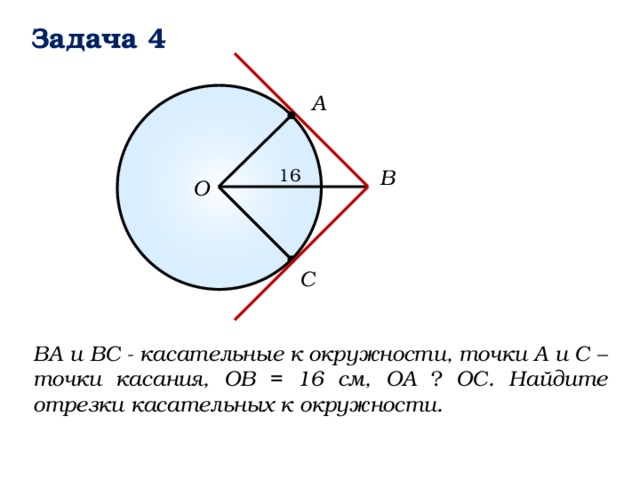
Задача 4
А
B
16
О
C
ВА и ВС - касательные к окружности, точки А и С – точки касания, ОВ = 16 см, ОА ⏊ ОС. Найдите отрезки касательных к окружности.












 ОН, то есть ОМ R, значит точка М не лежит на окружности. Вывод: Точка Н – единственная общая точка прямой а и окружности. А " width="640"
ОН, то есть ОМ R, значит точка М не лежит на окружности. Вывод: Точка Н – единственная общая точка прямой а и окружности. А " width="640"
 R, значит точка Н не лежит на окружности Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ ОМ ОН R, значит точка М также не лежит на окружности Вывод: прямая а и окружность не имеют общих точек. А " width="640"
R, значит точка Н не лежит на окружности Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ ОМ ОН R, значит точка М также не лежит на окружности Вывод: прямая а и окружность не имеют общих точек. А " width="640"




























