Классификация формул алгебры логики. Законы логики.
.
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B.
Пример.
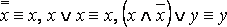 .
.
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр., 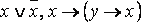 ).
).
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., 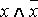 ).
).
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A↔B тавтология, и обратно, если формула A↔B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· 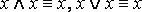 – законы идемпотентности;
– законы идемпотентности;
·  ;
;
· 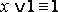 ;
;
· 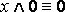 ;
;
· 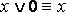 ;
;
· 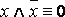 – закон противоречия;
– закон противоречия;
· 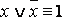 – закон исключенного третьего;
– закон исключенного третьего;
· 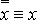 – закон снятия двойного отрицания;
– закон снятия двойного отрицания;
· 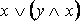
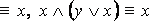 – законы поглощения.
– законы поглощения.
2. Равносильности, выражающие одни логические операции через другие:
· 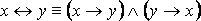 ;
;
· 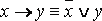 ;
;
· 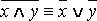 ;
;
· 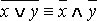 ;
;
· 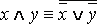 ;
;
· 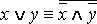 .
.
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как  не может быть выражена с помощью операции конъюнкции.
не может быть выражена с помощью операции конъюнкции.
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x|y≡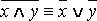 («x не совместно с y»).
(«x не совместно с y»).
Логические значения связки Шеффера описываются следующей таблицей истинности:
| x | y | x|y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Имеют место следующие равносильности: а) 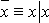 ; б)
; б) 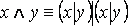 .
.
2) Стрелка Пирса – конъюнкция отрицаний.
Обозначение. x↓y≡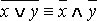 («ни x, ни y»).
(«ни x, ни y»).
Логические значения стрелки Пирса описываются следующей таблицей истинности:
| x | y | x↓y |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
3. Равносильности, выражающие основные законы алгебры логики:
· 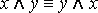 – коммутативность конъюнкции;
– коммутативность конъюнкции;
·  – коммутативность дизъюнкции;
– коммутативность дизъюнкции;
·  – ассоциативность конъюнкции;
– ассоциативность конъюнкции;
·  – ассоциативность дизъюнкции;
– ассоциативность дизъюнкции;
·  – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
·  – дистрибутивность дизъюнкции относительно конъюнкции.
– дистрибутивность дизъюнкции относительно конъюнкции.
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
2



























