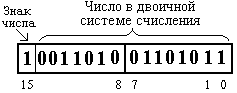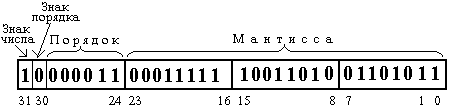Кодирование.Форматы чисел

Форматы чисел

ПОНЯТЬ

Знать, как число представляется в двоичной системе счисления важно, но не достаточно, чтобы понять, как числа хранятся в памяти компьютера. Ведь числа могут быть положительными и отрицательными, целыми и дробными, очень маленькими и очень большими. Если выбрать единственный способ представления для чисел любого вида, то или длина кода будет очень большой, или способ кодирования/декодирования будет сложным.

В современных электронных таблицах и в языках программирования используется несколько способов представления чисел. Их называют числовыми типами или числовыми форматами.

Способы представления целых чисел.

1 способ – тип byte.

Под число отводится один байт, в котором записывается целое число в двоичной системе счисления. Таким образом можно представить натуральные числа от 1 до 255 и 0.

Пример

Код 00010001 соответствует в типе byte числу 17₁₀.

Код 10010001 соответствует в типе byte числу 145₁₀.

Этот тип часто используется для счётчиков, в которых хранятся номера элементов, команд и т.п.

2 способ – тип short integer (короткое целое).

Под число тоже отводится 1 байт, но старший бит определяет знак числа, а остальные 7 бит – двоичный код числа. Если число положительное, то в старший бит заносится 1, если отрицательное, то 0.

Пример

Код 00010001 соответствует числу +17₁₀.

Код 10010001 соответствует числу –17₁₀.

Всего в таком формате можно представить тоже 256 разных чисел, но их значения будут лежать в диапазоне от -128 до +127 (код 00000000 соответствует числу 0₁₀, код 10000000 соответствует не числу –0, а –128).

3 способ – тип integer (целое)

Под число отводится 2 байта. Старший бит определяет знак числа, а остальные 15 бит – двоичный код числа.

Пример

Код 00000001 00010001 соответствует числу +273₁₀.

Код 10000001 00010001 соответствует числу –273₁₀.

Всего в таком формате можно представить 65536 разных чисел в диапазоне от –32768 до +32767.

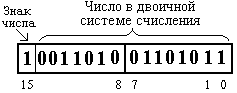
Рис. Схема представления чисел в формате integer.

4 способ – представления вещественных чисел в формат real (действительное число).

Вещественными являются такие числа как: +134,25; –100000000; +0,00013425; –0,05.

Чтобы их можно было закодировать по одному и тому же правилу, нужно привести их к какому-то одному виду. В математике для этого служит представление числа в виде с плавающей точкой:

+134,25 = +0,1342510⁺³ = +0,13425 Е +3 (буква Е в компьютерных расчетах обозначает 10, которая возводится в степень, записанную далее);

–100000000 = –0,110⁺⁹ = –0,1 Е +9;

+0,00013425 = +0,1342510^–3 = +0,13425 Е –3;

–0,05 = –0,510^–1 = –0,5 Е –1.

В записи числа в виде с плавающей точкой всегда можно выделить: знак числа, правильную десятичную дробь (мантиссу); степень основания системы счисления (порядок); знак порядка. Именно эти четыре элемента нужно отразить в двоичном коде числа.

В формате real под число отводится 4 байта. Старший байт отводится под знаки и порядок, оставшиеся 3 байта – под двоичный код мантиссы. В старшем байте самый старший бит обозначает знак числа, следующий бит – знак порядка, оставшиеся 6 бит старшего байта – двоичный код порядка.

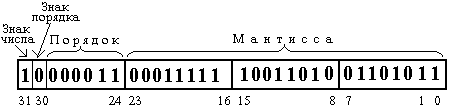
Рис. Схема представления чисел в формате real.

Пример

Код 01000100 10000000 00000000 00000000 в формате real будет интерпретироваться как +0,510^–4, то есть как +0,00005₁₀.

Код 10000011 11000000 00000000 00000000 в формате real будет интерпретироваться как –0,7510⁺³, то есть как –750₁₀.

Числа в каком диапазоне можно закодировать в данном формате? Это зависит от величины порядка. Максимальное значение порядка достигается, если все 6 бит равны 1, но 111111₂ = 63₁₀. Следовательно, в формате real можно представить числа от 10^-63 до 10⁺⁶³. Для большинства расчетов этого диапазона вполне достаточно.

Существуют и другие форматы целых и вещественных чисел, причём в каждом языке программирования, в каждой программе для числовых расчетов может быть свой набор допустимых форматов (типов).

Сегодня с увеличением производительности центрального процессора, ростом разрядности каналов передачи и ёмкости оперативной памяти под тип integer (целый) всё чаще отводят 4 байта (числа находятся в диапазоне от –2147483648 до +2147483647). Под вещественные числа типа real отводят 8 байт. При этом числа лежат в диапазоне ±1,7∙10³⁰⁸ и содержат 15-16 значащих десятичных цифр. Самое маленькое положительное число вещественного типа в таком формате равно 5,0∙10^-324. Этого с лихвой хватает для решения большинства задач. Даже в астрономии и микромире таких больших и таких маленьких результатов измерений крайне мало.

ЗНАТЬ

В современных программных средствах используются разные способы кодирования чисел. Это обусловлено разнообразием тех задач, которые требуют численных расчетов, выполняемых на компьютере.

Способы кодирования чисел называются числовыми типами или числовыми форматами.

Основными для кодирования целых чисел являются типы byte и integer.

Тип byte используется чаще всего для организации различных счетчиков. Под число отводится 1 байт, в котором хранится представление числа в двоичной системе счисления. Диапазон допустимых значений [0, 255].

Тип integer применяется, когда надо работать с положительными и отрицательными числами. Знак числа кодируется в старшем бите: 0 – положительное число, 1 – отрицательное. Всего под число отводится 2 байта (диапазон допустимых значений [–32768, +32767]) или 4 байта (диапазон допустимых значений [–2147483648, +2147483647].

Основным для кодирования вещественных чисел является тип real.

Число представляется в виде с плавающей точкой: ±0,m10^±p, где 0,m – мантисса числа, p – порядок (степень 10).

Под число в разных программах может отводиться 4 или 8 байтов.

Если под число отводится 4 байта, то старший бит используется для кодирования знака числа, следующий бит – для знака порядка, оставшиеся 6 бит старшего байта содержат двоичный код порядка числа, двоичный код мантиссы занимает 3 байта (24 бита). Такой формат позволяет закодировать числа в диапазоне 10^±63 с восемью-девятью значащими десятичными цифрами в мантиссе.

Если под вещественные числа отводится 8 байт, то под порядок и мантиссу отводится соответственно 10 и 52 бита. При этом числа лежат в диапазоне ±1,79∙10^±308 (±2^±1024) и содержат 15-16 значащих десятичных цифр в мантиссе.

УМЕТЬ

Даны два байта, содержащих числа. Декодируйте их как два числа в формате byte, как два числа в формате short integer и как одно число integer.

Даны четыре байта, содержащих числа. Декодируйте их как два целых числа формата integer и как одно вещественное число формата real.

Даны 4 байта, в которых хранятся числа (одно или несколько). Сколькими разными способами можно декодировать эту последовательность?

4