Колебательный контур. Переменный ток и его характеристики

Колебательный контур Переменный электрический ток и его характерис тики

Новосибирский колледж почтовой связи и сервиса

Разработал преподаватель НКПСиС

Стрельцов Юрий Анатольевич

Колебательный контур

СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Свободные колебания хорошо воспринимаются на примере пружинного или математического маятника, однако они могут происходить не только в механических системах, но и в электрических цепях. Одним из примеров таких цепей является колебательный LCR -контур.

Определение:

Колебательный контур (LCR-контур) — электрическая цепь, состоящая из конденсатора ёмкостью C , катушки индуктивностью L и резистора сопротивлением R . В этой цепи происходят свободные затухающие электромагнитные колебания, причём скорость затухания этих колебаний определяется сопротивлением R резистора.

Идеальный колебательный контур (LC-контур) — колебательный контур, в котором отсутствует электрическое сопротивление R . В нём происходят свободные незатухающие электромагнитные колебания.

КОЛЕБАТЕЛЬНЫЙ КОНТУР (LC-КОНТУР)

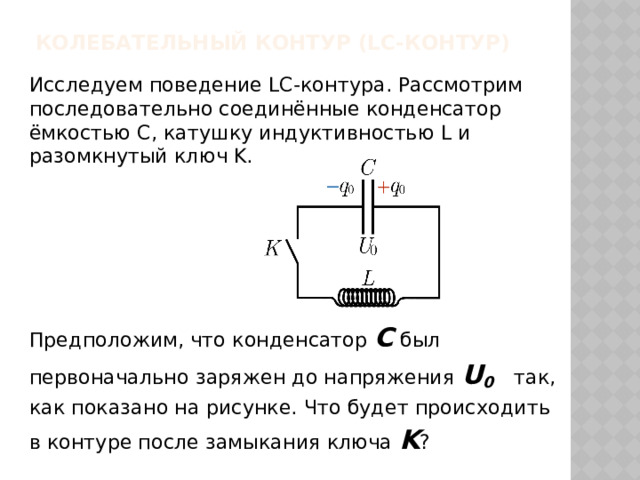
Исследуем поведение LC-контура. Рассмотрим последовательно соединённые конденсатор ёмкостью C, катушку индуктивностью L и разомкнутый ключ K.

Предположим, что конденсатор C был первоначально заряжен до напряжения U 0 так, как показано на рисунке. Что будет происходить в контуре после замыкания ключа K ?

Общий анализ

В контуре будет протекать синусоидальный ток, который будет периодически то разряжать, то заряжать конденсатор.

Рисунок Основные величины

I=(It)- сила тока в контуре

q=(qt)- заряд конденсатора

Uc= Uc(t)- напряжение на

конденсаторе

U L =U L (t) -напряжение на

катушке индуктивности

Каждая из основных величин будет изменяться по закону синуса или косинуса с циклической (собственной) частотой ω =1/

Сила тока I в контуре

Заряд q конденсатора

I= I 0 sin(ωt)

Напряжение U c на конденсаторе

q=q 0 cos(ωt)

Напряжение U L на катушке

U c =U 0 cos(ωt)

U L =U 0 cos(ωt)

Доказательство:

Первоначальный заряд конденсатора равен q 0 =U 0 C  . Сразу после замыкания ключа  K  ток в цепи не изменится скачком и будет нулевым. Это связано с наличием катушки индуктивности, в которой изменению тока воспрепятствует ЭДС самоиндукции E si  .

Напряжение U c    на конденсаторе прямо пропорционально его заряду  q , то есть U c = q/C

Напряжение U L    на катушке определяется её ЭДС самоиндукции  E si   по формуле U L= - E si= LI ’ (t) где I ’ (t) = ∆I/∆t - скорость изменения тока I   (производная тока).

Электрический ток в контуре обусловлен перетеканием заряда с одной обкладки конденсатора на другую, поэтому I = -q ’ (t)

где  q ’ (t)  = ∆q/∆t - скорость изменения заряда  q  конденсатора (производная заряда).

Получается, что  U L =-Lq ” (t) где  q ” (t) = -I ’ (t)  — вторая производная заряда  q  конденсатора.

Выводы конденсатора и катушки накоротко замкнуты друг на друга, поэтому напряжения на них равны. Выходит, что U c =U L

Последнее соотношение преобразовывается путём подстановки выражений для напряжений U c  и U L  . Получается дифференциальное уравнение гармонических колебаний, что q ” (t) + ω 2 q(t) = 0 где число  ω= 1/ называется циклической (собственной частотой колебаний).

Переменный электрический ток и его характеристики

Описание переменного тока

Определение

Переменный ток электрический ток, который с течением времени изменяет свою величину или направление.

Периодический ток переменный ток, мгновенные значения величины которого повторяются через равные промежутки времени: I = I(t) = I(t + kT)

где k любое натуральное число, Т период колебаний.

Особую роль в электродинамике играет синусоидальный (гармонический) ток, то есть электрический ток, изменяющийся по закону синуса или косинуса:

I = I(t) = I 0 (ωt + ϕ 0 )

Где I 0 - амплитуда силы тока, ϕ = ϕ(t) = ωt + ϕ 0 -фаза колебаний, ϕ 0 - начальная фаза колебаний, ω - циклическая (круговая) частота колебаний.

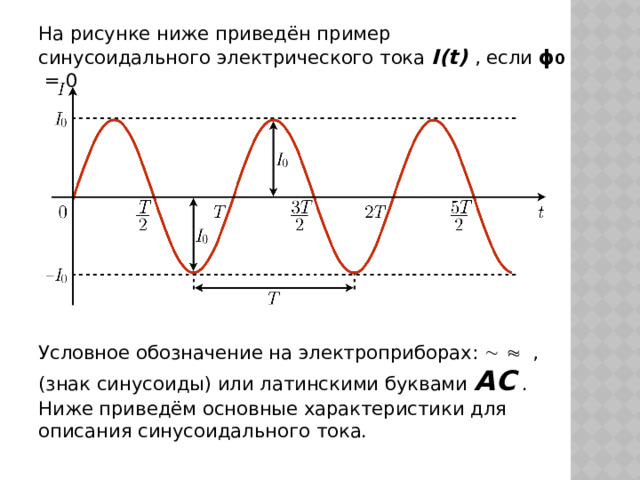
На рисунке ниже приведён пример синусоидального электрического тока I(t) , если ϕ 0 = 0

Условное обозначение на электроприборах:   , (знак синусоиды) или латинскими буквами АС . Ниже приведём основные характеристики для описания синусоидального тока.

Амплитуда колебаний I 0 силы тока I максимальное отклонение силы тока I от своего среднего значения. Размерность амплитуды колебаний той или иной физической величины совпадает с размерностью этой величины. В системе СИ единица измерения I 0 Ампер, то есть размерность [ I 0 ] = А

Циклическая частота ω колебаний силы тока I количество полных колебаний силы тока I за 2  секунд. В системе СИ единица измерения ω радиан в секунду, то есть размерность [ ω] = рад/с . Поскольку радиан безразмерная величина, то размерность циклической частоты можно представить в виде

[ ω] = c -1

Период колебаний Т силы тока I время одного полного колебания силы тока . В системе СИ единица измерения Т - секунда, то есть размерность [ Т] = c . За время, равное периоду колебаний Т , повторяется не только величина тока I , но и его направление. Он зависит от циклической частоты ω и определяется формулой Т = 2  / ω Если за время ∆t ток совершает N полных колебаний, то период Т определяется формулой Т= ∆t/N

Частота колебаний f силы тока I число полных колебаний силы тока I в единицу времени. В системе СИ единица измерения f - Герц, то есть размерность [f] =Гц. Отметим, что 1 Гц =с -1 . Если за время ∆t ток совершает N полных колебаний, то частота f определяется формулой f = N/ ∆t . Видим, что частота f является величиной, обратной периоду колебаний T , то есть f = 1/T = ω/ 2 

В задачах синусоидальный ток может быть представлен различным образом.

Формы представления

Пример 1. Аналитическое представление I(t)

Через проводник протекает переменный электрический ток. Сила тока I изменяется со временем t по закону I=2sin (  /4*t) , где все величины выражены в СИ. Определить амплитуду колебаний силы тока. Чему равен период колебаний силы тока?

Решение:

По приведённой зависимости силы тока I от времени определяем амплитуду колебаний силы тока I 0 и циклическую частоту колебаний ω . Видим, что I 0 =2A и ω =  /4 c -1

, поскольку по условию все коэффициенты выражены в СИ. Период колебаний T силы тока определяется формулой T=2  / ω, откуда T=8c. Ответ: амплитуда I 0 =2A; период T=8c

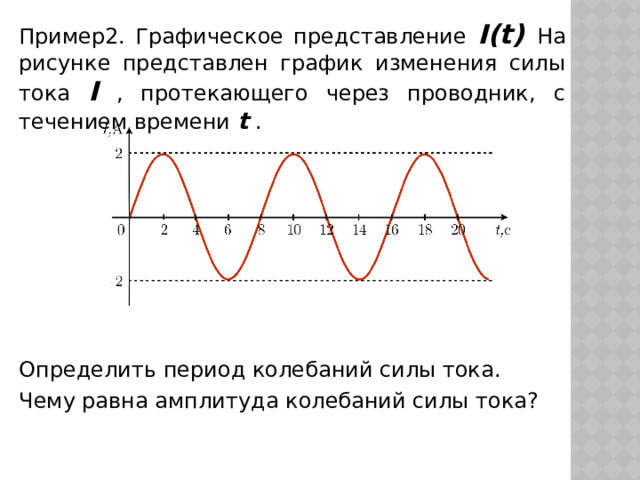
Пример2. Графическое представление I(t) На рисунке представлен график изменения силы тока I , протекающего через проводник, с течением времени t .

Определить период колебаний силы тока.

Чему равна амплитуда колебаний силы тока?

Решение:

Из графика видно, что время одного полного колебания силы тока I равно восьми секундам, то есть период колебаний силы тока T =8c

По графику определяем максимальное отклонение силы тока от среднего значения. Видим, что оно равно двум амперам, то есть амплитуда колебаний силы тока I 0 =2A

.

Пример 3. Табличное представление I(t)

В электрической цепи происходят синусоидальные колебания тока. В таблице показано, как изменялась сила тока I с течением времени t .

I,A

t,c

0

0

1,4

2

1

1,4

2

3

0

-1,4

4

5

-2

6

-1,4

7

0

8

Решение:

Из таблицы видно, что время одного полного колебания силы тока равно восьми секундам, то есть период колебаний силы тока

Т=8с . По таблице определяем максимальное отклонение силы тока I от среднего значения. Видим, что оно равно двум амперам, то есть амплитуда колебаний силы тока I 0 =2A.

Ответ: амплитуда I 0 =2A , период Т=8с .

Применение

В основном переменный электрический ток используют для передачи энергии по линиям электропередачи (ЛЭП) на дальние расстояния. Предпочтение переменному току объясняется тем, что тепловые потери при его передаче значительно меньше, чем при передаче постоянного. Поэтому производители электроэнергии (ГЭС, ТЭС, ТЭЦ, атомные и другие электростанции) генерируют переменный гармонический ток. Его частота стандартизирована. В разных странах она принимает различные значения. Например, в Российской Федерации f=50Гц , в США и Канаде f=60Гц

Промышленный переменный электрический ток получают при помощи электрических генераторов, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию.

СПАСИБО ЗА ВНИМАНИЕ!