Количество информации, единицы измерения информации
Мы постоянно что-то измеряем — время, длину, скорость, массу. И для каждой величины есть своя единица измерения, а зачастую несколько. Метры и километры, килограммы и тонны, секунды и часы — все это нам знакомо. А как же измерить информацию? Для информации тоже придумали единицу измерения и назвали ее бит.
В информатике используются различные подходы к измерению информации:
Содержательный подход к измерению информации. Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными Информация - знания человека ? сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику)
Алфавитный подход к измерению информации не связывает кол-во информации с содержанием сообщения. Алфавитный подход - объективный подход к измерению информации. Он удобен при использовании технических средств работы с информацией, т.к. не зависит от содержания сообщения. Кол-во информации зависит от объема текста и мощности алфавита. Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=28, то 1символ несет в тексте 8 бит информации.
Вероятностный подход к измерения информации. Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации, полученной при совершении того или иного события можно выразить формулой которую в 1948 году предложил Шеннон.
Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером и так далее.
Кодирование — преобразование информации из одной формы представления (знаковой системы) в другую.
Декодирование - обратный процесс, когда из компьютерного кода знак преобразуется в его графическое изображение.
В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре происходит кодирование знака, то есть преобразование его в компьютерный код.
| Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр (0 и 1). Т.о. все виды информации (слова, числа, рисунки, звуки, программы) в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц. По этой причине в вычислительной технике для двоичных знаков 0 и 1 принят специальный термин - бит. Бит — bit (от английского binary digit — двоичный знак). Каждая цифра машинного двоичного кода несет количество информации, равное одному биту. |
Количество информации - это мера уменьшения неопределенности.
1 БИТ – такое кол-во информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. БИТ- это наименьшая единица измерения информации. Единицы измерения информации: 1байт = 8 бит
Единицы количества информации
| Измерения в байтах |
| Десятичная приставка | Двоичная приставка |
| Название | Символ | Степень | Название | Символ | Степень |
| | МЭК | ГОСТ | |
| байт | B | 100 | байт | B | байт | 20 = 8 бит |
| килобайт | kB | 103 | кибибайт | KiB | Кбайт | 210 = 1024 байта |
| мегабайт | MB | 106 | мебибайт | MiB | Мбайт | 220 = 1024 Кбайта |
| гигабайт | GB | 109 | гибибайт | GiB | Гбайт | 230 = 1024 Мбайта |
| терабайт | TB | 1012 | тебибайт | TiB | Тбайт | 240 = 1024 Гбайта |
| петабайт | PB | 1015 | пебибайт | PiB | Пбайт | 250 |
| эксабайт | EB | 1018 | эксбибайт | EiB | Эбайт | 260 |
| зеттабайт | ZB | 1021 | зебибайт | ZiB | Збайт | 270 |
| йоттабайт | YB | 1024 | йобибайт | YiB | Йбайт | 280 |
Формула Шеннона 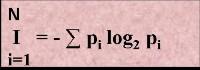
I - количество информации
N – количество возможных событий
pi – вероятности отдельных событий
Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков
1) всего шаров 50+25+25=100
2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4
3)I= -(1/2 log21/2 + 1/4 log21/4 + 1/4 log21/4) = -(1/2(0-1) +1/4(0-2) +1/4(0-2)) = 1,5 бит
Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно расcчитать по формуле 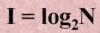
Задача2 : В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?
т.к. N = 16 шаров, то I = log2 N = log2 16 = 4 бит.
При вводе в компьютер текстовой и числовой информации происходит ее двоичное кодирование, изображение символа преобразуется в его двоичный код.
Пользователь нажимает на клавиатуре клавишу с символом, и в компьютер поступает определенная последовательность из восьми электрических импульсов (двоичный код символа). Код символа хранится в оперативной памяти компьютера, где занимает один байт.
Например, слово «МАМА» кодируется 32-разрядным двоичным числом: МАМА ® 11101101 11100001 11101101 11100001
Важно, что присвоение символу конкретного кода — это вопрос соглашения, которое фиксируется в кодовой таблице.
Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Пользователь не должен заботиться о перекодировках текстовых документов, так как это делают специальные программы-конверторы.
Кодирование информации в ПК заключается в том, что каждому символу ставится в соответствие уникальный двоичный код. Таким образом, человек различает символы по их начертаниям, а компьютер — по их кодам.
1 символ - 1 байт = 8 битов
ПРИМЕР 1.
Считая, что каждый символ кодируется одним байтом, оцените информационный объем сообщения: Без труда не вытащишь рыбку из пруда!
РЕШЕНИЕ:
Считаем количество символов в сообщении с учетом пробелов и знаков препинания. Получаем N=35. Т.к. один символ кодируется 1 байтом, то всё сообщение будет занимать в памяти компьютера 35 байт.
В настоящее время широкое распространение получил новый международный стандарт Unicode, который отводит на каждый символ не один байт, а два, поэтому с его помощью можно закодировать не 256 символов, а N = 216 = 65536 различных символов. Эту кодировку поддерживают последние версии платформы Microsoft Windows&Office (начиная с 1997 года).
ПРИМЕР 2.
Сколько места в памяти надо выделить для хранение предложения в UNICODE: Привет, Вася!
РЕШЕНИЕ:
Считаем все символы, включая знаки препинания (здесь 13 символов). В кодировке UNICODE 1 символ занимает 2 байта. Ответ: 26 байт или 208 бит
ПРИМЕР 3.
Определить информационный объем книги из 150 страниц (каждая страница содержит 40 строк, 60 символов в каждой строке).
РЕШЕНИЕ:
40 * 60 * 150 = 360 000 байт / 1024 = 351,5625 Кбайт / 1024 = 0,34332275 Мбайт
Длина фразы составляет примерно 40 символов. Следовательно, ее объем можно приблизительно оценить в 40 х 2 = 80 байт. Такого варианта ответа нет, попробуем перевести результат в биты: 80 байт х 8 = 640 бит. Наиболее близкое значение из предложенных — 592 бита. Заметим, что разница между 640 и 592 составляет всего 48/16 = 3 символа в заданной кодировке и его можно считать несущественным по сравнению с длиной строки.
Замечание: Подсчетом символов в строке можно убедиться, что их ровно 37 (включая точку и пробелы), поэтому оценка 592 бита = 74 байта, что соответствует ровно 37 символам в двухбайтовой кодировке, является точной.
Алфавит – это набор букв, символов препинания, цифр, пробел и т.п.
Полное число символов в алфавите называют мощностью алфавита
Например, мощность алфавита из русских букв = 33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел = 54 символа
ПРИМЕР 4.
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 16 символов. Второй текст в алфавите мощностью 256 символов. Во сколько раз количество информации во втором тексте больше, чем в первом?
РЕШЕНИЕ:
Если первый текст составлен в алфавите мощностью (К) 16 символов, то количество информации, которое несет 1 символ (1) в этом тексте, можно определить из соотношения: N = 2', таким образом, из 16 = 2' получим 1 = 4 бита. Мощность второго алфавита - 256 символов, из 256 = 2' получим 1 = 8 бит. Т.к. оба текста содержат одинаковое количество символов, количество информации во втором тексте больше, чем в первом, в 2 раза.