Комбинаторика и ее применение к подсчету вероятностей

Комбинаторика и ее применение к подсчету вероятностей

Дисциплины: ЕН.01 Математика,

ЕН.01 Элементы высшей математики,

2 курс

Разработчик: Латышева Н.Л.

НАВИГАЦИЯ

Содержание

Справочник

ВЫХОД

На все кнопки установлены гиперссылки.

Назад

Вперед

2

Содержание

Историческая справка

Справочник

Виды комбинаций (теория)

Алгоритм выбора решения

Практикум

Пункты содержания можно изменить (удалить или добавить). На все пункты установлены гиперссылки. Справа можно вставить рисунок, раскрывающий тему урока.

Проверь себя

Домашнее задание

3

Историческая справка Некоторые элементы комбинаторики были известны в Индии еще во 2 веке до н.э. Индийцы умели вычислять сочетания. В 12 веке Бхаскара (1114-1185) вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали сочетания в связи с применением их в поэтике – науке о структуре стиха. 2200 лет назад Архимед написал трактат «Стомахион», содержание и смысл названия которого в течение столетий были покрыты мраком. И лишь недавно историки математики обнаружили, что он содержит решение довольно сложной комбинаторной задачи. Проблема, изложенная в трактате, оказалась столь непростой, что на ее решение современными средствами потребовалось 6 недель. Комбинаторика как наука стала развиваться в 17 веке параллельно с возникновением теории вероятностей. Пищу для комбинаторных размышлений математиков давали также азартные игры и потребности секретных служб государств в развитии криптографии.

Архимед

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

Бхаскара

4

Историческая справка Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье, Г. Галилею и французским ученым Б. Паскалю и П. Ферма. В 17 в. П. Эригон и Н. Тарталья независимо друг от друга получают формулу числа сочетаний. В 1656 г. в книге «Теория и практика арифметики» А. Также посвящает сочетаниям и перестановкам целую главу. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Лейбниц вводит специальные символы и термины, выводит свойства и строит таблицы сочетаний, рассуждает о приложениях комбинаторики, предрекает ей блестящее будущее и широкое применение. В 1713 г. Я. Бернулли изучает размещения. Современная символика была предложена разными авторами в 19 в. Значительный вклад в развитие комбинаторики внес Л. Эйлер.

Лейбниц

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

Я. Бернулли

5

Комбинаторикой  называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества.  Два основных правила комбинаторики : Правило умножения  (правило « и »). Согласно ему, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару A  и  B можно выбрать  n·m  способами.  Это правило обобщается на произвольную длину последовательности. Правило сложения  (правило « или »). Оно утверждает, что, если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A  или  B можно  n + m  способами. Виды комбинаций Перестановкой  из n элементов называется каждое расположение этих элементов в определенном порядке. Размещениями  из n элементов по m называются такие выборки, которые, имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Неупорядоченные выборки называются  сочетаниями  из n элементов по m. 

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

5

Формула числа сочетаний

Пусть имеется n различных объектов. Чтобы найти число  сочетаний  из n объектов по k, будем выбирать комбинации из m объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок.

Например, есть три объекта {1,2,3}, составляем сочетания по 2 объекта в каждом. Тогда выборки {1,2} и {2,1} - это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.

На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6).

Общая формула, которая позволяет  найти число сочетаний  из n объектов по k имеет вид:

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

5

Виды комбинаций - выборки без повторений : Число перестановок  определяется по формуле  Число размещений из n элементов по m определяется по формуле  Число сочетаний  из n элементов по m определяется по формуле  Взаимосвязь между формулами: - выборки с повторениями: Число размещений из n элементов по m определяется по формуле  Число сочетаний  из n элементов по m определяется по формуле 

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

5

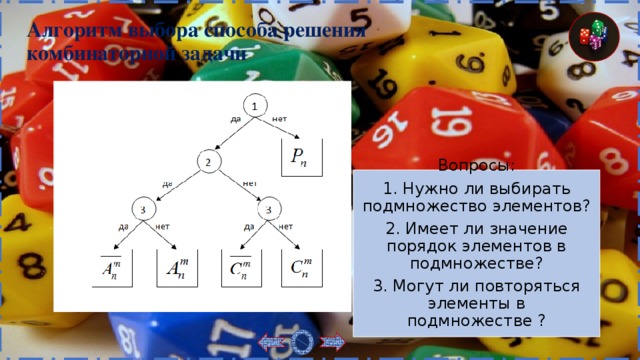
Алгоритм выбора способа решения комбинаторной задачи

Вопросы:

1. Нужно ли выбирать подмножество элементов?

2. Имеет ли значение порядок элементов в подмножестве?

3. Могут ли повторяться элементы в подмножестве ?

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Практикум Задача 1 . На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом? Задача 2 . Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг? Задача 3 . Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 30-ти книг? Задача 4 . В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные премии? Задача 5. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены одинаковые призы?

решение

решение

решение

решение

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

решение

9

Применение комбинаторики в теории вероятностей. Задача 6 . На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он  не  поставил 1-й и 2-й тома рядом? Задача 7 . На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинакового формата расположены в произвольном порядке. Читатель, не глядя, берет 3 книги. Какова вероятность того, что он взял первые три тома? Задача 8 . На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинаково оформлены и расположены в произвольном порядке. Читатель берет наугад 3 книги. Какова вероятность того, что он взял первые три тома? Задача 9 . Из аквариума, в котором 6 сазанов и 4 карпа, сачком выловили 5 рыб. Какова вероятность того, что среди них окажется 2 сазана и 3 карпа?

решение

решение

решение

решение

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 1

Определим общее число перестановок из 30 элементов по формуле  P 30 =30! Чтобы вычислить число "лишних" перестановок, сначала определим, сколько вариантов, в которых 2-й том находится рядом с 1-ым справа от него. В таких перестановках 1-ый том может занимать места с первого по 29-е, а 2-й со второго по 30-е - всего 29 мест для этой пары книг. И при каждом таком положении первых двух томов остальные 28 книг могут занимать остальные 28 мест в произвольном порядке. Вариантов перестановки 28 книг  P 28 =28! Всего "лишних" вариантов при расположении 2-го тома справа от 1-го получится 29·28! = 29!.  Аналогично рассмотрим случай, когда 2-й том расположен рядом с 1-ым, но слева от него. Получается такое же число вариантов 29·28! = 29!. Значит всего "лишних" перестановок 2·29!, а нужных способов расстановки 30!−2·29! Вычислим это значение. 30! = 29!·30; 30!−2·29! = 29!·(30−2) = 29!·28.  Итак, нам нужно перемножить все натуральные числа от 1 до 29 и еще раз умножить на 28.  Ответ:  2,4757335·10 32 .

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 2

Определим общее число размещений из 30 элементов по 15 по формуле  A 30 15  = 30·29·28·...·(30−15+1) = 30·29·28·...·16 = 202843204931727360000. Ответ:  202843204931727360000.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 3

Мы решаем эту задачу в контексте работы дизайнера интерьеров, поэтому порядок следования на полке 15-ти выбранных внешне одинаковых книг не имеет значения. Нужно определить общее число сочетаний из 30 элементов по 15 по формуле  С 30 15  =  30! /( 30  − 15)!/ 15!  = 155117520. Ответ:  155117520.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 4

Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом, так и порядком. Поскольку каждый фильм может получить призы как по одной, так и по нескольким номинациям, одни и те же фильмы могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 10 элементов по 5: 10 5 = 100 000 Ответ:  100 000.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 5

Если по каждой номинации установлены одинаковые призы, то порядок фильмов в комбинации 5 призов значения не имеет, и число вариантов представляет собой число сочетаний с повторениями из 10 элементов по 5:

Ответ:  2002.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 6

Сначала определим вероятность события А, состоящего в том, что ребенок поставил 1-й и 2-й тома рядом.  Элементарное событие - некая расстановка книг на полке. Понятно, что общее число  всех  элементарных событий будет равно общему числу всех возможных перестановок  P 30 =30!.  Число элементарных событий, благоприятствующих событию А, равно числу перестановок, в которых 1-й и 2-й тома стоят рядом. Мы рассматривали такие перестановки, решая предыдущую задачу, и получили 2·29! перестановок. Вероятность определяем делением числа благоприятствующих элементарных событий на число всех возможных элементарных событий:  P(A) = 2·29!/30! = 2·29!/(29!·30) = 2/30 = 1/15.  Событие В - ребенок  не  поставил 1-й и 2-й тома рядом - противоположно событию A, значит его вероятность P(B) = 1 − P(A) = 1−1/15 = 14/15 = 0,9333 Ответ:  0,9333.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 7

Событие A - у читателя первые три тома. С учетом порядка выбора он мог взять их 6-ю способами. (Это перестановки из 3-ёх элементов  P 3  = 3! = 1·2·3 = 6, которые легко перечислить 123, 132, 213, 231, 312, 321.)  Таким образом, число благоприятствующих элементарных событий равняется 6.  Общее число возможных элементарных событий равно числу размещений из 6-ти по 3, т.е.  A 6 3  = 6·...·(6−3+1) = 6·5·4 = 120. P(A) = 6/120 = 1/20 = 0,05.  Ответ:  0,05.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 8

Событие A - у читателя первые три тома. Это 1-й, 2-й и 3-й тома. Без учета порядка, в котором он выбирал книги, а только по конечному результату, он мог взять их одним способом. Число благоприятствующих элементарных событий - 1. Общее число возможных элементарных событий равно числу групп из 6-ти по 3, образованных без учета порядка следования элементов в группе, т.е. равно числу сочетаний  С 6 3  = 6!/3!/(6 - 3)! = 4·5·6/(1·2·3) = 4·5 = 20. P(A) = 1/20 = 0,05.  Ответ:  0,05.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Решение задачи 9

Элементарное событие - "в сачке группа из 5 рыб". Событие A - "среди 5 пойманных рыб оказалось 3 карпа 

и  2 сазана".  Пусть  n  - общее число всех возможных элементарных событий, оно равно числу способов сгруппировать по 5 рыб. Всего рыб в аквариуме 6 + 4 = 10. В процессе ловли сачком рыбы внешне неразличимы. Таким образом, "выловить 5 рыб из 10" означает сделать выборку типа сочетания из 10 по 5.  n  =  С 10 5  = 10!/5!/(10 - 5)!  Вытащив сачок и заглянув в него, мы можем определить благоприятствующий это исход или нет, т.е. состоит ли улов из двух групп - 2 сазана и 3 карпа? Группа сазанов могла сформироваться выбором из 6 сазанов по 2. Причем всё равно, кто из них первым забрался в сачок, а кто вторым, т.о. это выборка типа сочетания из 6 по 2. Обозначим общее число таких выборок  m 1  . m 1  =  С 6 2  = 6!/2!/(6 - 2)!  Аналогично общее число возможных групп по 3 карпа определяется числом сочетаний из 4 по 3. Обозначим его  m 2 . m 2  =  С 4 3  = 4!/3!/(4 - 3)!  Группы карпов и сазанов формируются в сачке независимо друг от друга, поэтому для подсчёта числа элементарных событий, благоприятствующих событию A, используем правило умножения ("и"-правило) комбинаторики. Итак, общее число благоприятствующих элементарных событий  m = m 1 ·m 2  =  С 6 2 · С 4 3   Вероятность события А определяем по формуле P(A) =  m/n = С 6 2 ·С 4 3 /С 10 5 P(A) = 6!·4!·5!·(10 - 5)!/2!/(6 - 2)!/3!/(4 - 3)!/ 10! = 5/21 ≈ 0,238 Ответ:  0,238.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Проверь себя

Вопрос 1.

В каком веке комбинаторика стала развиваться как наука?

Ответ: в 17 веке

Вопрос 2.

Какой вид комбинаций применяется в задачах, где не важен процесс формирования выборки, а важен только результат?

Ответ : сочетания

Вопрос 3.

Какое правило комбинаторики нужно применять, если необходимо найти вероятность совместного наступления двух событий?

Ответ : правило умножения (и-правило)

Вопрос 4.

Что больше и во сколько раз: (n+1)!·n или n!·(n+1)?

Ответ : первое число в n раз

Вопрос 5.

Приведите примеры областей знаний, в которых находит применение комбинаторика.

Ответ : теория вероятностей, теория игр, криптография, поэтика и др.

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Домашнее задание

Задача 1.

Сколькими способами можно выбрать четырехзначное число, все цифры которого различны?

Задача 2.

Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля?

Задача 3.

Сколько четырехзначных чисел можно записать, используя без повторений все 10 цифр?

Задача 4.

Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?

Задача 5.

В бригаде 4 женщины и 3 мужчин. Среди них разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Заголовок слайда

Здесь можно разместить теоретический материал или разобрать решение задачи. Все кнопки навигации работают.

9

Заголовок слайда

К каждой теме можно вставить рисунок или чертеж. На названиях тем установлены гиперссылки. Все кнопки навигации работают.

9

Справочник

Здесь можно разместить справочную информацию : рисунки, формулы или текст. Все кнопки навигации работают.

9

Информационные источники: Андрухаев Х.Ь. Сборник задач по теории вероятностей: Учеб. Пособие / Х.М. Андрухаев; Под ред. А.С. Солодовникова. – 2-е изд., испр. И доп. – М.: Высш. Шк., 2005. – 174 с. Кессельман В.С. Удивительная история математики / В.С. Кессельман. – М. : ЭНАС-КНИГА, 2013. – 232 с. : ил. – (О чем умолчали учебники). Фадеева Л.Н., Жуков Ю.В., Лебедев А.В. Математика для экономистов: Теория вероятностей и математическая статистика. Задачи и упражнения. – Ь.: Эксмо, 2006. – 336 с. http://mathematichka.ru/school/combinatorics/combination.html