Комбинаторные задачи

Комбинаторные задачи

Примеры комбинаторных задач.

• В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой.

• Слово «комбинаторика» происходит от латинского слова combinare , которое означает «соединять, сочетать».
• Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике и других областях знаний.

Рассмотрим некоторые комбинаторные задачи.

• Пример 1 . Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях.

• Сколько существует вариантов выбора этой пары?

Решение:

• Составим сначала все пары, в которые входит Антонов. Получим 3 пары: АГ,АС,АФ.
• Выпишем пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС,ГФ.
• Составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ.
• Других вариантов составления пар нет, так как все пары, в которые входит Федоров уже составлены.
• Итак, мы получили 6 пар: АГ,АС,АФ,

ГС,ГФ,

СФ.

• Итак, мы получили 6 пар: АГ,АС,АФ,

ГС,ГФ,

СФ.

Значит, всего существует 6 вариантов выбора тренером пары теннисистов из данной группы.

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

Пример 2.

• Сколько трёхзначных чисел можно составить из цифр 1,3,5,7 , используя в записи числа каждую из них не более одного раза?

Решение:

• Пусть на первом месте стоит цифра 1.
• На втором месте может быть записана любая из цифр 3,5 или 7 . Запишем, например, на втором месте цифру 3.
• Тогда в качестве третьей цифры можно взять 5 или 7. Получим два числа 135 и 137.
• 1
• 3
• 5 7

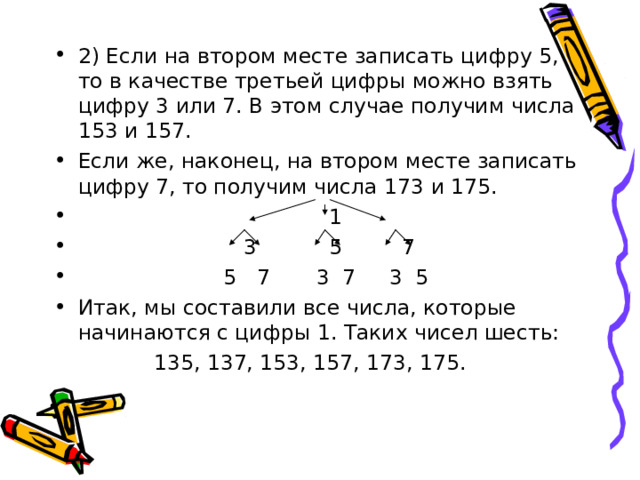
• 2) Если на втором месте записать цифру 5, то в качестве третьей цифры можно взять цифру 3 или 7. В этом случае получим числа 153 и 157.
• Если же, наконец, на втором месте записать цифру 7, то получим числа 173 и 175.
• 1
• 3 5 7
• 5 7 3 7 3 5
• Итак, мы составили все числа, которые начинаются с цифры 1. Таких чисел шесть:

135, 137, 153, 157, 173, 175.

• Аналогичным способом можно составить числа, которые начинаются с цифры 3 , с цифры 5 , с цифры 7 .
• Полученные результаты запишем в четыре строки, в каждой из которых шесть чисел:
• 135, 137, 153, 157, 173, 175.

315, 317, 351, 357, 371, 375,

513, 517, 531, 537, 571, 573,

713, 715, 731, 735, 751, 753.

Таким образом из цифр 1,3,5,7 (без повторения цифр) можно составить 24 трехзначных числа.

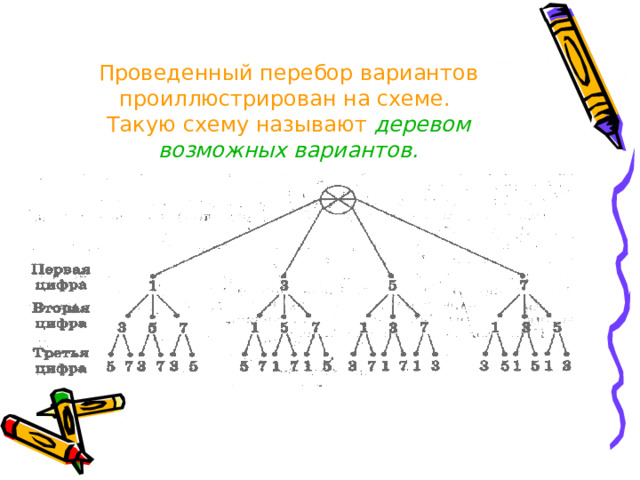
Проведенный перебор вариантов проиллюстрирован на схеме. Такую схему называют деревом возможных вариантов.

Второй способ решения.

• Ответить на поставленный вопрос в задаче можно не выписывая сами числа.

То есть путем рассуждения.

• Первую цифру можно выбрать четырьмя способами.

• Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать тремя способами.
• Наконец, третью цифру можно выбрать( из оставшихся двух) уже двумя способами.

• Следовательно, общее число искомых трехзначных чисел равно произведению 4 · 3 · 2, т.е. 24 .

• Отвечая на поставленный вопрос в задаче , мы использовали, так называемое комбинаторное правило умножения.

Общий вид комбинаторного правила умножения .

• Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов.
• Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся элементов n2 способами, затем третий элемент – n3 способами и т.д., то число способов , которыми могут быть выбраны все k элементов, равно произведению n1· n2· n3· …nk.

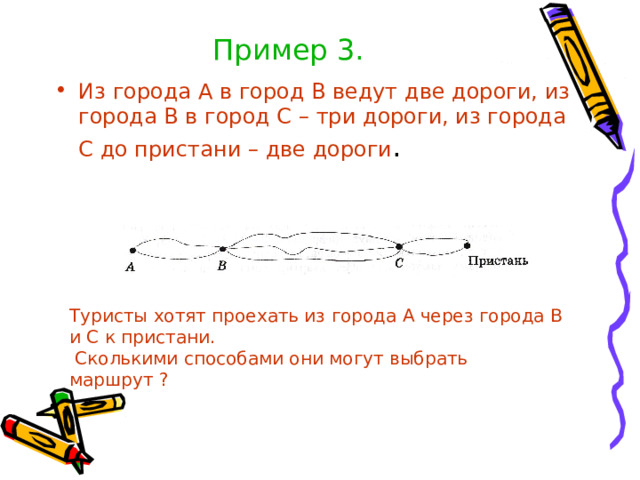
Пример 3.

• Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги .

Туристы хотят проехать из города А через города В и С к пристани.

Сколькими способами они могут выбрать маршрут ?

• Решение.

• Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеются 2 · 3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует

2 · 3 · 2, т.е. 12, способов

выбора туристами маршрута из города А к пристани.

Задача 1.

• В кафе предлагают
• два первых блюда:

борщ, рассольник –

и четыре вторых блюда:

гуляш, котлеты, сосиски, пельмени . Укажите все обеды из двух блюд, которые может заказать посетитель.

• Проиллюстрируйте ответ, построив дерево возможных вариантов.

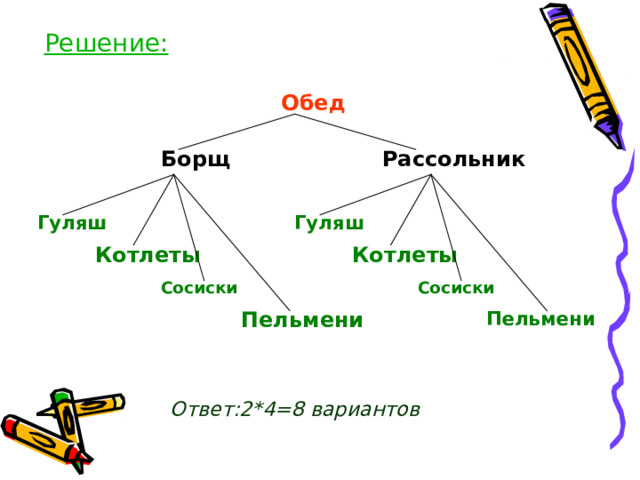
Решение:

Обед

Борщ

Рассольник

Гуляш

Гуляш

Котлеты

Котлеты

Сосиски

Сосиски

Пельмени

Пельмени

Ответ:2*4=8 вариантов

Задача 2.

• У Ирины 5 подруг:

Вера,

Зоя,

Марина,

Полина

и Светлана.

Она решила двух из них пригласить в кино.

Укажите все возможные варианты выбора подруг.

Сколько таких вариантов?

П олина

М арина

С вета

Решение

В ера

З оя

Составим сначала все пары, в которые входит Вера .

Получим 4 пары .

ВЗ, ВМ, ВП, ВС

Выпишем теперь пары, в которые входит Зоя, но не входит Вера.

ЗМ, ЗП, ЗС

Таких пар три .

Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.

МП, МС

Их две .

Далее составим пары, в которые входит Полина.

Еще одна пара

ПС

Всего существует 4+3+2+1=10

Ответ:10 вариантов

Задача 3.

• Используя цифры 0,1,3,5, составьте все возможные трёхзначные числа , в которых цифры не повторяются.

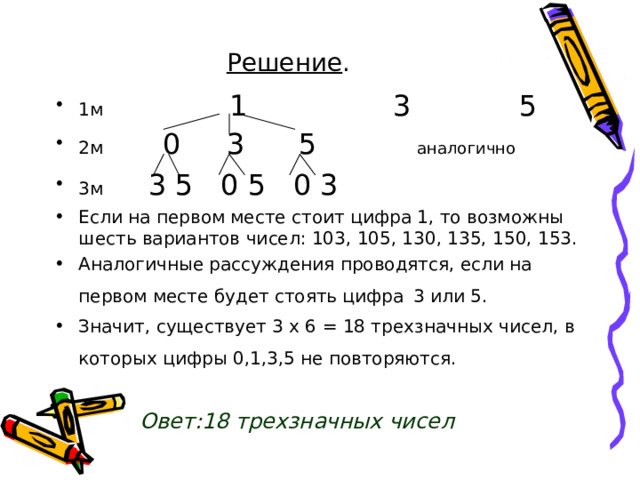
Решение .

• 1м 1 3 5
• 2м 0 3 5 аналогично
• 3м 3 5 0 5 0 3
• Если на первом месте стоит цифра 1, то возможны шесть вариантов чисел: 103, 105, 130, 135, 150, 153.
• Аналогичные рассуждения проводятся, если на первом месте будет стоять цифра 3 или 5.
• Значит, существует 3 х 6 = 18 трехзначных чисел, в которых цифры 0,1,3,5 не повторяются.

Овет:18 трехзначных чисел

Задача 4.

• В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии.

• Сколько всего партий было сыграно?

Решение.

• * * * * * * * * * ( способ перебора)

1 2 3 4 5 6 7 8 9

Первый с 8 – ю, второй с 7 – ю, третий с 6-ю, четвертый с 5-ю, пятый с 4 - мя, шестой с 3 – мя, седьмой с 2 – мя, восьмой с 1-м.

Всего 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 партий было сыграно.

Ответ: 36 партий.

Задача 5.

• Из цифр 1,2,3 составьте все возможные двузначные числа при условии, что:
• а) цифры в числе не повторяются;
• б) допускается повторение цифр в числе.

Итог:

• Комбинаторные задачи решаются тремя способами:
• 1)с помощью простого перебора;
• 2) с помощью дерева возможных
• вариантов;
• 3) по правилу умножения.
• У каждого способа есть свои преимущества и недостатки.

• Выбор решения за вами !

Домашнее задание:

• Изучить п. 30
• Решить № 716 (перебор), №720 (дерево), №727 (умножение).