| 1 | Организационно мотивационный | Слайд 1 тема урока: «размещения» - приветствие учащихся - погружение в проблемную ситуацию Слайд 2. Слайд 3- постановка проблемного вопроса. Слайд 4- термин «Комбинаторика»
- сообщение темы урока
Слайд 5- сообщение цели и задачи урока Слайд 6- выдвижение гипотезы | - приветствие учителя
- принятие темы
- формулирование собственных целей урока
- включение в работу | - настрой на урок
- мотивация к деятельности |
| 2 | Актуализация знаний | Слайд 7- Опрос учащихся по решению задачи различными способами Задача 1: Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза? (метод перебора вариантов, дерево всевозможных вариантов, правило произведения 3∙2= 6). Слайд 8,9,10 – решение задач с применением правила произведения. Задача 2: Сколько различных 3-значных чисел можно составить из цифр 3, 7 и 8 (цифры не повторяются)? 3∙2∙1=6 Задача 3: Сколько различных трёхзначных чисел можно составить из цифр 0, 6? 1∙2∙2=4 (числа)
Задача 4:Сколько различных четырёхбуквенных слов можно записать с помощью букв а) «к» и «а» (16) б) «м», «о» и «р» (81)
|
- решают предложенную задачу различными способами.
- решают предложенные задачи, делают необходимые записи.
- вносят в лист самооценки баллы за участие в опросе. | - повторение правила произведения |
| 4 | Этап «открытия» нового знания. | - Запись темы урока Слайд 13- введение в тему. Задача 1: Вы, учащиеся 11 класса изучаете по программе 12 предметов. Сколькими способами можно составить расписание уроков на один день, так чтобы было 7 разных уроков? Слайд 14- Задача-подсказка « Сколько различных двузначных чисел можно записать с помощью цифр 1,2,3,4 при условии, что в каждой записи нет одинаковых цифр?» 4 · 3 = 12 - работа с учебником стр325 вод понятия Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения. 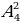 = 12 = 12 Слайд 15- вывод формулы 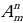 = m· (m – 1) · (m – 2) · … (m – (n -1)) (1) = m· (m – 1) · (m – 2) · … (m – (n -1)) (1) Слайд 16,17 – Задача 2,3 Задача 2: Сколькими способами можно обозначить данный вектор, используя буквы А, В, С, D, E, F? 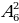 = 6 · 5 = 30 = 6 · 5 = 30
Задача 3: Решить уравнение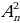 = 56 = 56 n·(n – 1) = 56 n2 – n = 56 n2 – n – 56 = 0 n1 + n2 = 1 n1 · n2 = - 56 n1 =8, n2 = -7 Т.к. n ≥ 2, то n = -7 – посторонний корень, значит n = 8.
Работа с учебником , стр 325 - Знакомство с преобразованием формулы числа размещений в формулу вида: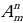 = = 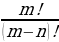 (2) (2) Слайд 18 - Закрепление применения формулы
Слайд 19
Задача 4: Вычислить: 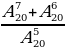 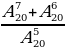 = = 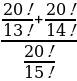 = = 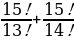 =14·15+15=15(14+1)=225 =14·15+15=15(14+1)=225
|
- делают необходимые записи
- читают определение в учебнике
- запись формулы
- учащиеся конспектируют решение задачи 2, пытаются решить задачу 3
- делают необходимые записи
- решают задачу
-знакомятся с преобразованием формулы, записывают её в тетрадь. |
- знакомство с понятием размещения
- учатся применять формулу (1)
учатся применять формулу (2) |
| 5 | Первичное закрепление изученного материала | - Решение номеров стр.325
№1072, №1073(1),№1074(1), №1075(1), №1076(1) у доски
|
- выполняют задания, ответы сверяют с данными на слайдах |
- отработка умения применения формул
|
| 7 | Постановка домашнего задания | Слайд 21. § 62, «3» №1072-1076(чёт) «4» №1077-1079(инд) «5» – Придумать свою комбинаторную задачу и решить её.
– Применение комбинаторики в практической деятельности людей. (рассказ или эссе) – Развитие комбинаторики.
| -записывают домашнее задание | - понимание домашнего задания |
| 8 | Рефлексия | Слайд 22,
- Возвращение к проблемному вопросу. «Может ли нам помочь комбинаторика в реальной жизни?» - Обсуждение гипотезы
- Оцените свою работу на уроке Слайды 23 – области применения комбинаторики. Слайды 24 -Спасибо за урок! | - отвечают на вопрос, подтверждая сферами применения комбинаторики
- учащиеся подсчитывают общее количество баллов, обмениваются информацией и производят самооценку своей деятельности. | -знание сферы практического применения темы.
Умеют правильно произвести самооценку |





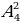 = 12
= 12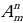 = m· (m – 1) · (m – 2) · … (m – (n -1)) (1)
= m· (m – 1) · (m – 2) · … (m – (n -1)) (1)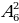 = 6 · 5 = 30
= 6 · 5 = 30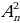 = 56
= 56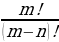 (2)
(2)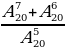
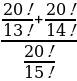 =
= 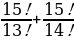 =14·15+15=15(14+1)=225
=14·15+15=15(14+1)=225









