

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 27.09.2025 17:37

Терджанян Астхик Арменовна
Преподаватель
Местоположение
Россия, Омск
Специализация
Комплекс уравнений с параметрами
Категория:
Математика
26.07.2025 12:57


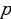 оба корня уравнения
оба корня уравнения 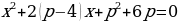 положительны.
положительны.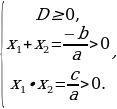
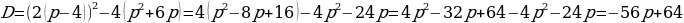
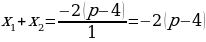
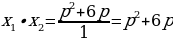
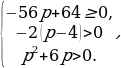
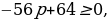
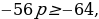
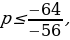
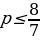
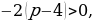
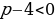 ,
,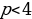
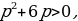
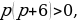
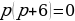
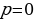 или
или 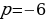
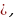 то выбираем те интервалы, где +
то выбираем те интервалы, где +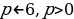

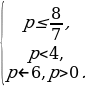
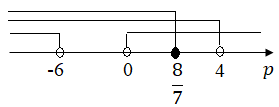
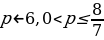 .
.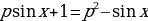 имеет хотя бы одно решение.
имеет хотя бы одно решение.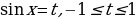
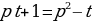 ,
,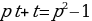 ,
,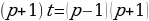
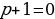 , то
, то 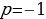 , подставляем это значение в уравнение
, подставляем это значение в уравнение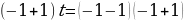
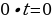 , откуда
, откуда 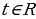 или, что то же самое,
или, что то же самое, 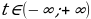
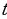 было введено ограничение, поэтому уравнение
было введено ограничение, поэтому уравнение 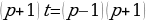 будет иметь решение при
будет иметь решение при 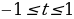
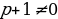 , то
, то 
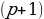
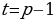
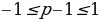 , т.е.
, т.е. 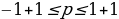 , имеем
, имеем 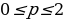
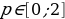 уравнение
уравнение 









