Просмотр содержимого документа
«Комплексные числа»
Практикум по математике на тему:
Практическое применение комплексных чисел
Цель практикума:
Научиться применять комплексные числа в различных практических задачах, используя алгебраические и тригонометрические представления.
Основные понятия:
1. Алгебраическая форма комплексного числа: z = a + bi, где a — действительная часть, b — мнимая часть, 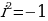 .
.
2. Тригонометрическая форма комплексного числа:
z = r(cos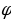 +
+ 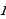 sin
sin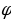 ),
),
где r — модуль, 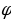 — аргумент.
— аргумент.
3. Действия над комплексными числами в алгебраической форме: сложение, вычитание, умножение, деление.
4. Перевод комплексного числа из алгебраической формы в тригонометрическую форму.
5. Модуль комплексного числа: |z| = 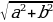 .
.
6. Умножение комплексных чисел в тригонометрической форме:
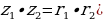
План работы:
Часть 1: Теоретический обзор
1. Понятие комплексного числа:
- Определение комплексного числа.
- Геометрическая интерпретация комплексных чисел на комплексной плоскости.
2. Алгебраическая и тригонометрическая формы:
- Преобразования между формами.
- Использование модуля и аргумента.
3. Действия над комплексными числами:
- Сложение и вычитание.
- Умножение и деление.
Часть 2: Практика
Задания:
1. Перевод из одной формы в другую:
Задача: Запишите комплексное число z = 3 + 4i в тригонометрической форме. Найдите модуль и аргумент числа.
2. Умножение и деление комплексных чисел:
Задача: Вычислите произведение двух комплексных чисел в тригонометрической форме:
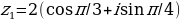
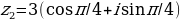
3. Решение уравнений с комплексными числами:
Задача: Решите уравнение 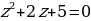 .
.
4. Определите ток в цепи переменного тока, используя комплексные числа.
Условие задачи:
Имеется цепь переменного тока, состоящая из резистора R = 5 , индуктивности L = 0.01Гн и емкости C = 0.002 Ф. Напряжение в цепи изменяется по закону u(t) = 50 cos (500t) В. Определите ток в цепи, используя комплексные числа.






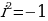 .
.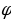 +
+ 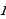 sin
sin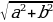 .
.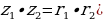
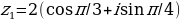
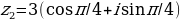
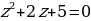 .
.









