Просмотр содержимого документа
«Конспект урока "Четыре замечательные точки треугольника"»
Геометрия, 8 класс
Урок № 54 05.04.2022
Тема урока: Четыре замечательные точки треугольника
Цели урока:
рассмотреть теорему о свойстве биссектрисы угла и ее следствие.
развитие логического мышления, пространственного воображения, математической речи и чувства ответственности за свои знания.
воспитание организованности, культуры и дисциплины труда.
Тип урока: урок применения знаний и умений.
Оборудование: доска, мел, учебник, чертежные принадлежности.
ХОД УРОКА
I. Проверка домашнего задания.
1. № 669 вынести решение на доску.
2. Решить устно:
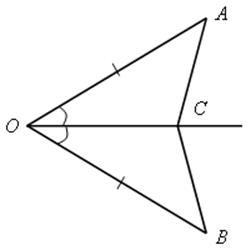
1) Докажите, что SАОС = SВОС.
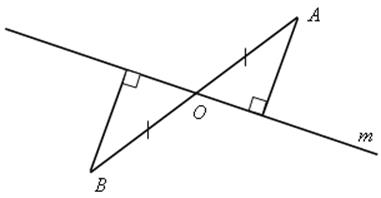
2) Прямая m пересекает отрезок АВ в его середине. Докажите, что концы отрезка АВ равноудалены от прямой m.
II. Изучение нового материала.
1) Доказательство теоремы.
2) Доказательство следствия из теоремы.
Изложить лучше самому учителю в виде небольшой лекции.
III. Закрепление изученного материала.
Решить №№ 674, 675, 676 (а).
№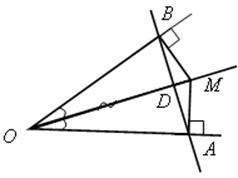 674.
674.
Решение
1)  АОМ =
АОМ = 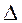 ВОМ (по гипотенузе и острому углу), тогда АО = ОВ.
ВОМ (по гипотенузе и острому углу), тогда АО = ОВ.
2) 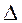 АОВ – равнобедренный, поэтому биссектриса ОD является высотой, то есть DО
АОВ – равнобедренный, поэтому биссектриса ОD является высотой, то есть DО 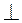 АВ.
АВ.
3) Так как D 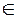 ОМ, то АВ
ОМ, то АВ  ОМ.
ОМ.
№ 675.
675.
Решение
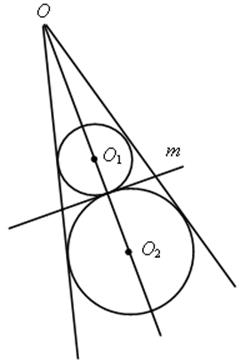
1) Так как отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, то точки О1 и О2лежат на биссектрисе угла (следствие из теоремы п. 69), и, значит, точки О, О1 и О2 лежат на одной прямой.
2) О1А  m и О2А
m и О2А  m (свойство касательной), следовательно, точки А, О1 и О2 лежат на одной прямой. Таким образом, точки А, О, О1, О2 лежат на одной прямой. Тогда точки О1 и О2 лежат на прямой ОА.
m (свойство касательной), следовательно, точки А, О1 и О2 лежат на одной прямой. Таким образом, точки А, О, О1, О2 лежат на одной прямой. Тогда точки О1 и О2 лежат на прямой ОА.
№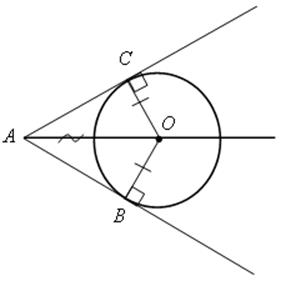 676 (а).
676 (а).
Решение
1) 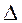 АОВ =
АОВ = 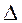 АОС (по гипотенузе и катету), тогда
АОС (по гипотенузе и катету), тогда 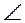 ОАВ =
ОАВ = 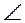 ОАС =
ОАС = 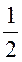
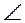 BAC.
BAC.
2) 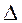 АОВ,
АОВ, 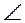 В = 90°
В = 90°
sin 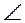 ОАВ =
ОАВ = 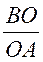 , ВО = ОА · sin
, ВО = ОА · sin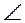 ОАВ = ОА · sin
ОАВ = ОА · sin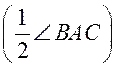 , ОА =
, ОА = 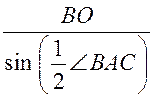 ; ОА =
; ОА = 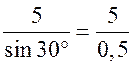 = 10 (см).
= 10 (см).
IV. Итоги урока.
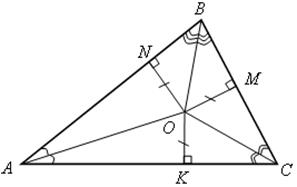
OK = ON = OM.
Домашнее задание: вопросы 15, 16, с. 187; №№ 676 (б), 778 (а).









 674.
674. 675.
675.  676 (а).
676 (а).










