10 класс, алгебра ___________
Урок № 25
Тема: Функция у = хn
Урок усвоения новых знаний
Цель: сформировать понятие степенной функции;
Задачи:
1) Образовательная – рассмотреть свойства степенной функции; формировать умение распознавать графики степенной функции; строить эскизы графиков степенных функций;
2) Развивающая - развивать логическое мышление учащихся через формирование умения строить графики функций.
3) Воспитательная – воспитывать графическую культуру учащихся.
Оборудование: учебник
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Актуализация опорных знаний
Математический диктант
1. Найдите нули функции 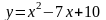 .
.
2. Возрастающей или убывающей является функция 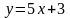 ?
?
3. Найдите промежутки знакопостоянства функции 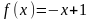 .
.
4. Функция 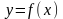 возрастает. Сравните
возрастает. Сравните 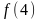 и
и 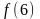 .
.
5. Найдите наибольшее или наименьшее значение функции 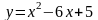 .
.
6. Укажите область определения функции 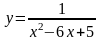 .
.
7. Укажите область изменения функции 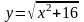 .
.
4. Изучение нового материала.
Определение степенной функции.
Функция вида у = хn, где 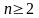 . Область определения функции – множество
. Область определения функции – множество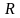 .
.
Функция у = хn для 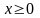 имеет следующие свойства:
имеет следующие свойства:
1. Если 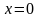 ,то
,то 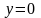 .
.
2. Если 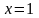 ,то
,то 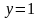 .
.
3. Если 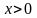 ,то
,то 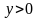 .
.
4. Функция 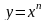 является возрастающей для
является возрастающей для 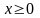 .
.
5. Если 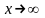 , то
, то 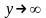 .
.
6. Функция 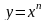 непрерывна.
непрерывна.
Рассмотрим свойства функции 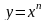 для
для 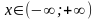 .
.
Для функций с четным показателем:
 ,
,  ,
,  ,
,  ,……,
,……,  .
.
Т.е., при четном  функция
функция 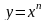 четная и ее график симметричен относительно оси Оу.
четная и ее график симметричен относительно оси Оу.
Для функций вида 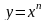 с нечетным показателем выполняются такие равенства:
с нечетным показателем выполняются такие равенства:
 ,
,  ,
,  , ……,
, ……,  .
.
Т.е., при нечетном  функция
функция 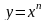 нечетная и ее график симметричен относительно начала координат.
нечетная и ее график симметричен относительно начала координат.
При  - четном, функция является убывающей на промежутке
- четном, функция является убывающей на промежутке  и возрастающей на промежутке
и возрастающей на промежутке  .
.
При  - нечетном, функция является возрастающей на промежутке
- нечетном, функция является возрастающей на промежутке  .
.
5. Решение упражнений
Учебник стр.99-100.
Устно: № №3.11- №3.15.
Письменно: № 3.16(аб), 3.17(аб), 3.18(аб), 3.19(а)
3.17. а) Выясните, какой из графиков двух функций:  или
или  — расположен выше другого на интервале (0; 1).
— расположен выше другого на интервале (0; 1).
Решение. Для любых  из справедливости неравенства
из справедливости неравенства  следует справедливость неравенства
следует справедливость неравенства  , поэтому для любых
, поэтому для любых  график функции
график функции  расположен выше графика функции
расположен выше графика функции  .
.
3.19. а) Выясните, какой из графиков трех функций:  ,
,  ,
,  — расположен выше, а какой ниже других на интервале (−1; 0).
— расположен выше, а какой ниже других на интервале (−1; 0).
Решение. Умножим двойное неравенство  сначала на положительное число
сначала на положительное число  , а потом на положительное число
, а потом на положительное число  , получим два верных двойных неравенства
, получим два верных двойных неравенства  и
и  , из справедливости которых следует, что если
, из справедливости которых следует, что если  , то
, то  . Аналогично показывается, что
. Аналогично показывается, что  . Это означает, что на промежутке (−1; 0) выше других расположен график функции
. Это означает, что на промежутке (−1; 0) выше других расположен график функции  , a ниже других — график функции
, a ниже других — график функции  .
.
6. Итог урока
• Как расположен на координатной плоскости график функции 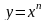 , если
, если  - четное число?
- четное число?  - нечетное число?
- нечетное число?
• Чем отличаются графики функций  и
и  ?
?
7. Домашнее задание:
п.3.2(выучить определение и свойства степенной функции); №№ 3.16(в), 3.17(вг), 3.18(вг).






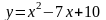 .
.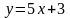 ?
?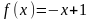 .
.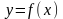 возрастает. Сравните
возрастает. Сравните 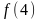 и
и 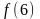 .
.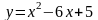 .
.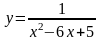 .
.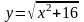 .
.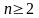 . Область определения функции – множество
. Область определения функции – множество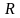 .
.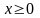 имеет следующие свойства:
имеет следующие свойства: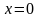 ,то
,то 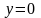 .
.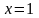 ,то
,то 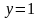 .
.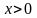 ,то
,то 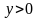 .
.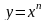 является возрастающей для
является возрастающей для 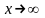 , то
, то 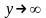 .
.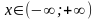 .
.









