Урок геометрии 9 класс
Тема урока: Конус
Цели урока:
-
познакомить учащихся с понятием конуса, его элементами;
-
вывести формулу, выражающую объем конуса и формулу площади боковой поверхности конуса;
-
учить решать задачи;
-
способствовать развитию логического мышления учащихся.
Основные понятия: «конус», «вершина конуса», «боковая поверхность», «основание».
Методы работы:
-
частично-поисковые
-
словесные
-
наглядные
-
практические
Оборудование: компьютер, проектор, раздаточный материал, презентация.
Ход урока
-
Организационный момент
У: Добрый день, ребята! Садитесь!
Сегодня к нам на урок пришли гости, они эксперты в различных отраслях.
- Эксперт в области исторических наук (Ф.И ребенка)
- Эксперт в области архитектуры (Ф.И ребенка)
- Эксперт в области математических наук (Ф.И ребенка)
2. Определение темы урока
Наши гости согласились помочь нам в изучении новой темы. А какую тему мы сегодня будем изучать вы узнаете выполнив задание «Пазл». (Задание построено на основе 19 задания ОГЭ. Дети выбирают верные и неверные утверждения.)
https://learningapps.org/watch?v=p2fgdqty224
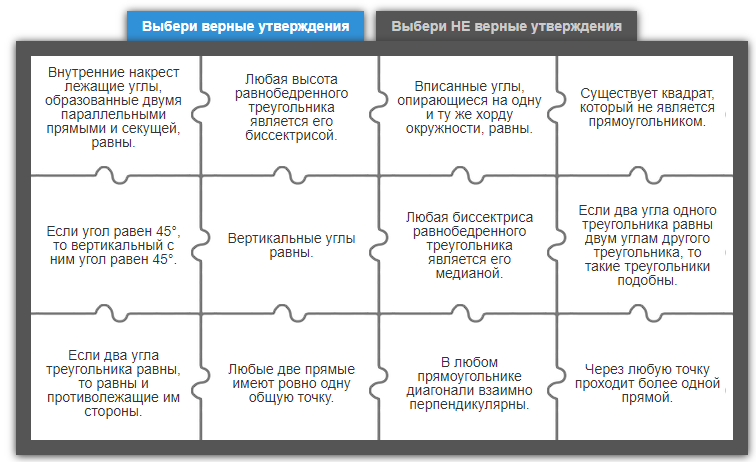

У: Давайте сформулируем цель нашего урока (ответы детей)
3. Историческая справка
Я хочу дать слово эксперту в области исторических наук (Ф.И. ребенка)
Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
У: Ребята вам необходимо сформулировать определение конуса и записать его в тетради для теории. Для этого воспользуйтесь учебниками и раздаточным материалом, который лежат у вас на столе. (Дети работают с учебником и раздаточным материалом. По окончанию работы, ребята читают что у них получилось)
У: Слово предоставляется эксперту в области архитектуры (Ф.И. ребенка). Он расскажет нам о строении конуса.
При построении различных зданий и сооружений очень требуются познания в области геометрии. Очень часто мы встречаем конус в элементах архитектуры. Ярким примером этого наблюдения является конус, который лежит в основании крыш домов. Круглые башни строений покрыты коническими крышами, которые напоминают воронки, перевернутые острым концом вверх.
Конус — это фигура, полученная путём вращения прямоугольного треугольника вокруг одного из его катетов.
Основные элементы конуса:
-
Вершина — верхняя точка фигуры.
-
Основание — круг, который образовался при вращении и оказался в самом низу фигуры.
-
Боковая поверхность — это стенки фигуры, то есть всё, что находится между вершиной и основанием.
-
Образующая — отрезок, проведённый из вершины в любую из точек, лежащих на окружности основания.
-
Высота — перпендикуляр из вершины фигуры в центр её основания.
https://learningapps.org/watch?v=phsxkkqcn24
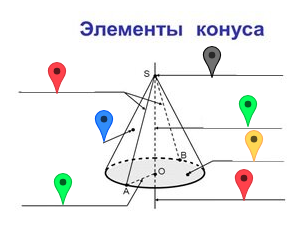
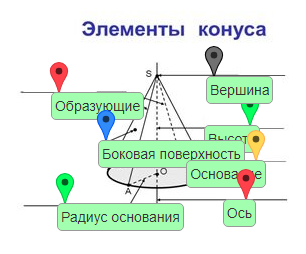
У: У вас на партах лежит карточка с изображением конуса, давайте на ней подпишем все элементы и вклеим в тетрадь для теории.
У: Теперь слово передаем эксперту в области математики (Ф.И. ребенка)
Объём конуса — это объём пространства, заключённого в конус. Обычно он измеряется в кубических метрах, кубических сантиметрах, кубических дюймах и т. д.
Формула для определения объёма конуса равна одной трети произведения площади основания на высоту конуса. Обычно это обозначается буквой «V».

(Дети фиксируют формулы в тетради для формул)
Физкультминутка.
Повторим с помощью ФМ как строятся графики линейной и квадратичной функции.
1.Если график параллелен оси ОХ - разводим руки в стороны;
Проходит через начало координат - руки на пояс; если нет – 1рука вверх, другая - вниз
Ветви параболы идут вверх – руки вверх, вниз – руки вниз.
2. Точка пересечения с осью ОУ: выше 0 – хлопок руками вверху, ниже нуля – внизу, в нуле – руки на пояс.
у = 2х + 3, у = -2х, у = 4, у = х /2, у = - 6х+1, у = -8, у=7х, х =3
у = 2х2 + 3, у = -2х2, , у = х2, у = - 6х2+1, у=7х – х2,
Работа в парах. Учащиеся на листах заполняют таблицу (под копирку).
|
| 1 | 2 | 3 | 4 | 5 |
| l |
|
| 2 | 2 |
|
| r | 1,5 |
|
| 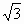
| 3 |
| h | 1,5 |
|
|
|
|
| S |
| 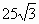
|
|
| 9 |
| a |
| 300 | 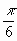
|
|
|
l – образующая конуса, r – радиус его основания, h - высота, S – площадь осевого сечения, a – угол образующей с осью.
Сдают работы. На экран высвечивается заполненная таблица. Учащиеся отмечают на оставшихся листах неправильные ответы.
Подводя итог нашей беседы, мне хочется сказать: «Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
Домашнее задание
п. ___________________________
Ребята, домашнее задание на сегодняшний урок у вас было на УЧИ.РУ. Все отметки будут выставлены в журнал. Мои помощники за урок получают отметку 5. Те кто работал тоже будут оценены.
Рефлексия
https://learningapps.org/view3188524





























