8 класс Геометрия Урок № 34
Тема: Определение подобных треугольников.
Цель: ввести понятие пропорциональных отрезков и подобных треугольников;
рассмотреть свойство биссектрисы треугольника и показать его применение в
процессе решения задач.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга, выявляются отсутствующие.
II. Подготовка учащихся к восприятию нового материала
Фронтальная работа
1) Что называют отношением двух чисел? Что показывает отношение?
2) AB : CD = 2 : 7. О чём это говорит? Найдите отношение CD к AB.
3) В ΔАВС АВ : ВС : АС = 2 : 4 : 3, РАВС = 45 дм. Найдите стороны треугольника АВС.
4) Что называют пропорцией? Верны ли пропорции 1,5 : 1,8 = 25 : 30; 18 : 3 = 5 : 30?
5) В пропорции a : b = c : d укажите крайние и средни члены. Сформулируйте основное свойство пропорции.
6) Переставив средние или крайние члены пропорции, составьте три верные пропорции:
а) 12 : 0,2 = 30 : 0,5;
б) АВ : ОР = КМ : ЕС.
7) Найдите неизвестный член пропорции.
а) 7х : 4,2 = 12,3 : 6;
б) х : АВ = МК : ОР (найти поочерёдно АВ, МК, ОР).
III. Работа по теме урока
1. Ввести понятие отношения отрезков.
Определение: Отношение отрезков АВ и CD называется отношением их длин, т.е.
АВ : CD.
2. Ввести понятие пропорциональных отрезков.
Определение: Отрезки АВ и CD пропорциональны отрезкам А1В1 и C1D1, если 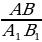 =
= 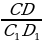 .
.
Например:
Если АВ = 5 см, CD = 7 см, А1В1 = 7,5 см, 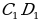 = 10,5 см, то АВ :
= 10,5 см, то АВ : 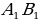 =
= 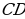 :
: 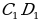 , т.е. отрезки АВ и CD пропорциональны отрезкам
, т.е. отрезки АВ и CD пропорциональны отрезкам 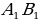 и
и 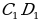 .
.
3. Ввести понятие подобных фигур.
В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любе два квадрата, любые два круга.
4. Ввести понятие подобных треугольников.
ΔАВС  ΔА1В1С1, если ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1,
ΔА1В1С1, если ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1, 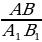 =
= 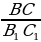 =
= 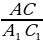 = k, где k – коэффициент подобия.
= k, где k – коэффициент подобия.
Стороны АВ и А1В1, ВС и 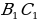 , АС и
, АС и 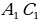 называют сходственными.
называют сходственными.
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
IV. Закрепление изученного материала. Решение задач
1. Работа с задачами из доп. литературы:
Два ученика решает задачи возле доски, а остальные в тетради:
1) Даны отрезки АВ = 12 см, СЕ = 8см, НР = 15 см, МК = 30 см, ОТ = 16 см, XZ = 20 см. Найдите среди них пары пропорциональных отрезков.
2) Подобны ли треугольники АВС и ЕМК, в которых ∠А = 98°, ∠В = 44°, ∠К = 38°,
∠Е = 98°, АВ = 12 , АС = 21, ВС = 30, СЕ = 7, МК = 10, ЕМ = 4?
2. Решение задачи № 535
Ученики самостоятельно читают задачу и её решение. Один ученик работает у доски, остальные – в тетрадях.)
Учитель задаёт вопросы, контролирующие глубину усвоения доказательства:
– Почему 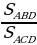 =
= 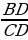 ?
?
– Сформулируйте теорему, на основании которой, если ∠1 = ∠2, то 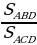 =
=  .
.
– Поясните, на каком основании из равенства 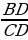 =
= 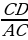 .
.
3. Решение задач № 536 (б) и № 541
Два ученика решают задачи возле доски, остальные – в тетрадях.
Задача № 536
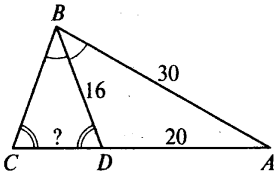 Решение:
Решение:
Так как ∠С = ∠BDС (по рисунку), то ΔBDC -
равнобедренный основанием CD, следовательно,
ВС = BD = 16.
Т.к. BD – биссектриса ΔАBС, то 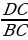 =
= 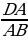 ,
,
следовательно, 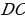 =
= 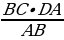 =
= 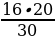 = 10
= 10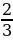 .
.
Ответ: 10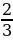 .
.
Наводящие вопросы:
– Как биссектриса треугольника делит противолежащую сторону?
– Длину какого отрезка необходимо найти для нахождения отрезка СD?
– Как можно вычислить длину отрезка ВС?
Задача № 541
Решение:
В ΔАBС ∠А = 106°, ∠В = 34°, следовательно, ∠С = 180° – (∠А + ∠В) = 180° – 140° = 40°.
В ΔDEF ∠Е = 106°, ∠F = 40°, следовательно, ∠D = 180° – (∠E + ∠F) = 180° – 146° = 34°.
По определению подобных треугольников два треугольника называют правильными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
В ΔАBС и ΔDEF ∠А = ∠Е = 106°; ∠В = ∠D = 34°; ∠С = ∠F = 40°;
ВС : DF = 7,6 : 22,8 = 1 : 3; АС : ЕF = 4,4 : 13,2 = 1 : 3; АВ : DE = 5,2 : 15,6 = 1 : 3 
 ΔАBС
ΔАBС  ΔDEF.
ΔDEF.
Наводящие вопросы:
– Когда два треугольника подобны?
– Равны ли углы этих треугольников?
– Пропорциональны ли сходственные стороны данных треугольников?
4. Самостоятельное решение задач
Ученики решают самостоятельно № 534 (в), №537.
№ 534 (в)
Краткое решение:
АВ : ММ1 = 9 : 1; BD : M1M2 = 9 : 2 = 4,5; 9 ≠ 4,5  отрезки АВ и BD не пропорциональны отрезкам ММ1 и M1M2.
отрезки АВ и BD не пропорциональны отрезкам ММ1 и M1M2.
№ 537
Краткое решение:
AD – биссектриса ΔАBС 
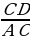 =
= 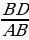

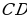 =
= 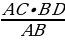 =
= 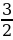 ∙ BD + BD = 20
∙ BD + BD = 20  BD = 8 см
BD = 8 см 
 DС = 20 – 8 = 12 см.
DС = 20 – 8 = 12 см.
Ответ: BD = 8 см, DС = 12 см.
V. Рефлексия учебной деятельности
– Что вы понимаете под «отношением отрезков»?
– Что значит «отрезки АВ и CD пропорциональны отрезкам 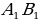 и
и 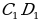 »?
»?
– Приведите примеры подобных фигур.
– Какие треугольники называются подобными?
VI. Анонс домашнего задания
VII. Подведение итогов урока
Учитель выставляет оценки, тем самым подводит итоги урока.







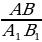 =
= 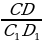 .
.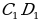 = 10,5 см, то АВ :
= 10,5 см, то АВ : 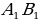 =
= 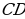 :
:  ΔА1В1С1, если ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1,
ΔА1В1С1, если ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1, 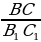 =
= 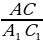 = k, где k – коэффициент подобия.
= k, где k – коэффициент подобия. 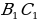 , АС и
, АС и 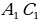 называют сходственными.
называют сходственными.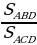 =
= 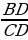 ?
? .
.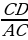 .
. Решение:
Решение: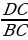 =
= 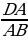 ,
, 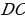 =
= 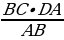 =
= 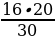 = 10
= 10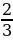 .
.
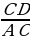 =
= 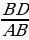
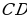 =
= 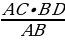 =
= 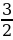 ∙ BD + BD = 20
∙ BD + BD = 20 

















