11 класс Геометрия Урок № 29
Тема: Решение задач на многогранники, цилиндр, конус и шар.
Цели:
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга, выявляются отсутствующие.
II. Проверка домашнего задания
Учитель берёт тетради у 2 – 3 учащихся для проверки домашней работы.
III. Актуализация опорных знаний
Учитель проводит фронтальный опрос:
– Какая призма называется вписанной в сферу?
– Какая призма называется описанной около сферы?
– Какая призма называется правильной?
– Около всякого ли прямоугольника можно описать окружность?
– Где находится центр этой окружности?
– Во всякий ли прямоугольник можно вписать окружность?
– А в какой можно?
IV. Решение задач
1. Теория на комбинацию: призма и шар.
а) Шар вписанный в призму.
– Шар можно вписать в прямую призму, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
– Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центр окружностей вписанных в основания призмы, а радиус шара равен радиусу окружности, вписанной в основание призмы.
б) Шар, описанный около призмы.
– Около призмы можно описать шар тогда, когда призма прямая и около основания можно описать окружность.
– Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведённой через центр окружности, описанной около основания.
2. Решение задач по учебнику
Задача №632
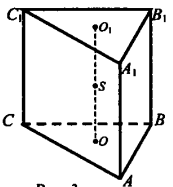 Дано:
Дано:
АВСА1В1С1 – правильная призма,
О и О1 – центры основной призмы;
сфера (S; R) вписанная в призму.
Доказать: OS = SO1.
Доказательство:
Сфера касается всех граней призмы, центр её должен быть равноудалён от оснований, т.е. лежать на середине высоты призмы. Отрезок ОО1, соединяющий центры оснований, является высотой призмы и все точки, лежащие на отрезке ОО1, равноудалены от боковых граней призмы. (О и О1 – центры вписанных в основания окружностей.) Таким образом, середина О1О, точка S, является центром сферы.
Задача №634 (а)
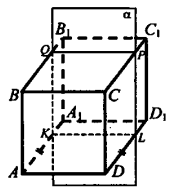 Дано:
Дано:
ABCD А1В1С1D1 – куб, сфера (О; R) вписанная в куб.
Найти: S полной поверхности куба.
Решение:
Рассмотрим сечение KLPQ, где K, L, P, Q – середины
АА1, ВВ1, СС1 и DD1 соответственно. В сечении получим
квадрат и вписанную в него окружность, её радиус равен
радиусу сферы. Пусть ребро куба равно а, а = 2R. Площадь одной грани равна а2 или 4R2.
SП.П. = 6 ∙ 4R2 = 24R2.
Ответ: 24R2.
З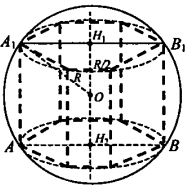 адача №639 (б)
адача №639 (б)
Дано:
Вписанная правильная шестиугольная призма,
Н1Н2 = R высота призмы; сфера (O; R)
Найти: S полной поверхности призмы.
Решение:
Н1 и Н2 – центр оснований призмы.
Рассмотрим сечение призмы плоскостью, проходящей через диаметр оснований призмы перпендикулярного основаниям призмы. Получим прямоугольник АА1В1В.
Из прямоугольного ΔОА1Н1:
А1Н1 = =
= 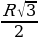 (по теореме Пифагора). А1Н1 – радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности.
(по теореме Пифагора). А1Н1 – радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности.
Сторона основания а. а = 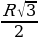 , площадь грани R ∙ а =
, площадь грани R ∙ а = 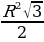 .
.
Sбок. = 6 ∙ 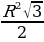 = 3
= 3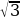 R2.
R2.
Sоcн. = 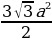 =
=  ∙
∙ 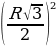 =
=  =
= 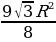 .
.
Sп.п. = 2Sоcн. + Sбок.
Sп.п. = 2 ∙ 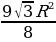 + 3
+ 3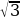 R2 =
R2 =  +
+ 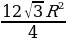 =
=  .
.
Ответ:  .
.
V. Закрепление изученного материала
Самостоятельное решение упражнения
Учащиеся самостоятельно (до конца урока) решают №630.
VI. Подведение итогов урока
Учитель берёт тетради у более подготовленных учеников и проверяет решение №630.
Учитель выставляет оценки,тем самым подводит итоги урок.







 Дано:
Дано: Дано:
Дано: адача №639 (б)
адача №639 (б) =
= 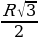 (по теореме Пифагора). А1Н1 – радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности.
(по теореме Пифагора). А1Н1 – радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности. 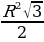 .
. 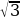 R2.
R2.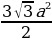 =
=  ∙
∙ 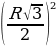 =
=  =
= 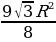 .
. +
+ 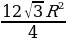 =
=  .
.

















