Конспект урока математики в 6 класса по теме "Параллельные прямые"

Деятельность учителя

Деятельность ученика

УУД

1.Организационный момент

Учитель приветствует учеников. Проверяет готовность к уроку.

Приветствуют учителя. Готовятся к уроку, настраиваются на продуктивную работу.

Коммуникативные:

планирование учебного сотрудничества с учителем и сверстниками.

Регулятивные:

организация своей учебной деятельности.

Личностные: мотивация учения.

2. Сообщение темы урока и постановка цели урока.

Откройте тетради. Запишите число и тему урока «Параллельные прямые»

Мы с вами будем продолжать рассматривать различные линии и познакомимся с новым видом линий - параллельными. Какую цель каждый из вас поставит перед собой на этом уроке?

Записывают число и тему урока.

Формулируют цели урока.

Коммуникативные:

планирование учебного сотрудничества с учителем и сверстниками.

Регулятивные:

организация своей учебной деятельности.

Личностные: мотивация учения.

3.Актуализация знаний и мотивация изучения новой темы

Для того, чтобы хорошо усвоить новый, интересный материал, нам необходимо вспомнить то, что мы уже знаем.

Какую тему мы изучили на прошлом уроке?

Обратите внимание на экран и ответьте на вопросы:

– Какие прямые называются перпендикулярными?

– Какие отрезки и какие лучи называют перпендикулярными?

– С помощью каких инструментов можно построить перпендикулярные прямые?

– Выпишите все пары перпендикулярных прямых (на слайде изображен прямоугольник).

(На первые три вопроса ученики отвечают устно, ответ на четвертый вопрос записывают в тетради, далее идёт обсуждение.)

Посмотрите на слайд.

На какие две группы можно разбить эти прямые?

– Какие пары прямых отнесем к пересекающимся, а какие - не пересекаются?

– Как вы думаете, пересекутся ли прямые под буквой А, если их продолжить дальше?

На прошлых уроках мы рассмотрели пересекающиеся прямые (а именно перпендикулярные). Значит, нам осталось рассмотреть случай, когда прямые не пересекаются.

Посмотрите на слайд и подумайте: если прямые пересекаются, то сколько общих точек у них будет?

А если прямые не пересекаются, сколько у них общих точек?

Перпендикулярные прямые.

Отвечают на вопросы учителя.

Выполняют задание, участвуют в обсуждении, исправляют ошибки.

Пересекающиеся и непересекающиеся.

Отвечают на вопросы.

Коммуникативные:

умение точно выражать свои мысли в соответствии с задачами коммуникации.

Познавательные:

осуществлять анализ объектов с выделением существенных признаков; выбор оснований для сравнения.

Регулятивные:

оценка, выделение и осознание учащимися того, что уже усвоено и того, что еще нужно усвоить, планирование своих действий в соответствии с поставленной задачей.

Личностные:

первичная сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками.

4.Изучение нового материала и первичное закрепление

Так вот, две непересекающиеся прямые на плоскости называют параллельными прямыми.

Название параллельных прямых произошло от греческого слова «параллела», что значит «идущие рядом». Для обозначения параллельных прямых древнегреческие математики использовали знак «=», однако, в 18 веке этот знак начали использовать для обозначения равенства чисел или выражений. А параллельные прямые начали обозначать «||».

Приведите примеры параллельных прямых в окружающей обстановке.

Итак, мы дали определение параллельным прямым, теперь нужно научиться их проводить и обозначать.

(Учимся строить параллельные прямые с помощью линейки и чертежного треугольника)

Задание 1: постройте в тетради параллельные прямые АВ и МК горизонтально, m и n вертикально.

Запишите, что прямые параллельны.

Задание 2: усложним задачу. Дана прямая АВ и точка С, которая не лежит на прямой. Проведите через точку С прямую СD параллельно АВ.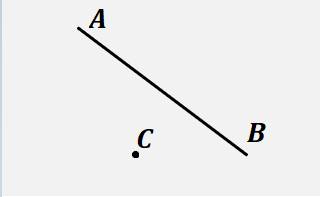

Построение: чтобы построить прямую CD параллельную АВ:

1) приложим угольник к прямой АВ,

2) к другой стороне линейку

3) затем, передвигая угольник вдоль линейки, добьемся того, чтобы точка С оказалась на стороне угольника,

4) проведем прямую СD.

– А сколько таких прямых (параллельных данной) мы сможем провести?

Да, действительно, через точку, не лежащую на прямой, мы можем провести параллельную прямую и притом только одну.

Задание 3:Используя разлиновку тетради,проведите перпендикулярные прямые, обозначьте их. Затем проведите еще одну перпендикулярную прямую к одной из них и обозначьте ее. Сделайте вывод.

Поэтому противоположные стороны любого прямоугольника параллельны. Они образуют прямые углы с двумя другими сторонами этого прямоугольника.

Задание 4: Начертите две пары параллельных прямых. На первых двух прямых отметьте по две точки на кажной. На вторых-по одной.

– Какие геометрические фигуры получились?

– Что можно сказать об этих отрезках и лучах?

– Почему?

Сформулируйте определение параллельных отрезков (лучей).

Нам осталось научиться определять параллельные прямые. Для этого обратимся к учебнику. Выполним №484. Задание:Найдите с помощью линейки и треугольника все пары параллельных прямых, изображенных на рисунке.

Письменно выполним №482,483,485.

Слушают учителя.

Приводят примеры, где в повседневной жизни человек сталкивается с параллельными прямыми.

Выполняют задания совместно с учителем. Учитель показывает, как выполняется построение, на доске, ученики повторяют работу у себя в тетрадях.

Один ученик выходит к доске.

Варианты учеников.

Выполняют задание.

Одну.

Формулируют вывод: Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

Выполняют задание.

Отрезки и лучи.

Они параллельны.

Потому что лежат на параллельных прямых.

Формулируют определение.

Сначала выполняют самостоятельно ,затем, совместно выполняют проверку.

Выполняют задание вместе с учителем.

Личностные:

креативность мышления, инициативы, находчивости, активность при выполнении заданий, формирование аккуратности и терпеливости.

Познавательные:

выдвижение гипотез и их обоснование; формирование умения обобщать, составлять алгоритм математических действий; синтез – составление целого из частей.

Коммуникативные:

осуществление взаимного контроля; умение точно выражать свои мысли в соответствии с задачами коммуникации; инициативное сотрудничество в группе.

5. Домашнее задание

Откройте дневники и запишите домашнее задание.

Дома: Устно: П.44 стр.111-113 (читать, выучить правила).

Письменно: №496, №497.

Дополнительно: №498.

(Комментарии к домашнему заданию).

Записывают домашнее задание.

Регулятивные: планирование своих действий в соответствии с поставленной задачей; Личностные: формирование аккуратности и терпеливости.

6. Подведение итогов и рефлексия

Итак, наш урок подходит к концу.

Как вы считаете- мы достигли поставленной в начале урока цели?

Я предлагаю вам продолжить одно из трёх предложений:

1.Сегодня на уроке я научился(лась) ……

2.У меня лучше всего получалось …..

3.У меня вызвало затруднение …..

Ребята, все молодцы! Хорошо поработали на уроке. Спасибо за урок. До свидания.

Отвечают на вопросы.

Коммуникативные: умение точно выражать свои мысли в соответствии с задачами коммуникации.