Конспект урока по геометрии.
Тема: «Параллельные плоскости. Свойства параллельных плоскостей»
Цели урока:
Образовательные: повторить формулировку утверждений о параллельных плоскостях, доказательство признака параллельности плоскостей; рассмотреть задачи на параллельность плоскостей.
Развивающие: развитие у учащихся памяти, внимания, математического мышления, наблюдательности;
Воспитательные: воспитание математической культуры учащихся, внимательности, аккуратности, дисциплинированности, усидчивости.
Задачи урока:
Закрепить понятие параллельности плоскостей.
Закрепить доказательство признака параллельности плоскостей.
Закрепить свойства параллельности плоскостей.
Рассмотреть задачи на параллельность плоскостей.
Класс: 10.
Тип урока: урок обобщения и систематизации знаний.
Методы обучения: индуктивно-репродуктивный, эвристическое общение.
Требования к знаниям и умениям учащихся:
Знание определения параллельности плоскостей.
Знание признака параллельности двух плоскостей с доказательством.
Знание свойств параллельности двух плоскостей.
Умение решать простые задачи на параллельность плоскостей.
Литература: 1. Геометрия , 10-11: Учеб. Для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.-10-е изд.-М.: Просвещение, 2001.-206 с.: ил.- ISBN 5-09-010749-1.
План урока:
Организационный момент (2 мин.)
Актуализация знаний. Проверка домашнего задания. (17 мин.)
Решение задач (21 мин.)
Подведение итогов урока (3 мин.)
Домашнее задание (2 мин.)
Ход урока:
Организационный момент. Организационный момент включает в себя приветствие учителем класса, проверка отсутствующих и готовность помещения к уроку.
Актуализация знаний. Проверка домашнего задания.
Учитель: На прошлом уроке мы начали изучать тему «Параллельные плоскости. Свойства параллельных плоскостей» Сейчас один из вас должен выйти доске и написать доказательство признака параллельности двух плоскостей.
(Ученик делает чертеж и записывает на доске признак параллельности плоскостей с доказательством)
Ученик: Теорема: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Чертеж на доске:
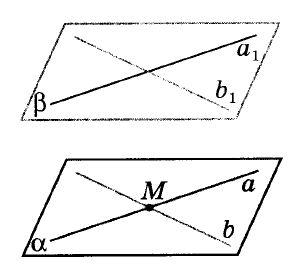
Ученик: Доказательство: рассмотрим две плоскости 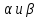 . В плоскости
. В плоскости 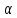 лежат пересекающиеся в точке М прямые a и b, а в плоскости
лежат пересекающиеся в точке М прямые a и b, а в плоскости 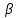 – прямые a1 и b1 , причем
– прямые a1 и b1 , причем 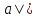 a1, b||b1. Докажем, что
a1, b||b1. Докажем, что 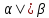 . Прежде всего отметим, что по признаку параллельности прямой и плоскости a||
. Прежде всего отметим, что по признаку параллельности прямой и плоскости a||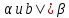 . Допустим, что плоскости
. Допустим, что плоскости 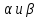 не параллельны. Тогда они пересекаются по некоторой прямой c. Мы получили, что плоскость
не параллельны. Тогда они пересекаются по некоторой прямой c. Мы получили, что плоскость 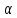 проходит через прямую a, параллельную плоскости
проходит через прямую a, параллельную плоскости 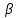 , и пересекает плоскость
, и пересекает плоскость 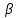 по прямой с. Отсюда следует, что прямые a и c параллельны. Но плоскость
по прямой с. Отсюда следует, что прямые a и c параллельны. Но плоскость 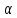 проходит также через прямую b||
проходит также через прямую b|| 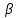 . Поэтому b||c. Таким образом через точку М проходят две прямые a и b ||c. Но это невозможно, так как по теореме о параллельных прямых через точку М проходит только одна, прямая параллельная прямой с. Значит наше предположение неверно и, следовательно,
. Поэтому b||c. Таким образом через точку М проходят две прямые a и b ||c. Но это невозможно, так как по теореме о параллельных прямых через точку М проходит только одна, прямая параллельная прямой с. Значит наше предположение неверно и, следовательно, 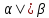 . ч.т.д.
. ч.т.д.
(Пока ученик приводит доказательство признака параллельности двух плоскостей, учитель вызывает двух учеников к доске, показать решение домашнего задания. С остальными проводит фронтальный опрос.)
Учитель: Кто мне сможет сформулировать определение параллельных плоскостей?
Ученик: Две плоскости называются параллельными, если они не пересекаются.
Учитель: Хорошо, садись. Итак, используя чертеж на доске, сформулируйте 1 свойство параллельности плоскостей.
Чертеж на доске:
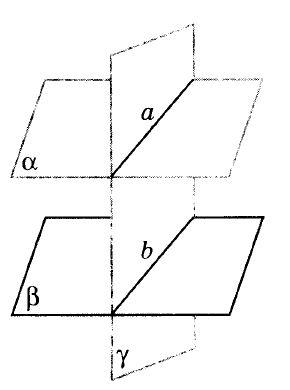
Ученик: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Учитель: Молодец, правильно, садись. Используя следующий чертеж, сформулируйте 2 свойство параллельности плоскостей.
Чертеж на доске:
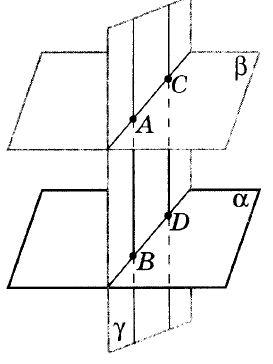
Ученик: Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Учитель: Правильно, садись.
(Затем учитель заслушиваются ответ учащихся, которые готовились у доски.)
Решение задач.
Учитель: Сейчас мы с вами будем решать задания по этой теме. Откройте тетради запишите число, классная работа и тему урока: решение задач.
Запись на доске и в тетрадях: 23.11.10 Классная работа
Решение задач
Учитель: Откройте учебник на странице 23. Задание №63 (б).
(Учитель вызывает одного ученика к доске. А остальных выполняют в тетрадях).
Учитель: прочитай условие задачи
Ученик: Параллельные плоскости 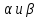 пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла - соответственно в точках В1 и В2. Найдите А2В2 и АА2, если А1В1=18 см, АА1=24 см, АА2 =
пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла - соответственно в точках В1 и В2. Найдите А2В2 и АА2, если А1В1=18 см, АА1=24 см, АА2 =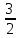 А1А2.
А1А2.
Учитель: итак, с чего начнем решение
Ученик: сначала выполним чертеж
Чертеж на доске:
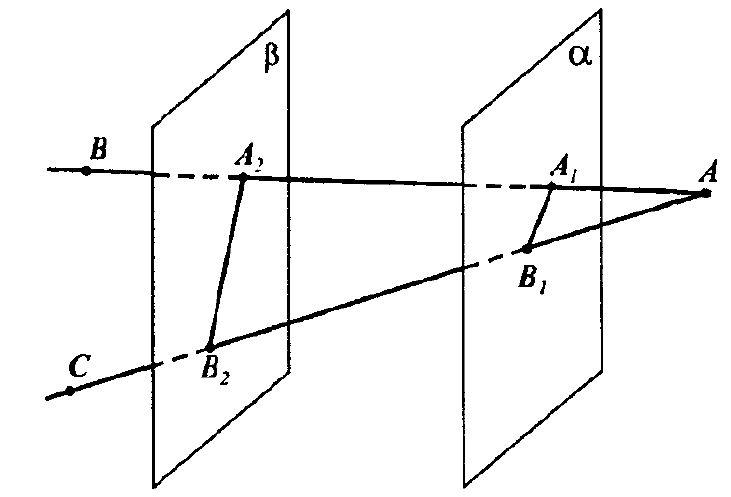
Учитель: давай запиши что нам дано и что нужно найти
Запись на доске: Дано: угол ВАС, 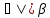 ,
, 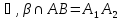 ,
, 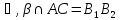 ,
,
А1В1=18 см, АА1=24 см, АА2 =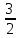 А1А2
А1А2
Найти: А2В2 и АА2
Ученик:
Так как 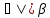 , плоскость (ВАС)
, плоскость (ВАС)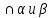 , то А1В1 || А2В2
, то А1В1 || А2В2
Учитель: Почему А1В1 || А2В2
Ученик: по свойству 1
 по первому признаку подобия (угол 1 = углу 3 и угол 2 = углу 4 как соответственные при пересечении двух параллельных прямых А1В1 и А2В2 секущими АВ и АС)
по первому признаку подобия (угол 1 = углу 3 и угол 2 = углу 4 как соответственные при пересечении двух параллельных прямых А1В1 и А2В2 секущими АВ и АС)
Значит 
Учитель: хорошо, что дальше будем делать?
Ученик: Найдем коэффициент подобия
Учитель: тогда чему будет равно АА2
Ученик: Тогда АА2=48+24=72 (см)
Учитель: Следовательно, А2В2=18*3=54 (см)
Ученик: А2В2= 18*3=54 (см)
Ответ: А2В2=54 см, 
Запись на доске и в тетрадях: 1)Так как 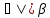 , плоскость (ВАС)
, плоскость (ВАС)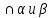 , то А1В1 || А2В2( по свойству 1)
, то А1В1 || А2В2( по свойству 1)
 по первому признаку подобия (угол 1 = углу 3 и угол 2 = углу 4 как соответственные при пересечении двух параллельных прямых А1В1 и А2В2 секущими АВ и АС)
по первому признаку подобия (угол 1 = углу 3 и угол 2 = углу 4 как соответственные при пересечении двух параллельных прямых А1В1 и А2В2 секущими АВ и АС)
Значит 
2) Найдем коэффициент подобия
Тогда АА2=48+24=72 (см)
Следовательно, А2В2=18*3=54 (см)
Ответ: А2В2=54 см, 
Учитель: Молодец. Садись. Теперь давайте приступим к решению задания под номером 65.
(Учитель вызывает одного ученика к доске. А остальных просит этот же номер сделать в тетрадях.)
(Ученик проговаривает условие задачи, записывает на доске чертеж и решение)
Ученик: Параллельные отрезки А1А2, В1В2 и С1С2 заключены между параллельными плоскостями 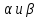
А) Определите вид четырехугольников
Б) Докажите, что
Учитель: выполним чертеж
Чертеж на доске:
Учитель: так как А1А2 и В1В2 – это отрезки параллельных прямых, заключенных между параллельными плоскостями, то по свойству 2?
Ученик: они будут равны
Учитель: Значит в четырехугольнике А1В1В2А2 стороны А1А2 и В1В2
Ученик: равны и параллельны, значит это параллелограмм (по признаку параллелограмма). Аналогично В1С1С2В2 и А1С1С2А2 – параллелограммы.
Учитель: Из того, что вышеперечисленные четырехугольники являются параллелограммами, то что получим ?
Ученик:
Запись на доске и в тетрадях:
Дано: А1А2, В1В2 и С1С2 параллельные отрезки заключены между параллельными плоскостями 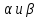
Найти: А) Определите вид четырехугольников
Б) Докажите, что Решение: Так как А1А2 и В1В2 – это отрезки параллельных прямых, заключенных между параллельными плоскостями, то по свойству 2 они будут равны.
Значит в четырехугольнике А1В1В2А2 стороны А1А2 и В1В2 равны и параллельны, значит это параллелограмм (по признаку параллелограмма). Аналогично В1С1С2В2 и А1С1С2А2 – параллелограммы.
Следовательно,
Учитель: Молодец. Садись.
Подведение итогов урока.
Учитель: Итак, мы с вами сегодня закончили изучать тему «Параллельные плоскости. Свойства параллельных плоскостей» Кто сможет мне сейчас сказать свойства параллельности двух плоскостей?
Ученик:1.Две плоскости называются параллельными, если они не пересекаются.
2.Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Учитель: Молодец. А кто может скажет признак параллельности двух плоскостей?
Ученик: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Учитель: Правильно. Садись.
Домашнее задание.
Учитель: урока подходит к концу. Всем тем, кто сегодня отвечал у доски и на мои вопросы устно, я поставлю соответствующие оценки. Откройте дневники, запишите домашнее задание. На дом у вас будет №60, 64 и подготовить ответы на вопросы к главе I (до 14вопроса). Всем спасибо за урок. До свидания.
3








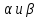 . В плоскости
. В плоскости 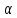 лежат пересекающиеся в точке М прямые a и b, а в плоскости
лежат пересекающиеся в точке М прямые a и b, а в плоскости 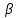 – прямые a1 и b1 , причем
– прямые a1 и b1 , причем 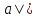 a1, b||b1. Докажем, что
a1, b||b1. Докажем, что 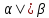 . Прежде всего отметим, что по признаку параллельности прямой и плоскости a||
. Прежде всего отметим, что по признаку параллельности прямой и плоскости a||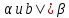 . Допустим, что плоскости
. Допустим, что плоскости 

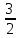 А1А2.
А1А2.
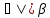 ,
, 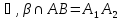 ,
, 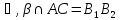 ,
, 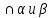 , то А1В1 || А2В2
, то А1В1 || А2В2









