Геометрия
9 класс
Урок № ____
Тема: Параллельный перенос
Цели урока:
Образовательные: формирование понятия параллельного переноса и изучение свойств параллельного переноса; формирование умений учащихся применять изученные определения и свойства к решению задач.
Развивающие: развивать логическое мышление, память, внимание, культуру математической речи.
Воспитательные: воспитывать аккуратность и самостоятельность.
Тип урока: формирование новых знаний.
Ход урока
1. Организационный момент
2. Проверка д/з
3. Формулирование целей и задач урока
4. Актуализация опорных знаний
1. Дайте определение симметрии относительно точки.
2. Какие фигуры являются центрально – симметричными?
3. Дайте определение симметрии относительно прямой.
4. Какие фигуры называются симметричными относительно оси?
5. Изучение нового материала
1. Понятие параллельного переноса
Параллельный перенос — преобразование, при котором точки смещаются в том же направлении на то же расстояние (рис. 169).
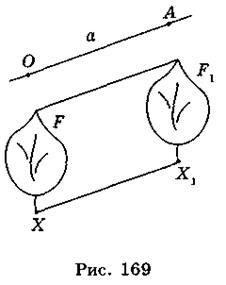
Другими словами, параллельным переносом фигуры F в направлении луча ОА на расстояние а называется преобразование F в фигуру F1, вследствие которого каждая точка X фигуры F переходит в точку Xфигуры 1 F1 в направлении луча ОА на расстояние а.
Введем на плоскости декартовы координаты х и у. Преобразование фигуры F, при котором произвольная точка (х; у) переходит в точку (x + a; y + b), где а, b — те же числа для всех точек (х; у), называется параллельным переносом (рис. 170).
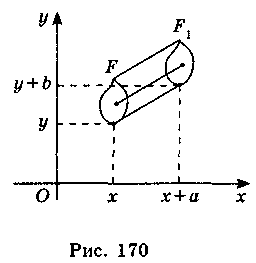
Параллельный перенос задается формулами 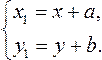 Эти формулы выражают координаты х1, у1 точки фигуры F1, в которую переходит точка (х; у) фигуры F при параллельном переносе.
Эти формулы выражают координаты х1, у1 точки фигуры F1, в которую переходит точка (х; у) фигуры F при параллельном переносе.
2. Свойства параллельного переноса
1) Параллельный перенос является движением.
2) При параллельном переносе точки перемещаются вдоль параллельных прямых (или одной прямой) на то же расстояние.
3) Прямая переходит в параллельную прямую (или в себя); луч переходит в сонаправленный луч.
Два луча называются сонаправленными, если данные лучи параллельны и лежат по одну сторону от прямой, проходящей через их начала, или лучи лежат на одной прямой и один из них является частью второго. На рис. 171 лучи ОА и ВС, ОА и МА, ВС и МА — сонаправленные.
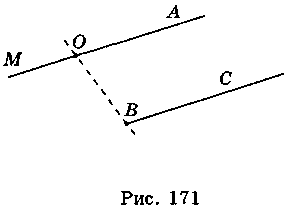
4) Каковы бы ни были точки А и А1, существует единственный параллельный перенос, при котором точка А переходит в точку А.
5) Если точка А1(х1; ух) является образом точки А(х; у) при параллельном переносе, то 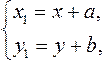 где а, b — некоторые числа.
где а, b — некоторые числа.
6. Закрепление изученного материала
_________________________________________________________________________________________________________________________________
7. Домашнее задание
_______________________________________________________________
8. Подведение итогов урока
Задачи по теме «Параллельный перенос»
1. Параллельный перенос задается формулами х1 = х + 3, y1 = y – 3. В какую точку при этом параллельном переносе переходит точка А(2; 3)?
2. Параллельный перенос задается формулами х1 = х + 1, у1 = - у + 2. Точка А при этом переходит в точку В(2; 3). Найдите координаты точки А.
3. Точка А(1; 2) при параллельном переносе переходит в точку В(3;2). Запишите формулы этого параллельного переноса.
4. Постройте параллелограмм ABCD. Выполните его параллельный перенос:
а) в направлении АВ на расстояние АС;
б) в направлении АС на расстояние АС.
5. Существует ли параллельный перенос, при котором точка А(1; 3) переходит в точку В(0; 2), а точка D(2; 2) переходит в точку С(1; 1)?
6. В результате параллельного переноса точка А(-3; 1) переходит в точку
В(3; -2). В какую точку при таком переносе переходит начало координат?
7. Параллельный перенос задан формулами х1 = х – 2, у1 = у + 2. Запишите уравнения:
а) окружности, в которую переходит окружность
(x – 1)2 + (y – 1)2 = 4;
б) прямой, в которую переходит прямая х + у = 1.







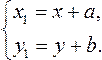 Эти формулы выражают координаты х1, у1 точки фигуры F1, в которую переходит точка (х; у) фигуры F при параллельном переносе.
Эти формулы выражают координаты х1, у1 точки фигуры F1, в которую переходит точка (х; у) фигуры F при параллельном переносе.
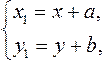 где а, b — некоторые числа.
где а, b — некоторые числа.

















