Конспект урока по геометрии в 9 классе по теме: «Параллельный перенос»

Деятельность учителя

Деятельность учеников

–Еще одним примером движения является параллельный перенос. Определим его.

Опр. Пусть дан вектор . Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка , отображается в такую точку , что вектор равен вектору .

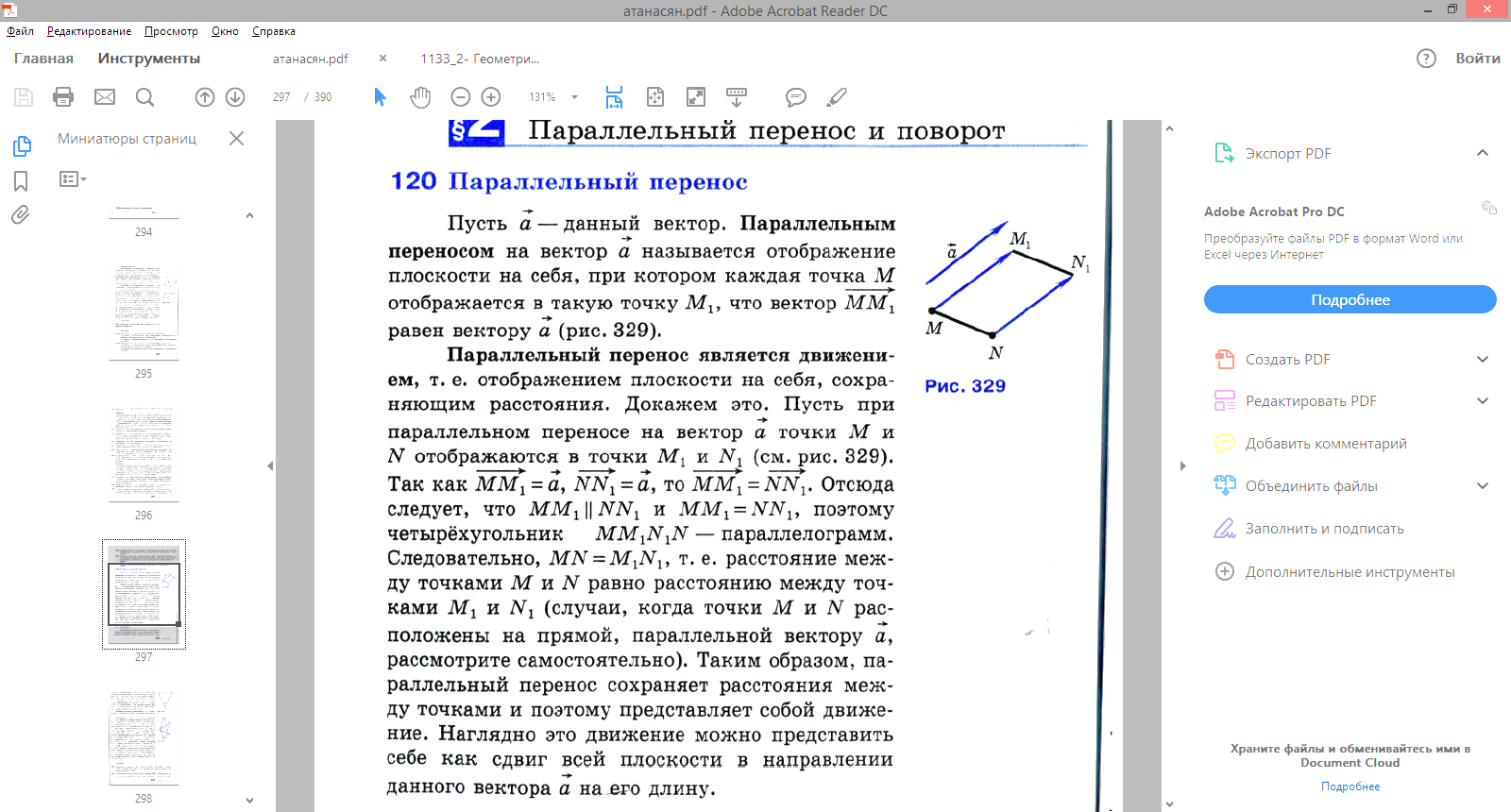
–Как вы думаете, что нужно знать, чтобы выполнить параллельный перенос?

–Верно. Теперь попробуем выполнить параллельный перенос на примере.

Пример. Осуществить параллельный перенос треугольника на вектор

–Что необходимо для начала сделать?

–Действительно, начертим этот треугольник и зададим произвольный вектор. Что нужно сделать дальше?

–Верно, а получившиеся точки, т.е. вершины искомого треугольника обозначим Что еще нам осталось сделать?

–Какое треугольник будет искомым?

–Как уже было сказано ранее, параллельный перенос является примером движения. Но как объясняется данный факт? Докажем следующее утверждение: параллельный перенос является движением, т.е. отображением плоскости на себя, сохраняющим расстояния.

–Пусть нам даны произвольные точки , а также вектор При параллельном переносе эти точки отобразятся в точки .

–Чему равны векторы и ?

–Что из этого следует?

–Верно, а что тогда следует из определения равенства векторов?

–Какой вывод из этого можно сделать о четырехугольнике ?

–Т.к. четырехугольник – параллелограмм, в каком соотношении находятся его стороны и ?

–Действительно, значит расстояние между точками равно расстоянию между точками (аналогично рассматривается случай, когда точки расположены на прямой, параллельной вектору ).

–Какой же вывод мы можем сделать о параллельном переносе?

–А это означает, что параллельный перенос является движением. Такое движение можно представить как сдвиг плоскости в направлении данного вектора на его длину.

Слушают учителя, отвечают на вопросы, делают записи в тетради.

–Чтобы задать преобразование параллельного переноса, достаточно задать вектор .

–Нам нужно начертить треугольник и задать вектор

–Мы отложим от каждой вершины треугольника вектор

–Осталось соединить найденные вершины.

–Искомым будет треугольник

(Чертеж выполняется совместно с рассуждениями)

Слушают учителя, отвечают на вопросы, делают записи в тетради.

–Согласно определению параллельного переноса векторы и .

–Мы получаем, что .

–Из определения равенства векторов мы получаем: и .

– Четырехугольник является параллелограммом.

–Стороны =.

–Мы получили, что параллельный перенос сохраняет расстояние между точками.

Деятельность учителя

Деятельность учеников

Решаются задания по изученной теме. Упражнения выполняются в тетради и на доске.

№ 1162, № 1164.