Конспект урока по теме: "Средняя линия треугольника" (Геометрия, 8 класс)

8 класс ГЕОМЕТРИЯ Урок № 39

Тема: Средняя линия треугольника

Цели: рассмотреть теорему о средней линии треугольника и свойство медиан
треугольника, показать их применение в процессе решения задач;
совершенствовать навыки решения задач на применение теории подобных
треугольников.

ХОД УРОКА

I. Организационный момент. Мотивация к учебной деятельности

Учитель и ученики приветствуют друг друга. Выявляются отсутствующие. Учитель сообщает тему урока, формулирует цели урока.

II. Анализ ошибок, допущенных в контрольной работе

1. Провести общий анализ контрольной работы.

2. Решить задачи, с которыми не справилось большинство учащихся.

3. Работа над ошибками.

III. Подготовка к восприятию нового материала

П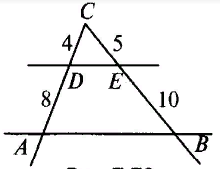 овторение теоритического материала в процессе решения задач по готовым чертежам.

1. Дано:
CD = 4, AD = 8, CE = 5, BE = 10.
Доказать: а) CDЕ CАВ
б) АВ 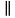DЕ.

2. Дано: ABCD – трапеция
Доказать:
а) ВО : OD = CO : OA;
б) DO : BO = 2, если ВС = .

IV. Работа по теме урока

1. Ввести определение средней линии треугольника

Учащиеся делают запись в тетради:

На доске учитель чертит рисунок и делает запись:

Е сли АМ = МВ и CN = NB,
то MN – средняя линия АВС.

2. Свойства средней линии треугольника (работа в группах).

Учитель делит класс на группы. На обсуждение даётся 2 – 3 минуты. Далее заслушивают представителей групп, в обсуждении участвует весь класс.

3. Теорема о средней линии треугольника с доказательством.
На доске учитель делает рисунок и запись:

4. Решить задачи № 564, 565 (устно).

Рисунки к этим задачам подготовить на доске заранее

№ 564 №565

5. Решение задач.

Решить задачу № 1 стр. 146 (работа в группах).

Указания для решения задачи:

1. Постройте две медианы треугольника и докажите, что точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины.

2. Постройте третью медиану и докажите, что она проходит через точку пересечения первых двух и делится этой точкой в отношении 2 : 1, считая от вершины.
   
   
   
   

Наводящие вопросы:

- Соедините точки А₁ и В отрезком. Что можно сказать о треугольниках АОВ и А₁ОВ₁?

- Почему медианы СС₁ и ВВ₁ также пересекаются в точке О?

- Это свойство называют свойством медиан треугольника, оно широко используется при решении задач.

6 . Решить задачу для закрепления свойства медиан треугольника (устно).

Дано: В треугольнике АВС медианы АА₁, ВВ₁ и СС₁,
равные соответственно 6 см, 9 см и 12 см, пересекаются
в точке О.
Найти: АО + ОВ + СО.

V. Работа учащихся в тетради

Решить задачи № 567, 568.

Учитель контролирует работу менее подготовленных учащихся и по мере необходимости оказывает индивидуальную помощь.

VI. Рефлексия учебной деятельности

1. Что называют средней линией треугольника?

2. Сформулируйте теорему о средней линии треугольника.

3. Средние линии треугольника равны 5 см, 7 см и 8 см. Найдите периметр треугольника.

4. Сформулируйте свойство медиан треугольника.

VII. Домашнее задание

• Прочитать пункт 64

• Решить задачи № 570, 571.

VIII. Подведение итогов урока

Оценивание работы учащихся на уроке