8 класс АЛГЕБРА Урок № __
Тема: Свойства степени с целым показателем.
Тип: урок – изучения нового материала.
Цель: изучить свойства степени с целым показателем и их использование при решении
задач.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга. Выявляются отсутствующие
II. Сообщение темы и цели урока
III. Повторение и закрепление раннее пройденного материала
1. Разбор решения домашней работы
2. Контроль усвоения материала (тест).
Вариант I
1. Представьте в виде дроби выражение 5х2у-3z0.
Варианты ответов: а) 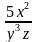 ; б)
; б)  ; в)
; в)  .
.
2. Найдите значение выражения 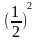 +
+ 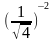 ∙ 2-3.
∙ 2-3.
Варианты ответов: а) 0,75; б) 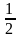 ; в)
; в) 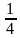 .
.
3. Упростите выражение (у-2 - х-2) : (у – х).
Варианты ответов: а) 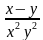 ; б)
; б) 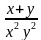 ; в)
; в)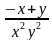 .
.
Ответы на I Вариант: 1 – в); 2 – а); 3 – в).
Вариант II
1. Представьте в виде дроби выражение 6х0у-5z3.
Варианты ответов: а) 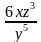 ; б)
; б) 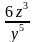 ; в)
; в) 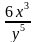 .
.
2. Найдите значение выражения  ∙
∙  + (
+ ( -6.
-6.
Варианты ответов: а) 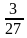 ; б)
; б) 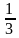 ; в)
; в) 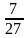 .
.
3. Упростите выражение (a-2 + b-2) : (a2 + b2).
Варианты ответов: а) 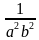 ; б)
; б) 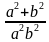 ; в)
; в) 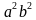 .
.
Ответы на II Вариант: 1 – б); 2 – в); 3 – а).
IV. Изучение нового материала (основные понятия)
- Давайте вспомним свойства степени с натуральным показателем, которые мы изучили в 7 классе.
1) am ∙ an = am+n ; 2) am : an = am – n ; 3) 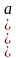 )n = amn ;
)n = amn ;
4) (ab)n = anbn ; 5) 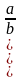 =
=  (при b ≠ 0).
(при b ≠ 0).
А теперь, давайте на примерах проверим, выполняются ли эти свойства в случае отрицательных целых показателей степени (с очевидным ограничением a ≠ 0, b ≠ 0).
Пример 1
а)  =
= 
 =
= 
 =
=  =
=  =
=  =
=  (свойство 1).
(свойство 1).
б) (2 ∙ 3)-2 =  =
=  и
и 

 =
= 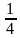
 =
=  , т.е (2 ∙ 3)-2 =
, т.е (2 ∙ 3)-2 =  (свойство 4).
(свойство 4).
- На основании этих примеров можно высказать гипотезу, что свойства 1 – 5 выполняются и в случае степени с целым отрицательным показателем.
- Я предлагаю вам доказать, например, свойства 1 и 4 в случае степени с целым отрицательным показателем.
Пример 2
Докажем свойство 1, то есть am ∙ an = am+n (где т и п – целые отрицательны числа, a – любое число (a≠ 0)).
По определению степени с целым отрицательным показателем запишем am =  и an =
и an =  . Числа (-т) и (-п)являются уже натуральными. Поэтому по свойству степеней с натуральными показателями получаем:
. Числа (-т) и (-п)являются уже натуральными. Поэтому по свойству степеней с натуральными показателями получаем:
am ∙ an =  ∙
∙  =
=  =
=  =
=  = am+n. На заключительном этапе вновь было использовано определение степени с целым отрицательным показателем.
= am+n. На заключительном этапе вновь было использовано определение степени с целым отрицательным показателем.
Пример 3
Докажем свойство 4, то есть (ab)n = anbn (где п – целое отрицательное число, a и b – любые числа (a≠ 0, b≠ 0).
По определению степени с целым отрицательным показателем запишем (ab)n =  . Число (-п) будет уже натуральным. По свойству степеней с натуральными показателями имеем: (ab)n =
. Число (-п) будет уже натуральным. По свойству степеней с натуральными показателями имеем: (ab)n = =
=  =
= = an
= an bn. В конце снова было использовано определение степени с целым отрицательным показателем.
bn. В конце снова было использовано определение степени с целым отрицательным показателем.
Таким, образом, свойства 1 – 5 (для натуральных показателей степени) можно обобщить и на случай целых отрицательных показателей степени.
Пример 4
Преобразуем выражения: а)  ; б)
; б) ; в) (
; в) ( -4 ; г) (
-4 ; г) ( -2.
-2.
а) Учтём, что при умножении чисел с одинаковыми основаниями показатели степеней складываются. Получаем  =
=  =
=  .
.
б) При делении чисел с одинаковыми основаниями показатели степеней вычитаются. Имеем:  =
=  .
.
в) При возведении в степень дроби возводят в эту степень каждый множитель и результаты перемножают. При возведении степени в степень основание оставляют прежним, а показатели перемножают. Получаем: ( -4 = (
-4 = ( -4
-4  (
( -4 =
-4 =  =
=  .
.
г) При возведении в степень дроби возводят в эту степень её числитель и знаменатель и результаты делят. При возведении степени в степень основание оставляют прежним, а показатели перемножают. Имеем: ( -2 = =
-2 = =  =
=  .
.
Упомянутые свойства степеней используются и при решении более сложных задач.
Пример 5
Упростить выражение:
а) ( -2
-2  (
( -2 : (
-2 : ( 2;
2;
б)  .
.
Используем свойства степеней и получим:
а) ( -2
-2  (
( -2 : (
-2 : ( 2 = =
2 = =  =
=  =
=  .
.
б)  =
=  =
=  =
=
 =
=  =
=  =
= .
.
V. Решение упражнений
№ 986; 1079; 989; 990; 992; 993; 999.
VI. Домашнее задание
№ 985; 991; 994.
VII. Оценивание







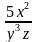 ; б)
; б)  ; в)
; в)  .
.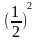 +
+ 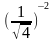 ∙ 2-3.
∙ 2-3.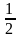 ; в)
; в) 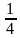 .
.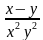 ; б)
; б) 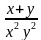 ; в)
; в)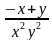 .
.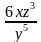 ; б)
; б) 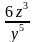 ; в)
; в) 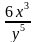 .
. ∙
∙  + (
+ ( -6.
-6.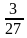 ; б)
; б) 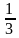 ; в)
; в) 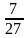 .
.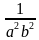 ; б)
; б) 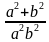 ; в)
; в) 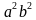 .
.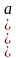 )n = amn ;
)n = amn ;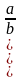 =
=  (при b ≠ 0).
(при b ≠ 0). 


















