Просмотр содержимого документа
«Конспект урока по теме: "Задачи на дроби" (Математика, 5 класс)»
5 класс Математика Урок №103
Тема: Задачи на дроби.
Основные дидактические цели:
1) рассмотреть решение задач, в которых требуется найти часть числа или число по его части;
2) научиться решать задачи на дроби.
ХОД УРОКА
I. Организационный момент. Мотивация к учебной деятельности
Учитель и ученики приветствуют друг друга, выявляются отсутствующие. Учитель читает стихотворение:
Вот книжка на столе,
А вот тетрадка,
Не хочется играть
Сегодня в прятки.
И недосуг дуть
На корабль бумажный -
Сегодня в классе у ребят
Урок уж очень важный.
II. Анализ самостоятельной работы
III. Постановка темы и целей урока
Учитель анонсирует тему и цели урока
IV. Изучение нового материала
- Давайте рассмотрим решение следующих задач:
Задача 1. Было 320 р., 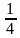 этой суммы истратили. Сколько денег истратили?
этой суммы истратили. Сколько денег истратили?
Решение. Чтобы найти 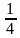 от 320 р., надо эту сумму разделить на 4:
от 320 р., надо эту сумму разделить на 4:
320 : 4 = 80 (р.).
Ответ: 80 р.
Задача 2. Было 1000 р., 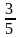 этой суммы истратили. Сколько денег истратили?
этой суммы истратили. Сколько денег истратили?
Решение. Будем считать, что 1000 рублей состоит из пяти пятых долей. Сначала найдём одну пятую от 1000 рублей, а потом три пятых:
1) 1000 : 5 = 200 (р.)
2) 200 3 = 600 (р.)
Ответ: 600 р.
Исходя из этой задачи, справедливо правило:
Учитель диктует ученикам правило:
| Если часть целого выражена дробью, то, чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель. |
Задача 3. Было 100 р., это составило 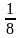 первоначальной суммы денег. Найдите первоначальную сумму денег.
первоначальной суммы денег. Найдите первоначальную сумму денег.
Решение. 100 р. в 8 раз меньше первоначальной суммы, т.е. первоначальная сумма в 8 раз больше, чем 100 р. Чтобы найти эту сумму, надо 100 р. умножить на 8:
100 8 = 800 (р.).
Ответ: 800 р.
Задача 4. Потратили 500 р., это составило 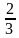 первоначальной суммы денег. Найдите первоначальную сумму денег.
первоначальной суммы денег. Найдите первоначальную сумму денег.
Решение. Будем считать, что искомое число состоит из трёх третьих долей. По условию его две трети равны 500. Сначала найдём одну треть первоначальной суммы, а потом и три третьих:
500 : 2 3 = 750 (р.).
Ответ: 750 р.
Исходя из этой задачи, справедливо правило:
Учитель диктует ученикам правило:
| Если часть искомого целого выражена дробью, то, чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель. |
V. Решение упражнений
Устно: №776
Письменно: № 777, 779 – 780.
VI. Анонсирование домашнего задания
Прочитать п. 4.3
Решить № 778
VII. Подведение итогов урока
Оценивание деятельности учащихся







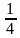 этой суммы истратили. Сколько денег истратили?
этой суммы истратили. Сколько денег истратили? 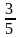 этой суммы истратили. Сколько денег истратили?
этой суммы истратили. Сколько денег истратили? 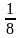 первоначальной суммы денег. Найдите первоначальную сумму денег.
первоначальной суммы денег. Найдите первоначальную сумму денег. 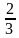 первоначальной суммы денег. Найдите первоначальную сумму денег.
первоначальной суммы денег. Найдите первоначальную сумму денег.









