Тема: Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом и тангенсом одного и того же угла.
Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической.
Длина этой окружности , как мы помним из уроков геометрии, 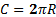 . А учитывая, что R=1,
. А учитывая, что R=1, 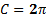 , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
, осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
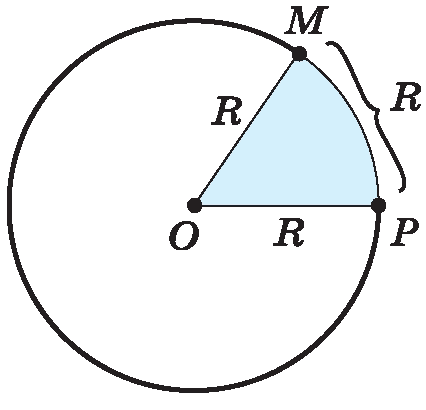
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад. 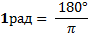 ;
;
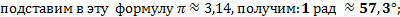
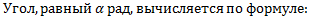 α рад=(180/π α)° (1)
α рад=(180/π α)° (1)
Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1.
Введём понятие поворота точки.
Пусть 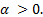 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 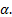
Пусть 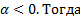 точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол - α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол - α.
При повороте на 0 рад точка остаётся на месте.
Пример 1.
Найти градусную меру угла, равного 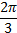 рад.
рад.
Решение: Используя формулу (1), находим 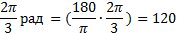 .
.
Так как 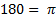 , то
, то 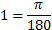 рад, тогда
рад, тогда 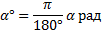 (2)
(2)
Ответ: 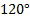 .
.
Пример 2. Найти радианную меру угла, равного 60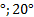 .
.
Решение: Вычисляем по формуле (2): 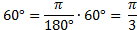 рад
рад
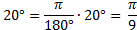 рад
рад
При обозначении мер угла, наименование «рад» опускают.
Ответ:  ,
,  .
.
Как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.
1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической.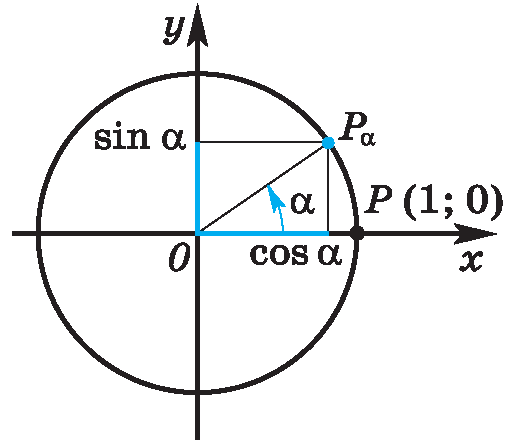 Точка Р на единичной окружности
Точка Р на единичной окружности
Точка Р (1; 0) при повороте вокруг начала координат на угол 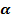 переместилась в точку Рₐ.
переместилась в точку Рₐ.
Синусом угла 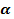 называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол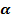 .
.
Обозначается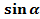
Косинусом угла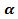 называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол 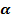 . Обозначается
. Обозначается  . Угол
. Угол 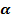 может выражаться и в градусах и в радианах.
может выражаться и в градусах и в радианах.
Пример 1. Точка А(1; 0) при повороте на угол 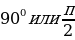 переместилась в точку В(0;1). Ордината точки В равна 1, значит
переместилась в точку В(0;1). Ордината точки В равна 1, значит 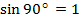 или
или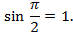 Абсцисса точки В равна 0, значит
Абсцисса точки В равна 0, значит 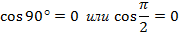
Пример 2. Точка А(1; 0) при повороте на угол 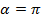 переместилась в точку
переместилась в точку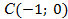 . Найдите
. Найдите 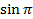 и
и 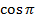
Ответ: 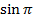 = 0;
= 0; 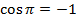
Пример 3. Точка А(1; 0) при повороте на угол 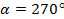 переместилась в точку
переместилась в точку 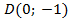 . Найдите
. Найдите 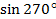 и
и 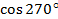 . Ответ:
. Ответ: 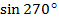 =
=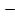 1
1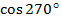 = 0.
= 0.
Определение. Тангенсом угла 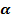 называется отношение синуса угла к его косинусу.
называется отношение синуса угла к его косинусу.
Обозначается tg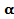 : tg
: tg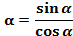 ,
, 
Пример 4. Найти tg 0. Вычислим по формуле tg 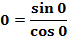 =
= 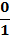 = 0.
= 0.
Определение. Котангенсом угла 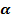 называется отношение косинуса угла к его синусу.
называется отношение косинуса угла к его синусу.
Обозначается сtg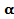 . сtg
. сtg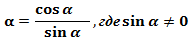
Пример 5. Найти сtg  . Вычислим по формуле сtg
. Вычислим по формуле сtg 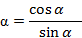 =
= 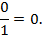
2. Меру угла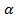 (в радианах) можно рассматривать как действительное число, поэтому
(в радианах) можно рассматривать как действительное число, поэтому 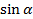 и
и 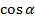 – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1,то синус и косинус не могут превышать значения, больше
– это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1,то синус и косинус не могут превышать значения, больше 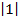 .
.
Какие знаки имеют координаты точки в зависимости от их положения в системе координат?
У точек первой четверти 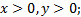 у точек второй четверти
у точек второй четверти 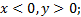
у точек третьей четверти 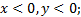 у точек четвёртой четверти
у точек четвёртой четверти 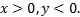
Рассмотрим точку В(х;у), лежащую на тригонометрической окружности . Она получена поворотом точки А(1;0) вокруг начала координат на угол 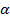 .
.
Синусом угла 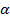 является ордината точки В(х;у). Косинусом угла
является ордината точки В(х;у). Косинусом угла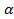 является её абсцисса. Образовался прямоугольный треугольник ОВС.
является её абсцисса. Образовался прямоугольный треугольник ОВС.
По теореме Пифагора 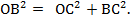 Катет ОС - это абсцисса точки В или
Катет ОС - это абсцисса точки В или 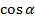 , катет ВС- её ордината, или
, катет ВС- её ордината, или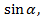 а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу: (1)
(1)
В тригонометрии её называют основным тригонометрическим тождеством. Она связывает синус с косинусом. А это значит, что зная значения синуса, можно найти значения косинуса и наоборот.
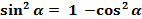
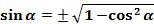 (2)
(2) 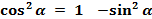
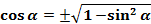 (3)
(3)
В этих равенствах знаки перед корнем определяются по знакам синуса и косинуса.
Пример. Найти 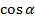 , если
, если 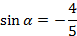 ,
, 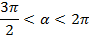 .Выясним знак косинуса. Из условия опрелеляем, что угол
.Выясним знак косинуса. Из условия опрелеляем, что угол 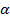 в 4 четверти,
в 4 четверти, 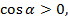 Подставим значение
Подставим значение 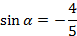 в формулу (3), получаем:
в формулу (3), получаем:
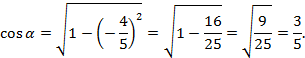 Ответ:
Ответ:  .
.
Пример . Известно, что 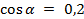 ;
; 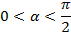 . Найти
. Найти 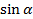 ,
, 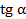 и
и 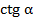 .
.
Угол 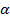 в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
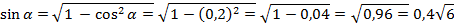 ;
;
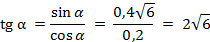 ;
;
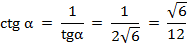 . Применяя тригонометрические формулы, можно зная одно из чисел
. Применяя тригонометрические формулы, можно зная одно из чисел
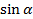 ,
, 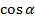 ,
, 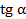 и
и 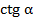 , найти остальные три. Эти формулы являются тождествами.
, найти остальные три. Эти формулы являются тождествами.








 Точка Р на единичной окружности
Точка Р на единичной окружности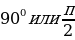 переместилась в точку В(0;1). Ордината точки В равна 1, значит
переместилась в точку В(0;1). Ордината точки В равна 1, значит 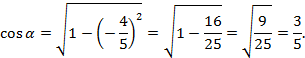 Ответ:
Ответ: 

















