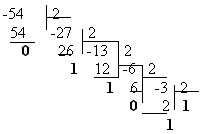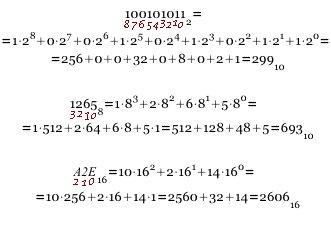Тема урока. Система счисления
Цель урока:
Образовательная:
знакомство с понятием «система счисления»;
умение различать виды систем счисления и применять их на практическом занятии;
умение правильно записывать числа в системах счисления;
формирование способности для применения правил перевода чисел из одной системы счисления в другие.
Развивающая:
развивать логическое мышление, умение обобщать, конкретизировать;
формирование внимания, умения наблюдать и закреплять знания;
Воспитательная:
воспитывать самостоятельность, уважительное отношение друг к друг;
воспитание информационной культуры учащихся.
Этапы урока:
1.Организационный момент.
2. Изучение нового материала.
3. Практическая часть.
4.Подведение итогов.
Ход урока:
1.Организационный момент.
Приветствие, проверка присутствующих.
2. Изучение нового материала.
С древних времен в практической деятельности человека часто возникала потребность счета и измерения. Результаты счета предметов выражались вначале весьма примитивно: зарубки на палочках, узелки на веревках и др. С развитием письменности человек начал отображать с помощью знаков (записывать) информацию о количестве предметов на подручных материалах: глиняных табличках, папирусе, бересте и др. Таким образом, для обозначения чисел стали использовать знаки.
Способ записи чисел с помощью письменных знаков называют системой счисления. Знаки, с помощью которых записываются числа, называют цифрами, а их совокупность — алфавитом системы счисления.
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
Человек использует десятичную систему счисления, а компьютер – двоичную систему счисления. Поэтому часто возникает необходимость перевода чисел из десятичной системы в двоичную и наоборот.
3.3. Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
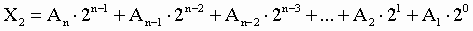
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Пример . Число 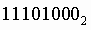 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
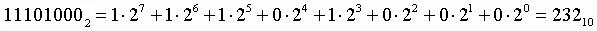
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
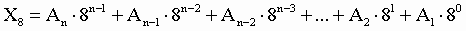
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 
| 1 | 8 | 64 | 512 | 4096 | 32768 | 262144 |
Пример . Число 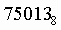 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
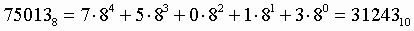
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
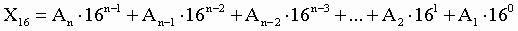
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 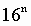
| 1 | 16 | 256 | 4096 | 65536 | 1048576 | 16777216 |
Пример . Число 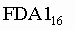 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
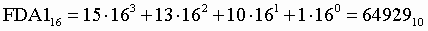
Запишем степени чисел:
Степени двойки :

Степень восьмерки :
80=1
81=8
82=64
83=512
84=4096
Степень шестнадцати :
160=1
161=16
162=256
163=4096
Перевод целых чисел из десятичной системы счисления в двоичную систему счисления
Алгоритм перевода целого десятичного числа в двоичное:
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы счисления ( на 2) до тех пор, пока частное от деления не окажется равным нулю;
Получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.
Например:
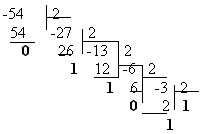
5410=1101102
Перевод десятичных дробей в двоичную систему счисления
Алгоритм перевода десятичной дроби в двоичную:
Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы ( на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений;
Получить искомую двоичную дробь, записав полученные целые части произведений в прямой последовательности.
Например, переведём десятичную дробь 0,7510 в двоичную систему
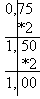
0,7510=0,112
Перевод чисел, содержащих и целую, и дробную часть, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно – дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.
Например, переведём десятичную дробь 71,510 в двоичную систему счисления
Переведём целую часть 7110 в двоичную систему счисления по алгоритму перевода целого десятичного числа в двоичное:
7110=10001112
Переведём дробную часть методом последовательного умножения:
0,510=0,12
Запишем результат 71,510=1000111+ 0,1= 1000111,12
Преобразование из двоичной системы счисления в десятичную осуществляется с помощью выражения вида: Xs=A 0S0+ A 1S1+ A 2S2+…, где Xs – число в S-й системе счисления, S – основание системы, А – цифра числа. Данное выражение используется для преобразования целых чисел, причём отчёт цифр идёт справа налево.
Например, перевести число 1101102 в десятичную систему счисления. 1101102=0*20+1*21+1*22+0*23+1*24+1*25= 0+2+4+0+16+32=5410
Аналогичным образом можно использовать формулу и для отрицательных чисел, и для нахождения дробной части числа.
Например, перевести число 10,112 в десятичную систему счисления.
10,112=1*2-2+ 1*2-1+0*20+1* 21=1/4+1/2+0*1+1*2=0,25+0,5+0+2=2,7510
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
пронумеровать разряды исходного числа;
записать сумму, слагаемые которой получаются как произведения очередной цифры на основание системы счисления, возведенное в степень, равную номеру разряда;
выполнить вычисления и записать полученный результат (указав основание новой системы счисления — 10).
Примеры:
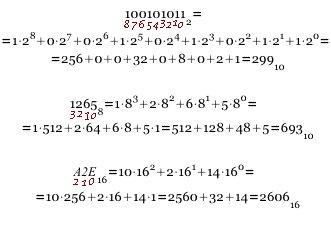
3. Практическая часть.
Перевод чисел из одной системы счисления в другую
4.Подведение итогов.
Досвидание. Спасибо за урок.