Тема урока: Свойства равнобедренного треугольника.
Предмет: геометрия
Класс: 7б класс
Тип урока: урок изучения и первичного закрепления знаний
Используемые учебники и учебные пособия: Л.С. Атанасян и др. Геометрия 7-9.
Используемое оборудование: компьютер, мультимедийный проектор
Планируемые результаты:
Личностные: ответственное отношение к учебе, умение ясно излагать мнение, умение определять правильность, дружелюбное отношение к другим
Метапредметные: умение ставить цель, планировать, выполнять работу по образцу и алгоритму, строить логические заключения, определять удобные (рациональные) способы решения, анализировать, сравнивать, определять важное; умение работать в паре
Предметные: уметь применять свойства равнобедренного треугольника при решении задач.
ХОД УРОКА
I. Организационный момент
II. Повторение основных понятий
На данном этапе урока повторяем изученные ранее понятия: “медиана”, “биссектриса”, “высота” треугольника. Я предлагаю повторить эти понятия, используя тест «Медианы, биссектрисы и высоты треугольника». Повторение ведётся посредством фронтального опроса учащихся. (слайды
Задание 1
Вопрос:
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется ...
Задание 2
Вопрос:
Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или её продолжение, называется ...
Задание 3
Вопрос:
В треугольнике АВС отрезок ВD делит угол АВС на два равных угла. Как называется отрезок ВD?
Изображение:
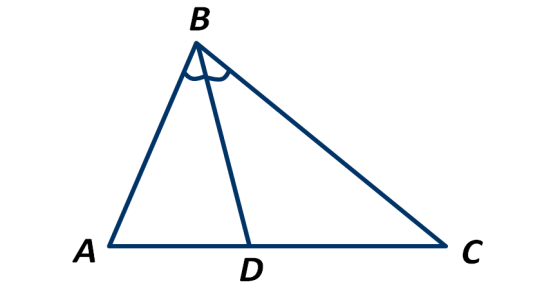
Задание 4
Вопрос:
В треугольнике провели две медианы. Сколько всего треугольников изображено на рисунке?
Изображение:
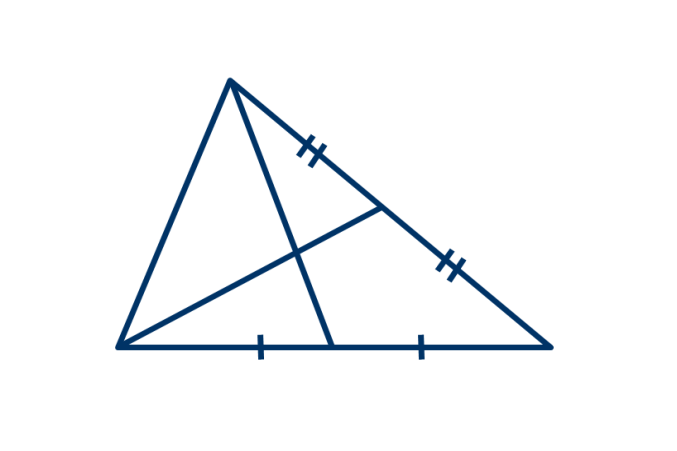
Выберите один из 4 вариантов ответа:
1) Четыре
2) Шесть
3) Восемь
4) Двенадцать
Задание 5
Вопрос:
В треугольнике АВС отрезок AD является медианой. Чему равна длина стороны ВС, если длина отрезка BD равна 3 см?
Изображение:
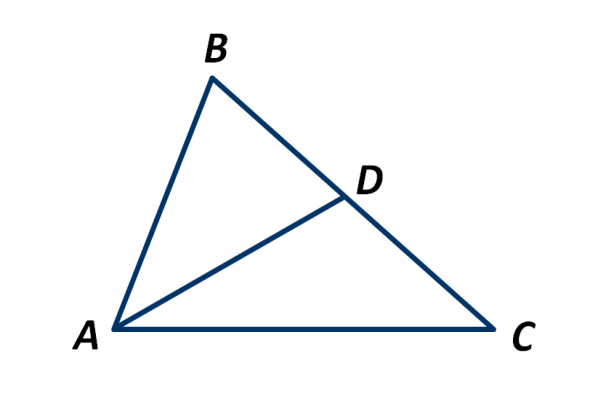
Выберите один из 4 вариантов ответа:
1) 9 см
2) 6 см
3) 5 см
4) 3 см
Задание 6
Вопрос:
Чему равна градусная мера угла ВАС, если АD – биссектриса треугольника АВС, а угол ВАD равен 35°?
Изображение:
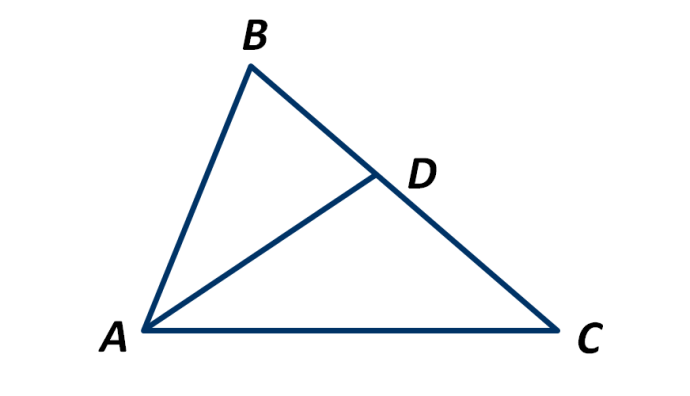
Выберите один из 4 вариантов ответа:
1) 35°
2) 90°
3) 70°
4) 45°
Задание 7
Вопрос:
Может ли точка пересечения высот лежать вне треугольника?
Выберите один из 2 вариантов ответа:
1) Может
2) Не может
Задание 8
Вопрос:
Сколько высот имеет любой треугольник?
Выберите один из 4 вариантов ответа:
1) Четыре
2) Одну
3) Две
4) Три
Задание 9
Вопрос:
Отрезок ВD – медиана треугольника АВС, отрезок ВЕ – медиана треугольника DBC. Чему равна длина отрезка ЕС, если отрезок АС равен 20 см?
Изображение:
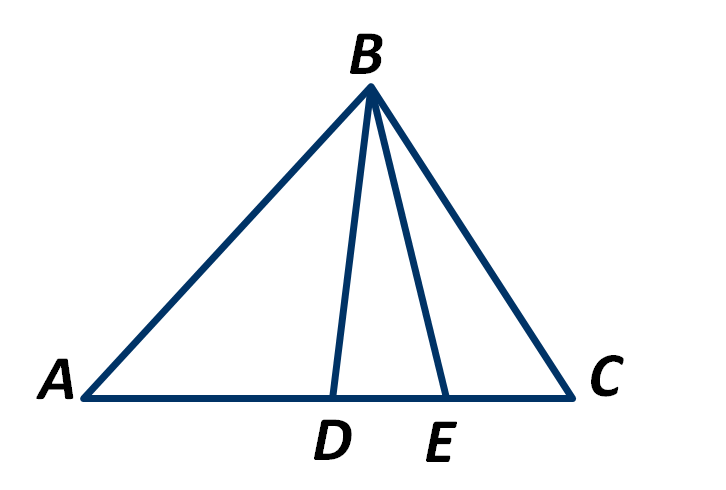
Выберите один из 4 вариантов ответа:
1) 15 см
2) 10 см
3) 5 см
4) 4 см
Задание 10
Вопрос:
Чему равна градусная мера углаАDB, если отрезок BD – высота треугольника АВС?
Выберите один из 4 вариантов ответа:
1) 30°
2) 60°
3) 90°
4) 120°
Ответы:
1) Верный ответ: "медианой".
2) Верный ответ: "высотой".
3) Верный ответ: "Биссектрисой треугольника".
4) Верный ответ: 3;
5) Верный ответ: 2;
6) Верный ответ: 3;
7) Верный ответ: 1;
8) Верный ответ: 4;
9) Верный ответ: 3;
10) Верный ответ: 3;
Итог: Молодцы ребята. Вы хорошо применяете определения и формулировки свойств геометрических фигур при решении задач.
Итак, мы с вами повторили теоретический материал прошлых уроков, который нам понадобится при изучении новой темы «Свойства равнобедренного треугольника».
III. Объяснение нового материала
Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал ещё в глубокой древности. Например, то, что в равнобедренном треугольнике, с которым мы сегодня познакомимся, углы при основании равны, было известно ещё древним вавилонянам 4000 лет назад. Равнобедренный треугольник обладает ещё рядом геометрических свойств, которые всегда имели широкое применение в практической жизни.
Выясним, какой треугольник называется равнобедренным, и какими свойствами он обладает.
Откройте тетради, запишите число, классная работа и тему сегодняшнего урока «Свойства равнобедренного треугольника»
1. Вводится понятие равнобедренного треугольника и его элементов.
Вспомните из курса математики, какой треугольник называется равнобедренным?
- Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми, а третья сторона – основанием равнобедренного треугольника.
- Назовите угол, лежащий напротив основания треугольника, назовите углы при основании равнобедренного треугольника. (слайд № 10) Изобразите данный треугольник к себе в тетрадь.
2. Вводится понятие равностороннего треугольника.
- Треугольник, все стороны которого равны, называется равносторонним.
4. Рассматриваем свойство об углах равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны.
Работа с формулировкой теоремы: разбираем, что дано, что доказать. Рассматриваем доказательство теоремы 1. Проведём биссектрису из вершины А треугольника к основанию ВС. Предлагаю учащимся продолжить доказательство самостоятельно (в процессе рассуждений, по щелчку “мыши” появляются записи на экране)
Т
еорема. В равнобедренном треугольнике углы при основании раны
 А
А
Дано: Δ АВС - ………………
Доказать: …………
В C
F
Доказательство.
-
Проведем биссектрису АF.
-
Рассмотрим ……… и ………..:
-
… …. = …….. (т.к. Δ АВС - ………………);
…. = …….. (т.к. Δ АВС - ………………);
-
……. = ………( т.к. АF - …………..Δ АВС );  ………….. = …………..
………….. = …………..
-
……….. - …………….. (по двум сторонам и углу между ними)
Тогда ……… = ………., ч.т.д.
5. Свойство биссектрисы, проведённой к основанию равнобедренного треугольника, можно предложить учащимся получить самостоятельно (это зависит от уровня подготовки класса), проведя практическую работу по группам:
- Постройте равнобедренный треугольник
- Проведите биссектрису из вершины треугольника к его основанию
- Вы знаете, что она делит угол пополам, но как вы думаете, глядя на рисунок, каким ещё свойством обладает эта биссектриса? При обсуждении подумайте:
- Любая ли биссектриса равнобедренного треугольника является ли его высотой и медианой? (Можно предложить построить все биссектрисы треугольника).
- Является ли биссектриса равнобедренного треугольника его высотой и медианой? Если да, то какая из трёх?
6. Записываем свойство в виде теоремы 2.
Т еорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой (в процессе рассуждений, по щелчку “мыши” появляются записи на экране)
еорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой (в процессе рассуждений, по щелчку “мыши” появляются записи на экране)
A Дано:
Δ АВС - ………………
AF - ……………… Δ АВС
B С Доказать: AF -………….. Δ АВС, AF -………….. Δ АВС
F
Доказательство.
Рассмотрим ……… и ………..:
-
… …. = …….. (т.к. ΔАВС - ………………);
…. = …….. (т.к. ΔАВС - ………………);
-
……. = ………( т.к. AF - …………..Δ АВС ); 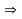 ………….…………..
………….…………..
-
……….. - ……………..
(по двум сторонам и углу между ними)
Тогда ……… = ………., AF - ……………….. Δ АВС.
Тогда 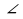 ……. =
……. = 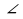 ……., а т.к.
……., а т.к. 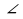 …… и
…… и 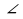 …… - смежные,
…… - смежные, 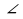 ……. =
……. = 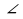 ……. = ….о, т.е. AF
……. = ….о, т.е. AF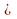 ……, значит, AF - ……………….. Δ АВС, ч.т.д.
……, значит, AF - ……………….. Δ АВС, ч.т.д.
IV. Закрепление пройденного
-
Устное решение задач
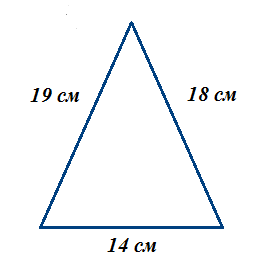
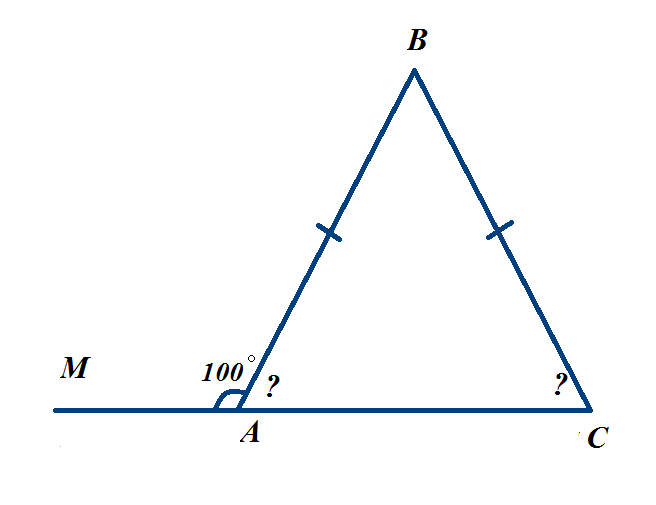
-
Треугольник АВС – равнобедренный, АС – основание, ВD – биссектриса, ∠СВD = 37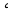 , АС = 25 см. Найдите∠В, ∠ВDС и DC.
, АС = 25 см. Найдите∠В, ∠ВDС и DC.
-
Решение задачи № 107 из учебника на доске и в тетрадях.
-
Самостоятельное решение № 112 с последующей проверкой
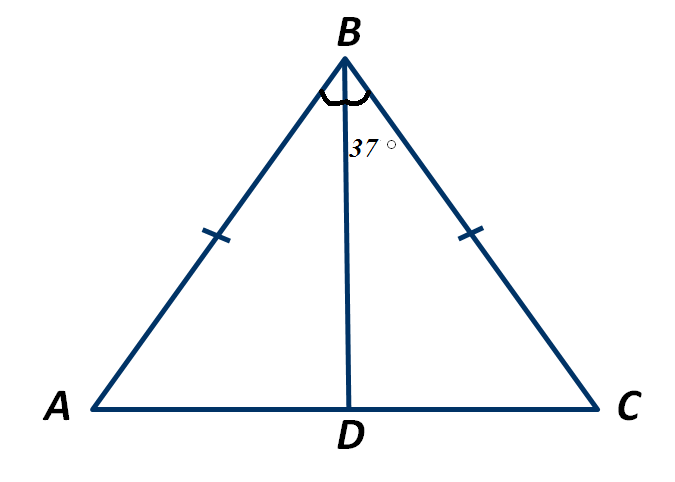
Дано: АВ=ВС, ∠1=130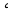 . Найдите ∠2
. Найдите ∠2
Решение:
Углы ∠ 1 и ∠АСВ – смежные, т.е∠1 + ∠АСВ=180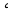 , значит
, значит
∠АСВ = 180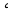 - 130
- 130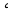 = 50
= 50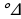 АВС – равнобедренный,
АВС – равнобедренный,
значит ∠ВАС = ∠АСВ=50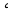 (углы при основании равнобедренного треугольника)
(углы при основании равнобедренного треугольника)
∠2 = ∠ВАС = 50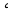 ( каквертикальные)
( каквертикальные)
Ответ: ∠ 2= 50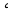
V. Итоги урока
1. Фронтальный опрос:
-
Какой треугольник называется равнобедренным?
-
Какой треугольник называется равносторонним?
-
Является ли равносторонний треугольник равнобедренным?
-
Каким свойством обладают углы равнобедренного треугольника?
-
Каким свойством обладает биссектриса равнобедренного треугольника?
-
Любая ли биссектриса обладает этим свойством? Какая?
-
Любая ли биссектриса равностороннего треугольника обладает этим свойством?
2. Домашнее задание: п.18, вопросы 10 – 18, №№ 109, 117
1












 А
А  …. = …….. (т.к. Δ АВС - ………………);
…. = …….. (т.к. Δ АВС - ………………); ………….. = …………..
………….. = ………….. ……. =
……. =  ……, значит, AF - ……………….. Δ АВС, ч.т.д.
……, значит, AF - ……………….. Δ АВС, ч.т.д.



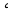 , найдите∠А и ∠С в треугольнике АВС
, найдите∠А и ∠С в треугольнике АВС


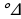 АВС – равнобедренный,
АВС – равнобедренный,

















