|
Муниципальное бюджетное общеобразовательное учреждение «Сеяхинская школа – интернат»

10 класс
Разработчик: Спирякова Екатерина Алексеевна
с. Сеяха
|
Класс: 10
Предмет: алгебра и начала анализа.
Тема урока: синус и косинус двойного угла.
Тип урока: изучение нового материала.
Педагогические задачи: рассмотреть нахождение синуса и косинуса двойного угла.
Планируемые результаты образования:
Предметные: систематизировать знания о синусе и косинусе двойного угла и уметь применять при решении различных задач.
Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД):
Регулятивные: под руководством учителя формулируют учебную задачу урока, определяют последовательность действий, осуществляют контроль собственной деятельности и деятельности партнера, при необходимости корректируют свою деятельность, способны к мобилизации волевых усилий.
Познавательные: формируют познавательную активность и мотивацию изучения математики; умения сравнивать, обобщать изучаемые факты; выделяют и формулируют познавательную цель, структурируют знания, самостоятельно создают алгоритм деятельности, развивают у учащихся самостоятельность в мышлении и учебной деятельности;
Коммуникативные: развивают эмоции учащихся путем привлечения наглядности; развивают умение грамотно излагать свои мысли, обосновывать свои действия, умеют слушать, слышать и понимать партнера, правильно выражать свои мысли в речи.
Личностные: формируют информационную культуру, работают по инструкции, демонстрируют самостоятельность, ответственность, умение сотрудничать, формируют адекватность оценки собственной деятельности, чувство гордости за свои успехи и успехи товарищей, развивают аккуратность в работе.
Методы и формы обучения: частично-поисковый, практический; индивидуальная, групповая.
Материалы и оборудование: компьютер, проектор, интерактивная доска, музыка для оргмомента
Наглядно-демонстрационный материал: презентация (Приложение 1).
Основные понятия и термины: синус, косинус, формулы.
Время: 40 минут
Структура урока
Организационный момент (1 мин.)
Актуализация знаний (5 мин.)
а) Ребус (2мин)
б) Историческая справка ( 1 мин)
в) Проверка домашнего задания ( 2 мин)
г) Подготовка к изучению нового материала (3 мин)
3. Изучение нового материала (15 мин.)
4. Физминутка (2 мин.)
Проверка усвоения знаний (Самостоятельная работа 10 мин).
Домашнее задание (1 мин.)
Рефлексия (1 мин.)
Подведение итогов урока (2 мин.)
Ход урока.
Организационная часть:
Отметить отсутствующих, привести в порядок класс.
Повторение.
1. Актуализация знаний
Слайд 2: Устно: 1.Мы продолжаем изучение главы, чтобы вспомнить отгадаем ребус.
(тригонометрия)
2. Историческая справка.
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские учёные умели предсказывать солнечные и лунные затмения. Это позволяет делать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии.
Постепенно в геометрии и астрономии установили понятия синус, косинус и тангенс угла. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.
Важный вклад в развитие тригонометрии был внесён индийской математикой в период 5-7 вв. н.э. Индийским математикам были известны соотношения sin2 α + cos2 α = 1,
cos α = sin (900 - α ).
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук
Л.Эйлера.(1707-1783). Ему принадлежит принятая, в наши дни символика.
3. Домашнее задание: Ответы на слайдах № 339(1,2)
Слайд 3: Ответы:1) cosα = - √ 1 – 3/9 = - √6/3.
2) sin α = - √ 1 – 5/9 = - 2/3, tg α = 2√5/5.
Применили при решении заданий основное тригонометрическое тождество sin2 α + cos2 α = 1.
4. Подготовка к изучению нового материала и актуализация опорных знаний
Сегодня ещё раз повторим значения синуса и косинуса наиболее чаще встречающихся углов.
На доске (карточка у каждого ученика)
2.Найдите соответствие между значениями.
|
| 1 вариант |
| 1. | sin 450 | 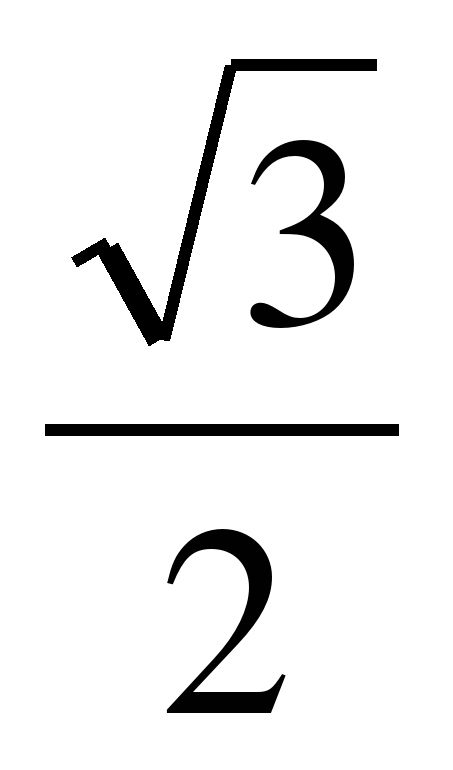
|
| 2. | cos 300 | 0 |
| 3. | sin 300 | 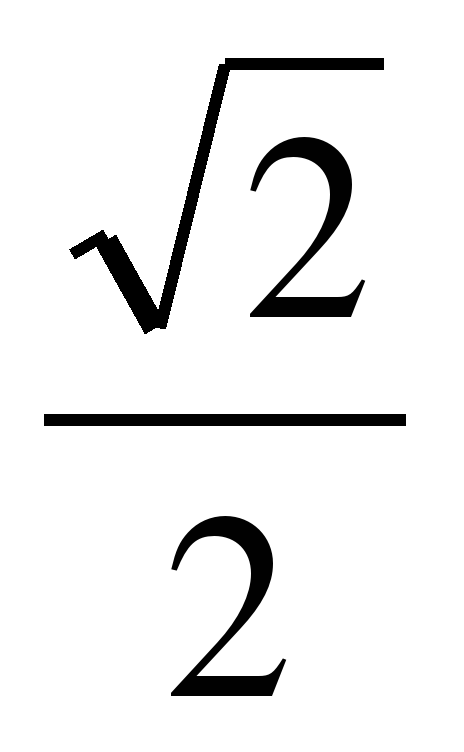
|
| 4. | cos 00 | 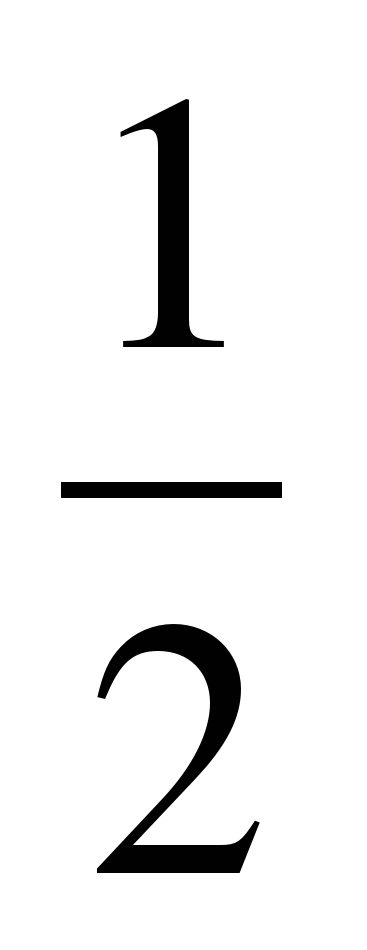
|
| 5. | sin 1800 | 1 |
2.Найдите соответствие между значениями
|
|
2 вариант |
| 1. | cos 600 | 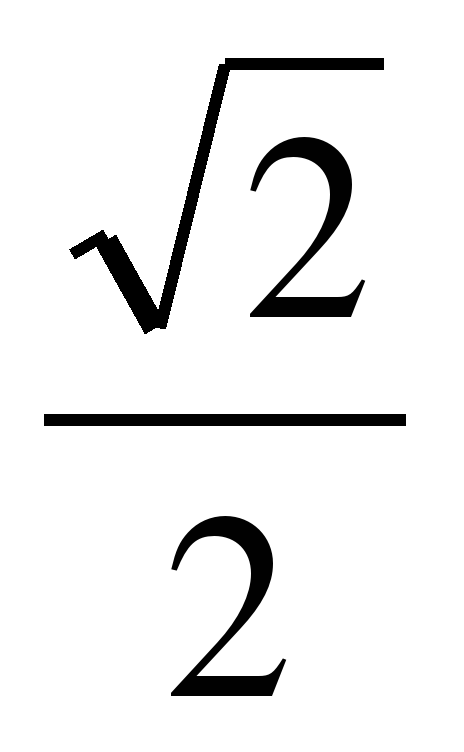
|
| 2. | sin 600 | 1 |
| 3. | cos 450 | 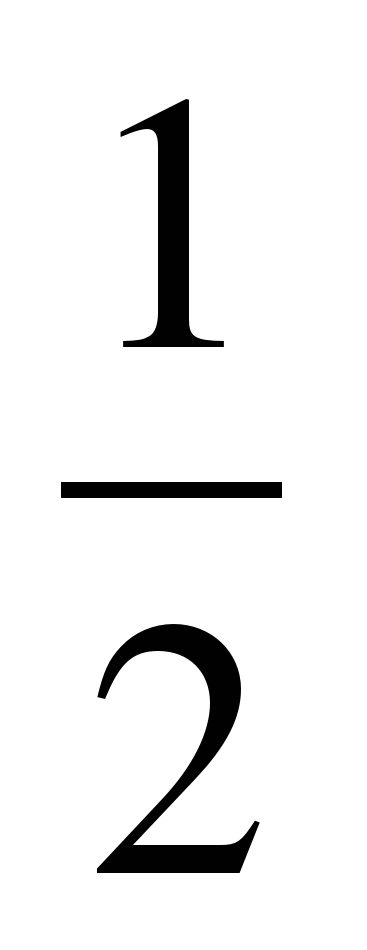
|
| 4. | sin 900 | 0 |
| 5. | cos 2700 | 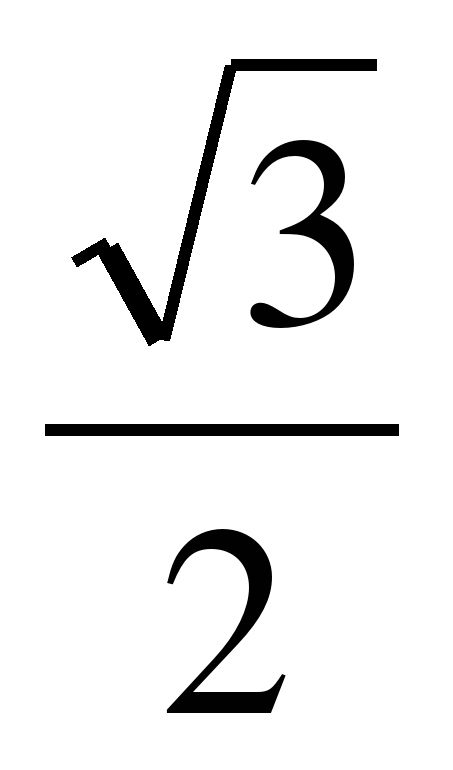
|
Изучение нового материала.
Мы, сегодня познакомимся ещё с одной формулой тригонометрии синус и косинус двойного угла.
Научимся применять формулу при выполнении преобразований тригонометрических выражений.
На доске один ученик выводит формулу синуса двойного угла из формулы синуса суммы двух углов α,
sin (α + α) = sin α cosα + cos α sin α = 2 sin α cosα
На доске один ученик выводит формулу косинуса двойного угла из формулы косинуса суммы двух углов α,
cos (α + α) = cos α cosα - sinα sinα = cos2 α – sin2 α
Слайд 4:Вывод: 1. Sin 2α =2 sin α cosα.
cos 2α = cos2 α – sin2 α.
Слайд 5: Частные случаи:
1. sin 2α =2 sin α cosα = 2 sin α sin ( ).
).
2. cos 2α = cos2 α – sin2 α = 2 cos2 α – 1= 1 –2 sin2 α.
5. Рассмотреть по учебнику страница 123.
Задача 1, Задача 2.
6. Первичное закрепление нового материала.
№ 310(2).
Дано:
сosα = -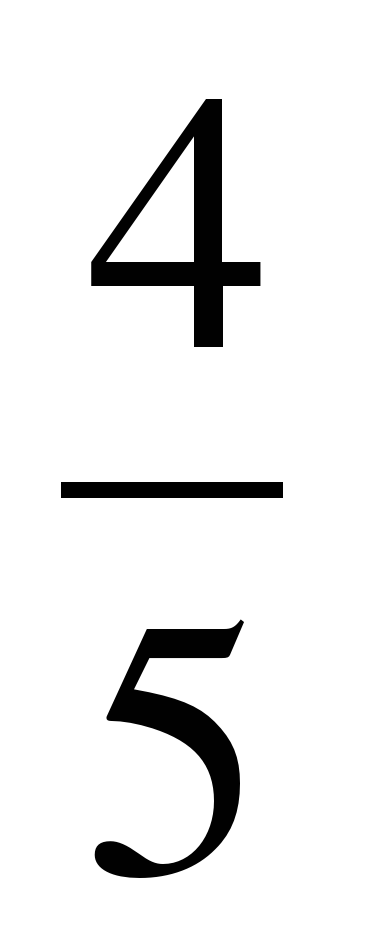 , π .
, π .
Вычислить: sin 2 α.
Решение.
sin 2α =2 sin α cosα; π , 3 четверть, sinα sin2 α + cos2 α = 1 следует, что sin2 α = 1- cos2 α,
sin α =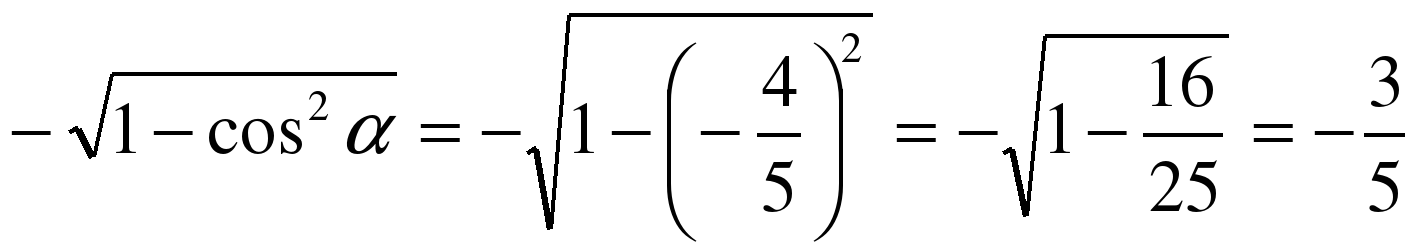 , sin α = -
, sin α = - 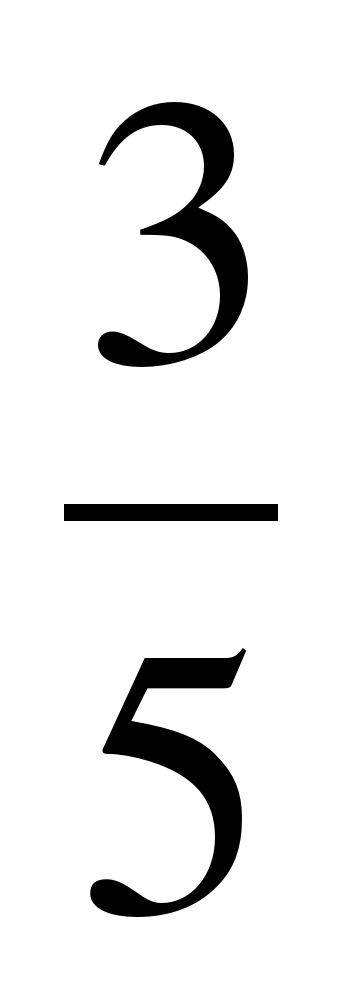 .
.
sin 2α =2 sin α cosα = 2.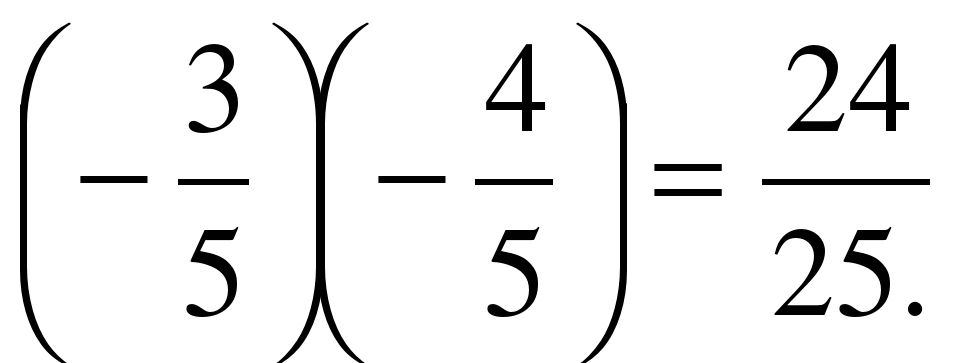 Sin 2α=
Sin 2α= 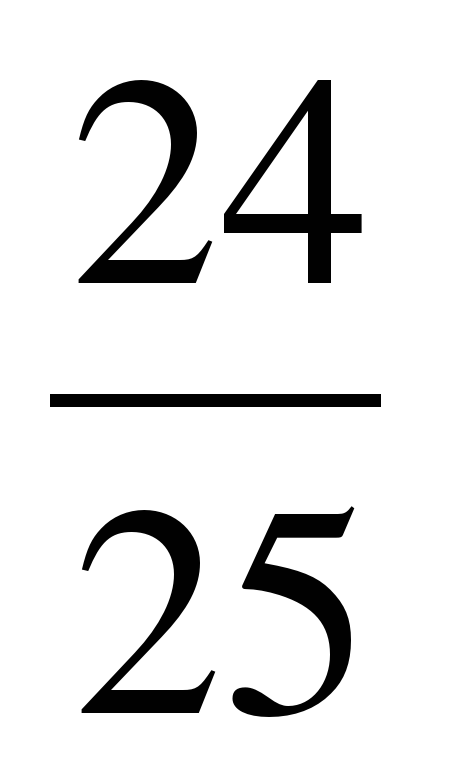 .
.
Ответ: sin 2α= 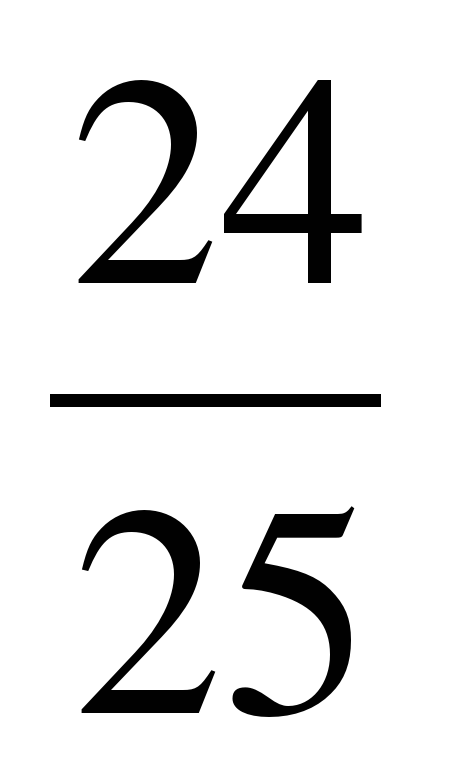 .
.
№ 311(2)
Дано: sin α = - 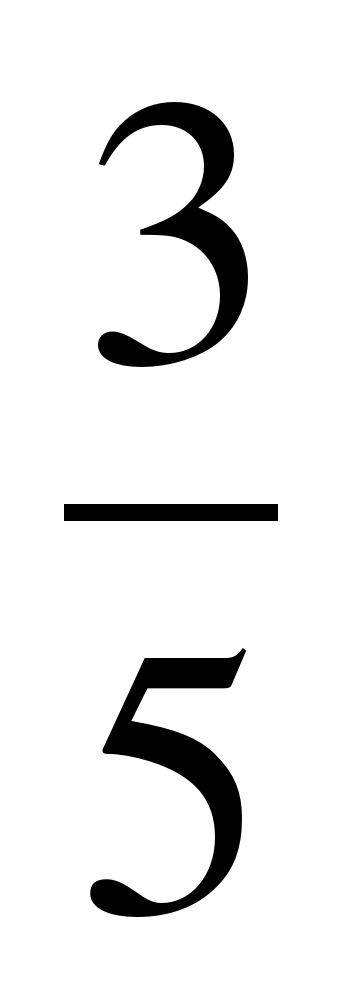 .
.
Вычислите: сos 2α.
Решение.
cos 2α = cos2 α – sin2 α, из основного тригонометрического тождества sin2 α + cos2 α = 1 следует, что
cos2 α = 1-sin2 α = 1 - 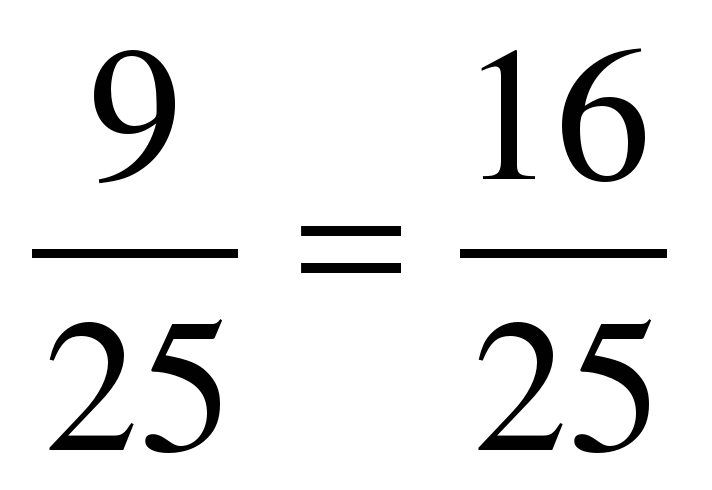 .
.
cos 2α = cos2 α – sin2 α =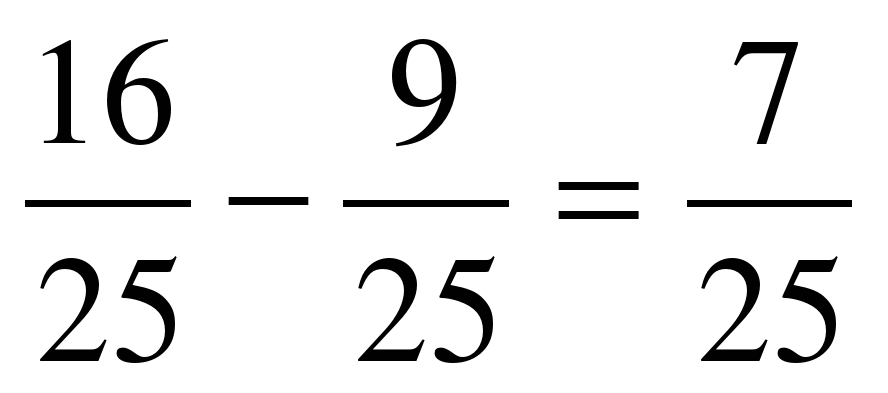
cos 2α =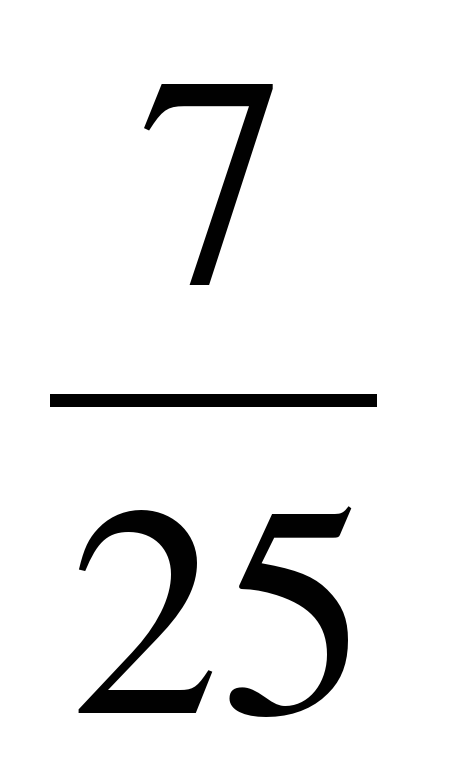 .
.
Ответ: cos 2α =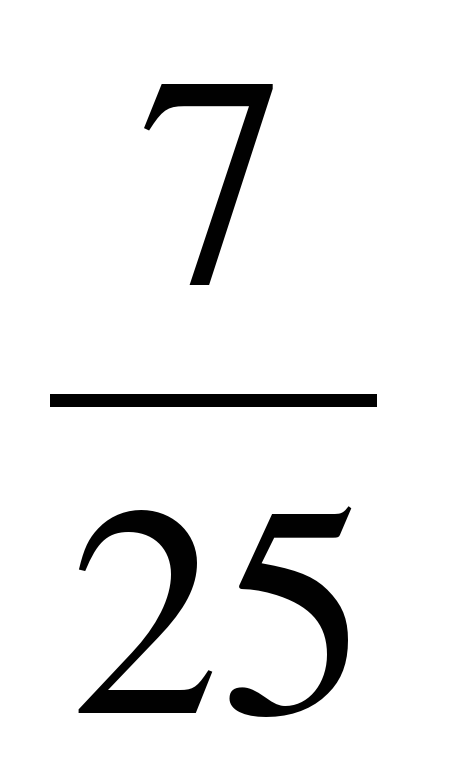 .
.
№308 (2, 4)
2) cos2 150 – sin2 150 = cos 2. 150 = cos 300= 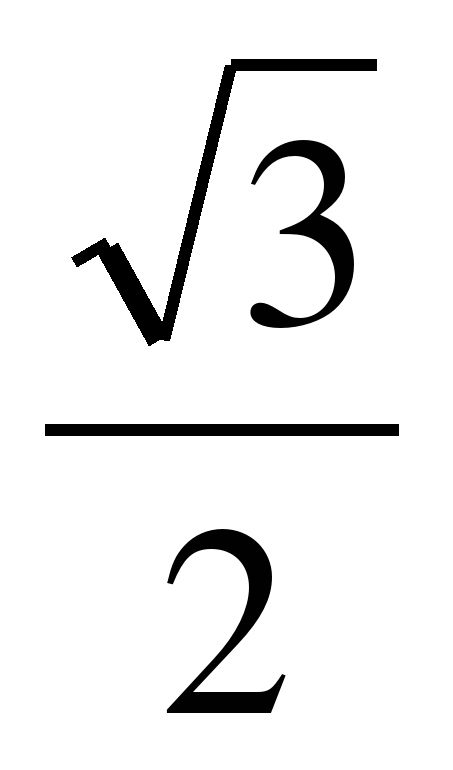 .
.
4) (cos 150 + sin 150)2 = cos2 150 +2 sin 150 cos150 + sin2 150=
= 1 + 2 sin 150 cos150 =1 + sin 300=1 + 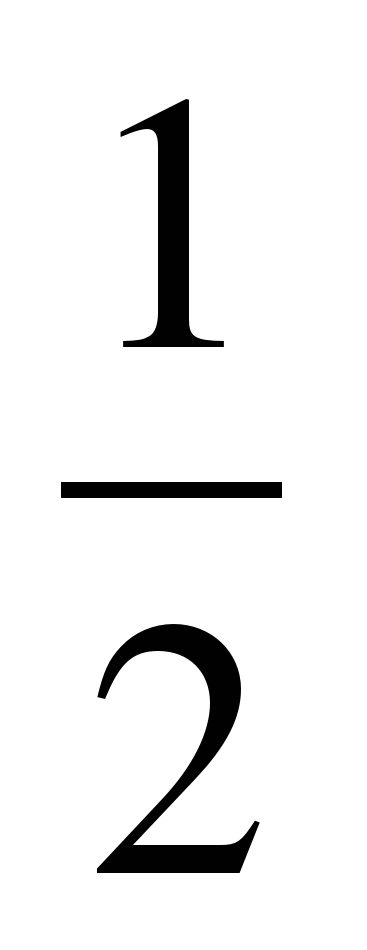 =
=  .
.
7. Вторичное закрепление. Проверка усвоения темы.
Самостоятельная работа.
Слайд 6: Вариант 1.
Вычислите:
а) 2sin π/8 cos π/8; б) (cos π/12 - sin π/12) (cos π/12 + sin π/12)
Вычислите cos 2α, sin 2α, если sin α = 0,6,
Слайд 7:
Вариант 2.
Вычислите:
а) 2sin π/12 cos π/12; б) (cos π/8 - sin π/8) (cos π/8 + sin π/8)
Вычислите sin 2α, cos 2α, если cos α = 0,8 и 3π/2 π.
Слайд 8:
Ответы: 1 вариант:1) а) ; б) 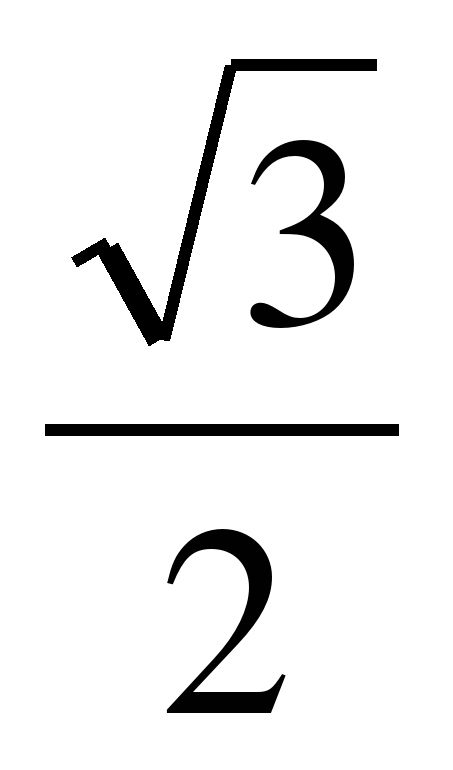 . 2) 0,28, -0,96.
. 2) 0,28, -0,96.
Ответы: 2 вариант: 1) а) ; б) 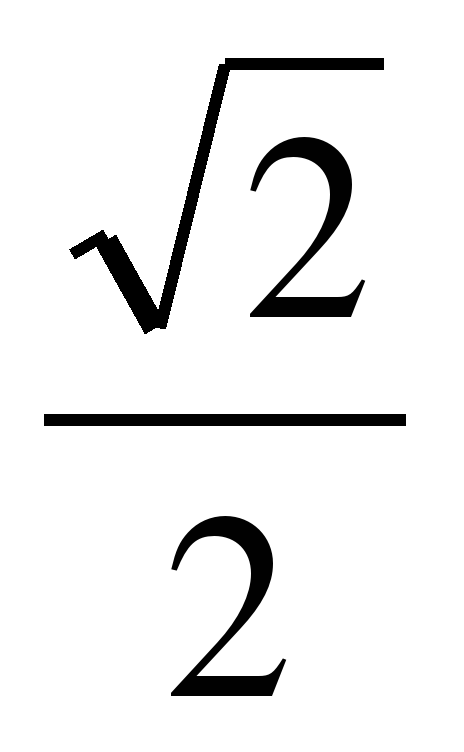 . 2)-0,96, 0,28.
. 2)-0,96, 0,28.
8. Итоги. Рефлексия:
Что я узнал нового…
Я познакомился ….
Д/з п. 25, №308(1,3), 310(1), 311(1).
Оценки. «5»- «4» - «3» -