Предмет: математика
Преподаватель: Амирханова А.К.
Тема занятия: Преобразования тригонометрических выражений.
Цели занятия.
Дидактические:
- создание условий для осознания и осмысления блока новой учебной информации;
- применение знаний в знакомой и новых учебных ситуациях;
- проверка уровня усвоения системы знаний и умений.
Образовательные:
- повторить основные формулы тригонометрии;
- выработка умений применять формулы для преобразований выражений;
- закрепление полученных знаний.
Развивающие:
- развивать логическое мышление, математическую речь, память, внимание;
- вырабатывать самостоятельность в освоении новых знаний.
Воспитательные:
- воспитывать интерес к предмету, ответственное отношение к учебному труду, волевые качества;
- формировать эмоциональную культуру и культуру общения.
Методические:
- отработать применение методов взаимоконтроля и взаимопроверки, приема взаимного целеполагания.
Формируемые личностные результаты:
- активное применение полученных знаний на практике;
- анализ производственной ситуации, быстрое принятие решений;
- выбор способов решения задач профессиональной деятельности, применительно к различным контекстам.
- использование информационных технологий в профессиональной деятельности;
- проявление доброжелательности к окружающим, деликатности, чувства такта и готовности оказать услугу каждому, кто в ней нуждается.
Тип занятия: комбинированный урок
Вид занятия: практическая работа с объяснениями педагога и с элементами самостоятельной работы
Технологии: проблемного обучения (решение примеров при систематизации знаний), развивающего обучения (тренажер)
Оборудование: учебник, опорный конспект, таблицы
Литература. Математика: алгебра и начала математического анализа, геометрия: учеб для студ. учреждений сред.проф. Образования / М.И.Башмаков. – 3-е изд., стер. – М.: Издательский центр «Академия», 2018. – 256 с.
Структура занятия.
I. Организационный момент (2 мин).
II. Целеполагание и мотивация (3 мин).
III. Актуализация знаний (15 мин).
IV. Первичное усвоение учебного материала (10 мин).
V. Осознание и осмысление учебного материала (10 мин).
VI. Систематизация знаний и умений (15 мин).
VII. Применение знаний и умений (15 мин).
VIII. Проверка уровня усвоения знаний и умений (10 мин).
IX. Информация о домашнем задании (5 мин).
X. Рефлексия (подведение итогов) (5 мин).
Ход занятия.
- Организационный момент (сообщение темы, краткого плана, постановка целей и задач занятия).
- Целеполагание и мотивация.
Определение темы и целей занятия совместно с обучающимися, акцентирование внимания обучающихся на значимость данной темы при дальнейшем изучении курса.
- Актуализация.
В ходе фронтальной работы повторяются основные теоретические моменты, необходимые на занятии, а именно:
- правила определения знаков тригонометрических функций.
(синус – в I, II к. ч. “положительный”; III, IV к. ч. “отрицательный“)
(косинус – I, IV к. ч. “положительный”; II, III к. ч. “ отрицательный “)
(тангенс, котангенс – I, III к. ч. “ положительный ”; II, IV к. ч. “ отрицательный “)
- формулы двойного аргумента, сложения аргументов и формул преобразования сумм тригонометрических функций в произведение:
- правило для запоминания формул приведения.
- приводя функцию от аргумента
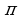 ±
±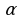 , 2
, 2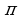 ±
±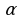 к функции аргумента
к функции аргумента 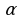 , сохраните наименование функции;
, сохраните наименование функции;
- приводя функцию от аргумента
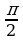 ±
±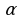 ,
, 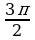 ±
±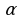 к функции аргумента
к функции аргумента 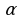 , измените наименование функции (sin на cos; и т. д.)
, измените наименование функции (sin на cos; и т. д.)
- перед полученной функцией от аргумента
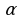 поставьте тот знак, который имела бы исходная функция от аргумента
поставьте тот знак, который имела бы исходная функция от аргумента  ±
±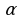 , в случае, если
, в случае, если 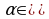 (0;
(0; 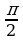 ).
).
- Первичное усвоение материала.
Составление таблицы тригонометрических формул
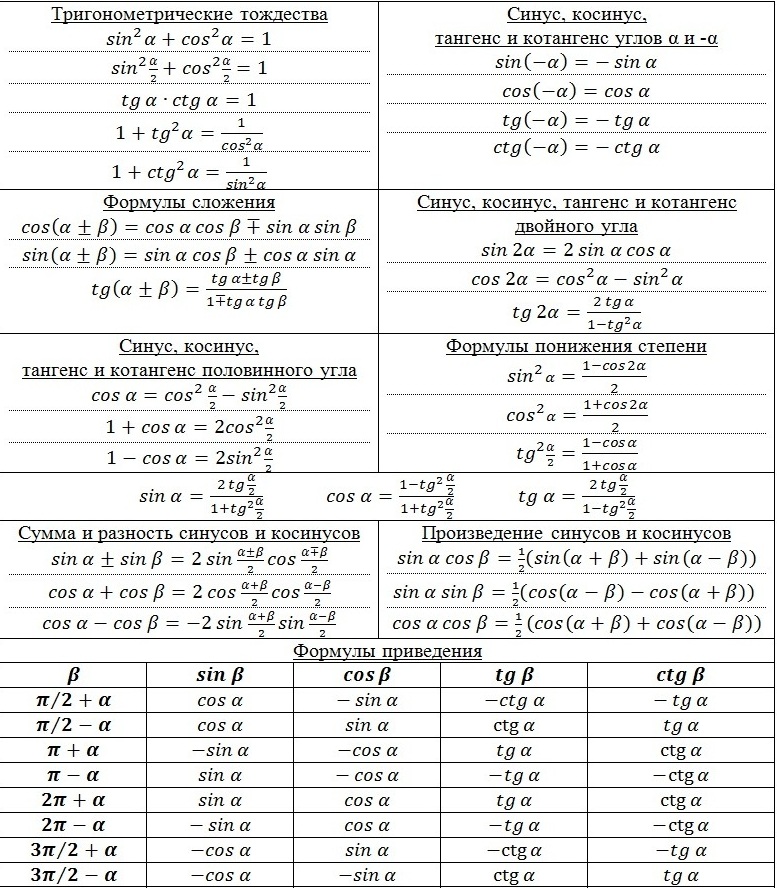
|
5. Осознание и осмысление учебного материала.
Тренажер.
Обучающиеся получают одинаковые карточки с заданиями, которые после выполнения проверяются по готовым ответам
(Упражнения, которые достаточно хорошо отработаны ранее, выполняют самостоятельно) (взаимопроверка).
Критерии оценок:
5 правильных ответов – “5”
4 правильных ответа – “4”
3 правильных ответа – “3”
- Определите знак: cos 10000
|
(“+”)
|
- Определите знак: sin 2370
|
(“–”)
|
- Вычислите: cos 2150 – sin 2150
|
(“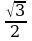 ”) ”)
|
- Вычислите: 2 sin
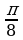 cos cos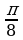
|
(“ ”) ”)
|
- Вычислите: cos1050+cos750
|
(“0”)
|
- Вычислите: sin 750
|
(“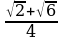 ”) ”)
|
| |
|
|
6. Систематизация знаний и умений.
Рассматриваем применение формул для преобразования тригонометрических выражений.
Решение примеров у доскисовместно с преподавателем;
контроль усвоения понятий, отработанных умений и навыков по теме.
№1. Вычислите: (используют формулы приведения)

Решение:
По формулам приведения находим:
sin 500= sin (900–400)= cos400 ; sin 200= sin (900–700)= cos700 ;
sin 400= sin (900–500)= cos500 ; cos200= cos (900–700)= sin 700.
Тогда:
 = =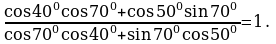
№2. Вычислите: (используют формулы сложения аргументов и двойного угла)
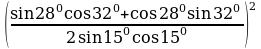
Решение:
По формулам сложения находим:
sin280cos320 + cos280sin320 = sin (280+320) = sin600 =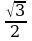 . .
По формулам двойного угла:
2sin150cos150=sin300=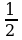 , тогда , тогда 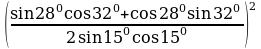 = = =3. =3.
№3. Вычислите: (используют формулы преобразования сумм тригонометрических функций в произведение)
sin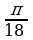 + sin + sin – sin – sin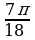
Решение:
По формулам преобразования сумм тригонометрических функций в произведение:
sin – sin – sin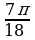 = 2cos = 2cos sin sin =–2 sin =–2 sin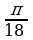 cos cos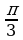 =–sin =–sin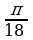 , ,
тогда sin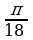 + sin + sin – sin – sin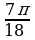 = sin = sin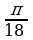 –sin –sin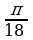 =0. =0.
№4. Вычислите: (используют формулы двойного угла)
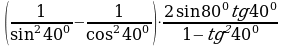
Решение:
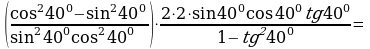 
=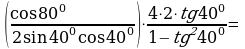 
№5. Упростите выражение:

Решение:
По формулам сложения находим:
sin = sin( = sin(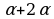 )=sin )=sin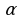 cos2 cos2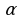 + cos + cos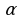 sin2 sin2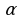 . .
По формулам преобразования сумм тригонометрических функций в произведение:
sin + sin + sin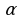 =2sin =2sin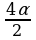 cos cos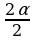 = 2sin2 = 2sin2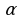 cos cos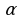 . .
Тогда  = =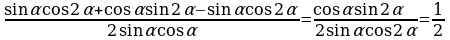 . .
№6. Упростите выражение:
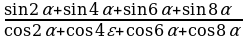
Решение:
Сгруппируем слагаемые в числителе и знаменателе дроби:
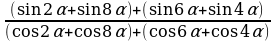
Преобразуем суммы функций в скобках в произведения:
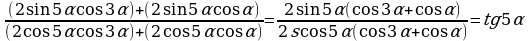 . .
7. Применение знаний и умений.
Тест с самопроверкой
8. Проверка уровня усвоения знаний и умений.
Проверка качества и уровня усвоения знаний и способов действий, а также выявление недостатков и установление причин выявленных недостатков.
Выполнение заданий для самостоятельного решения.
- Упростите:
 (ответ: 2) (ответ: 2)
- Вычислите:
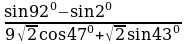 (ответ: 1/10) (ответ: 1/10)
- Упростите:
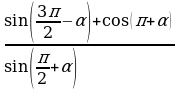 (ответ: –2) (ответ: –2)
- Упростите:
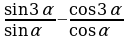 (ответ: 2) (ответ: 2)
- Подобрать ассоциации к буквам, из которых составлено слово «Тригонометрия».
- Информация о домашнем задании.
- Изучить конспект;
- Решить упражнения О1№9.70, 9.76, 9.77, 9.81.
- Рефлексия (подведение итогов занятия).
|
Просмотр содержимого документа
«Тема занятия: Преобразования тригонометрических выражений.»
Предмет: математика
Преподаватель: Амирханова А.К.
Тема занятия: Преобразования тригонометрических выражений.
Цели занятия.
Дидактические:
- создание условий для осознания и осмысления блока новой учебной информации;
- применение знаний в знакомой и новых учебных ситуациях;
- проверка уровня усвоения системы знаний и умений.
Образовательные:
- повторить основные формулы тригонометрии;
- выработка умений применять формулы для преобразований выражений;
- закрепление полученных знаний.
Развивающие:
- развивать логическое мышление, математическую речь, память, внимание;
- вырабатывать самостоятельность в освоении новых знаний.
Воспитательные:
- воспитывать интерес к предмету, ответственное отношение к учебному труду, волевые качества;
- формировать эмоциональную культуру и культуру общения.
Методические:
- отработать применение методов взаимоконтроля и взаимопроверки, приема взаимного целеполагания.
Формируемые личностные результаты:
- активное применение полученных знаний на практике;
- анализ производственной ситуации, быстрое принятие решений;
- выбор способов решения задач профессиональной деятельности, применительно к различным контекстам.
- использование информационных технологий в профессиональной деятельности;
- проявление доброжелательности к окружающим, деликатности, чувства такта и готовности оказать услугу каждому, кто в ней нуждается.
Тип занятия: комбинированный урок
Вид занятия: практическая работа с объяснениями педагога и с элементами самостоятельной работы
Технологии: проблемного обучения (решение примеров при систематизации знаний), развивающего обучения (тренажер)
Оборудование: учебник, опорный конспект, таблицы
Литература. Математика: алгебра и начала математического анализа, геометрия: учеб для студ. учреждений сред.проф. Образования / М.И.Башмаков. – 3-е изд., стер. – М.: Издательский центр «Академия», 2018. – 256 с.
Структура занятия.
I. Организационный момент (2 мин).
II. Целеполагание и мотивация (3 мин).
III. Актуализация знаний (15 мин).
IV. Первичное усвоение учебного материала (10 мин).
V. Осознание и осмысление учебного материала (10 мин).
VI. Систематизация знаний и умений (15 мин).
VII. Применение знаний и умений (15 мин).
VIII. Проверка уровня усвоения знаний и умений (10 мин).
IX. Информация о домашнем задании (5 мин).
X. Рефлексия (подведение итогов) (5 мин).
Ход занятия.
Организационный момент (сообщение темы, краткого плана, постановка целей и задач занятия).
Целеполагание и мотивация.
Определение темы и целей занятия совместно с обучающимися, акцентирование внимания обучающихся на значимость данной темы при дальнейшем изучении курса.
Актуализация.
В ходе фронтальной работы повторяются основные теоретические моменты, необходимые на занятии, а именно:
(синус – в I, II к. ч. “положительный”; III, IV к. ч. “отрицательный“)
(косинус – I, IV к. ч. “положительный”; II, III к. ч. “ отрицательный “)
(тангенс, котангенс – I, III к. ч. “ положительный ”; II, IV к. ч. “ отрицательный “)
формулы двойного аргумента, сложения аргументов и формул преобразования сумм тригонометрических функций в произведение:
приводя функцию от аргумента  ±
± , 2
, 2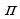 ±
± к функции аргумента
к функции аргумента  , сохраните наименование функции;
, сохраните наименование функции;
приводя функцию от аргумента 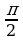 ±
± ,
, 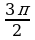 ±
± к функции аргумента
к функции аргумента  , измените наименование функции (sin на cos; и т. д.)
, измените наименование функции (sin на cos; и т. д.)
перед полученной функцией от аргумента  поставьте тот знак, который имела бы исходная функция от аргумента
поставьте тот знак, который имела бы исходная функция от аргумента 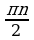 ±
± , в случае, если
, в случае, если 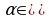 (0;
(0; 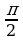 ).
).
Первичное усвоение материала.
Составление таблицы тригонометрических формул
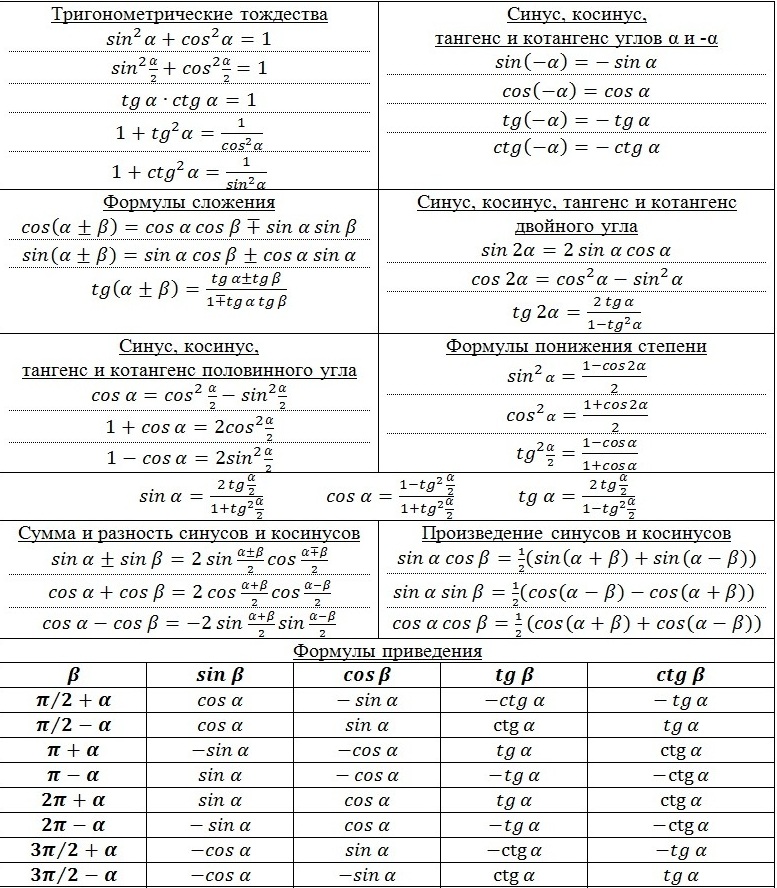
| 5. Осознание и осмысление учебного материала.
Тренажер. Обучающиеся получают одинаковые карточки с заданиями, которые после выполнения проверяются по готовым ответам (Упражнения, которые достаточно хорошо отработаны ранее, выполняют самостоятельно) (взаимопроверка). Критерии оценок: 5 правильных ответов – “5” 4 правильных ответа – “4” 3 правильных ответа – “3” Определите знак: cos 10000 | (“+”) | Определите знак: sin 2370 | (“–”) | Вычислите: cos 2150 – sin 2150 | (“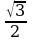 ”) ”) | Вычислите: 2 sin cos cos | (“ ”) ”) | Вычислите: cos1050+cos750 | (“0”) | Вычислите: sin 750 | (“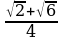 ”) ”) | 6. Систематизация знаний и умений. Рассматриваем применение формул для преобразования тригонометрических выражений.
Решение примеров у доскисовместно с преподавателем; контроль усвоения понятий, отработанных умений и навыков по теме.
№1. Вычислите: (используют формулы приведения) 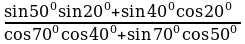
Решение: По формулам приведения находим: sin 500= sin (900–400)= cos400 ; sin 200= sin (900–700)= cos700 ; sin 400= sin (900–500)= cos500 ; cos200= cos (900–700)= sin 700. Тогда: 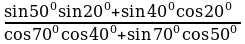 = =
№2. Вычислите: (используют формулы сложения аргументов и двойного угла) 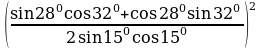
Решение: По формулам сложения находим: sin280cos320 + cos280sin320 = sin (280+320) = sin600 =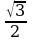 . . По формулам двойного угла: 2sin150cos150=sin300=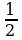 , тогда , тогда 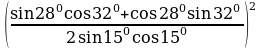 = =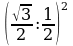 =3. =3. №3. Вычислите: (используют формулы преобразования сумм тригонометрических функций в произведение) sin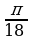 + sin + sin – sin – sin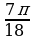 Решение: По формулам преобразования сумм тригонометрических функций в произведение: sin – sin – sin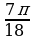 = 2cos = 2cos sin sin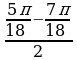 =–2 sin =–2 sin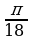 cos cos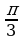 =–sin =–sin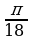 , , тогда sin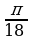 + sin + sin – sin – sin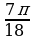 = sin = sin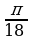 –sin –sin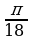 =0. =0. №4. Вычислите: (используют формулы двойного угла) 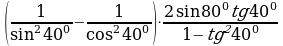
Решение: 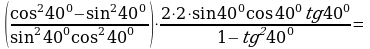 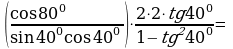
=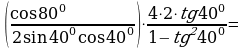 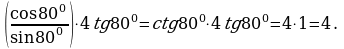 №5. Упростите выражение: 
Решение: По формулам сложения находим: sin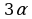 = sin( = sin(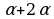 )=sin )=sin cos2 cos2 + cos + cos sin2 sin2 . . По формулам преобразования сумм тригонометрических функций в произведение: sin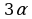 + sin + sin =2sin =2sin cos cos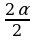 = 2sin2 = 2sin2 cos cos . . Тогда  = = . . №6. Упростите выражение: 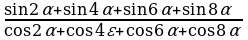
Решение: Сгруппируем слагаемые в числителе и знаменателе дроби: 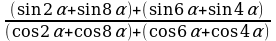
Преобразуем суммы функций в скобках в произведения: 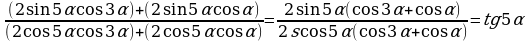 . .
7. Применение знаний и умений.
Тест с самопроверкой
8. Проверка уровня усвоения знаний и умений.
Проверка качества и уровня усвоения знаний и способов действий, а также выявление недостатков и установление причин выявленных недостатков.
Выполнение заданий для самостоятельного решения.
Упростите:  (ответ: 2) (ответ: 2) Вычислите: 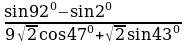 (ответ: 1/10) (ответ: 1/10) Упростите: 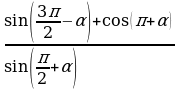 (ответ: –2) (ответ: –2) Упростите: 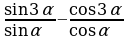 (ответ: 2) (ответ: 2)
Подобрать ассоциации к буквам, из которых составлено слово «Тригонометрия».
Информация о домашнем задании.
Изучить конспект; Решить упражнения О1№9.70, 9.76, 9.77, 9.81.
Рефлексия (подведение итогов занятия). |






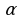 =
= )=
)=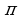 ±
±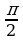 ±
±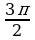 ±
± ±
±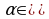 (0;
(0; 
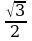 ”)
”)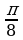 cos
cos ”)
”)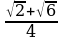 ”)
”)
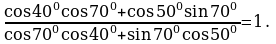
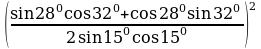
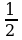 , тогда
, тогда  =3.
=3.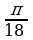 + sin
+ sin – sin
– sin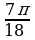
 sin
sin =–2 sin
=–2 sin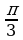 =–sin
=–sin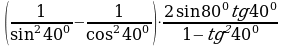
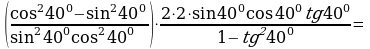

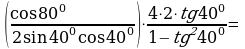


 = sin(
= sin(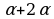 )=sin
)=sin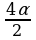 cos
cos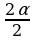 = 2sin2
= 2sin2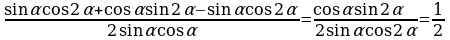 .
.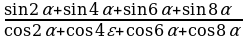
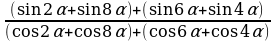
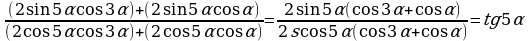 .
.
 (ответ: 2)
(ответ: 2)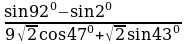 (ответ: 1/10)
(ответ: 1/10)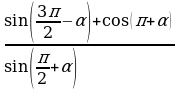 (ответ: –2)
(ответ: –2)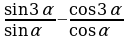 (ответ: 2)
(ответ: 2)
 sin
sin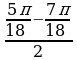 =–2 sin
=–2 sin
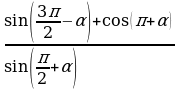 (ответ: –2)
(ответ: –2)









