Название предмета: алгебра и начала анализа
Класс: 11
УМК: «Алгебра и начала анализа» 10-11 класс, А.Г. Мордкович и др., 2013 г.
Уровень обучения: базовый
Тема урока: «Обобщение понятия о показателе степени».
Общее количество часов, отведенное на изучение темы: 2 часа
Место урока в системе уроков по теме: 1
Техническое обеспечение урока: карточки для работы у доски и самостоятельной работы.
Цель урока:
Расширить понятие степени, дать понятие степени с рациональным показателем; научить переводить степень с рациональным показателем в корень и наоборот; вычислять степени с рациональным показателем.
Развитие памяти, мышления, устного счета.
Формирование активности. ответственности, трудолюбия.
«Пусть кто-нибудь попробует вычеркнуть
из математики степени, и он увидит,
что без них далеко не уедешь»
М.В.Ломоносов
Ход урока
1. Организационный момент, проверка готовности к уроку.
2. Актуализация опорных знаний.
а) Перечислите свойства степеней с целым показателем (работа на обратной стороне доски)
Какая ошибка в записи свойств степени?


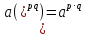
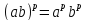
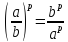
б) Повторение. Устная работа.
1) Дайте определение степени с целым показателем
2) Если 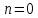 , то 150 = ?
, то 150 = ?
3) Если 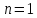 , то 751 = ?
, то 751 = ?
4) Если  , то
, то 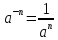 .
.
5) Вычислите 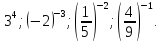
6) Сравните с единицей: 10 – 2; 420 ; (0,2)- 6 ; 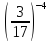
в) Проверить задание у доски.
3. Объяснение нового материала.
Во всех представленных выше заданиях, показатель степени – целое число. Как быть в случае дробного показателя? При работе с такими степенями нужно, чтобы все свойства для целочисленных степеней сохранялись.
Как вы думаете, что представляет собой число 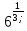 30,5;
30,5;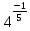 ? (выслушать мнения учеников, которые они предложат).
? (выслушать мнения учеников, которые они предложат).
Для этого надо обобщить понятие степени. Рассмотрим равенство 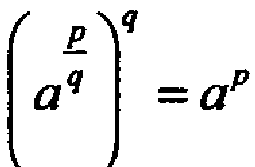 . Тогда по определению q-й степени разумно считать, что
. Тогда по определению q-й степени разумно считать, что 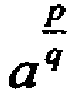 будет корнем q-й степени из числа ap.
будет корнем q-й степени из числа ap.

Пример 1.
По определению степени с рациональным показателем и свойствам корней получаем: 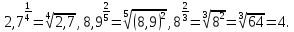
Сделаем ряд замечаний, связанных с понятием степени с рациональным показателем.
1) Для любого 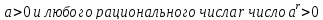 .
.
2) По основному свойству дробей рациональное число можно записать в виде 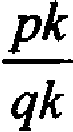 для любого натурального числа k. Тогда значение степени не зависит от формы записи рационального числа, т.к.
для любого натурального числа k. Тогда значение степени не зависит от формы записи рационального числа, т.к. 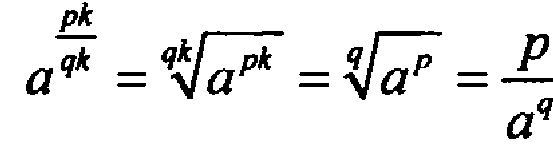 .
.
3) При a рациональная степень числа a не определена. Рассмотрим  . С другой стороны
. С другой стороны  , и тогда
, и тогда 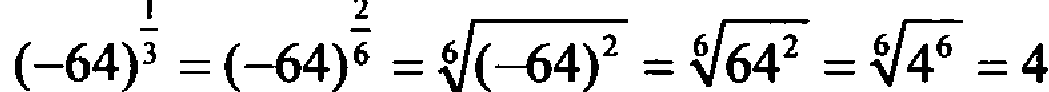 . Получаем противоречие. Для приведенного определения стеени с рациональным показателем выполняются все приведенные ранее основные свойства степеней, но только для положительных оснований.
. Получаем противоречие. Для приведенного определения стеени с рациональным показателем выполняются все приведенные ранее основные свойства степеней, но только для положительных оснований.
Итак, для любых рациональных чисел s и t и любых положительныхчисел a и b справедливы равенства:
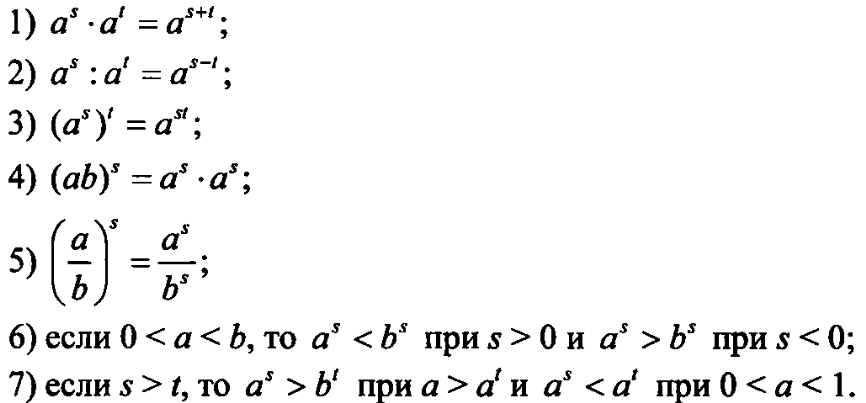
Рассмотрим применение свойств на примере.
Пример 2.
Вычислить: 
Используя ствойства степени с рациональным показателем, запишем выражение в виде
4. Первичное закрепление.
Усно выполнить №37.1 – 37.6 (а, б)
5. Подготовка к ЕГЭ. Задания из открытого банка задач. 4 учащихся работают у доски.
1. Найдите значение выражения  .
.
2. Найдите значение выражения  .
.
3. Найдите значение выражения  .
.
4. Найдите значение выражения .
5. Найдите значение выражения . Объясняет учитель.
Решение:
Здесь смущает, что основания степеней не одинаковые, даже совсем не похожие. А так ли уж они не похожи?
169 = 132; ;  .
.
А теперь применим свойство степеней №5 – произведение степеней с одинаковыми показателями
Окончательно получаем: 
Ответ: 7
6. Историческая пауза. Сведения о развитии понятия степени.
Дробные показатели степени и наиболее простые правила действии над степенями с дробными показателями встречаются у французского математика Николая Орема (1323–1382 гг.) в его труде “Алгоризм пропорций”. Известно, что Николай Шюке (1445–1500 гг.), рассматривал степени с отрицательными и нулевым показателями. Позже дробные и отрицательные, показатели встречаются в “Полной арифметике” (1544 г.) немецкого математика М.Штифеля и у Симона Стевина.Немецкий математик М.Штифель (1487–1567 гг.) дал определение а0=1 при  и ввел название показатель (это буквенный перевод с немецкого Exponent). Немецкое potenzieren означает возведение в степень.В конце ХVI века Франсуа Виет ввел буквы для обозначения не только переменных, но и их коэффициентов. Он применял сокращения: N, Q, C – для первой, второй и третьей степеней. Но современные обозначения (типа а4, а5) в XVII в ввел Рене Декарт.
и ввел название показатель (это буквенный перевод с немецкого Exponent). Немецкое potenzieren означает возведение в степень.В конце ХVI века Франсуа Виет ввел буквы для обозначения не только переменных, но и их коэффициентов. Он применял сокращения: N, Q, C – для первой, второй и третьей степеней. Но современные обозначения (типа а4, а5) в XVII в ввел Рене Декарт.
7. Самостоятельная работа. (5 мин)
Вариант 1
1. Представьте выражение в виде степени с рациональным показателем
а)  ; б)
; б)  ; в)
; в)  ;
;
2. Представьте выражение в виде корня из числа или выражения
а)  ; б)
; б)  ; в)
; в)  ;
;
3. Вычислите:
а)  ; б)
; б)  в)
в)  ; г)
; г)  ;
;
Вариант 2
1. Представьте выражение в виде степени с рациональным показателем
а)  ; б)
; б)  ; в)
; в)  ;
;
2. Представьте выражение в виде корня из числа или выражения
а)  ; б)
; б)  ; в)
; в)  ;
;
3. Вычислите:
а)  ; б)
; б)  в)
в)  ; г)
; г)  ;
;
8. Подведение итогов урока.
Домашнее задание: §37, №37.7, 37.14 (все в, г); прототипы задания 9 - №88, 89, 93, 94,100.









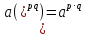
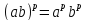
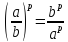
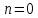 , то 150 = ?
, то 150 = ?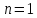 , то 751 = ?
, то 751 = ? , то
, то 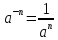 .
.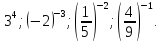
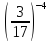
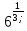 30,5;
30,5;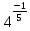 ? (выслушать мнения учеников, которые они предложат).
? (выслушать мнения учеников, которые они предложат).
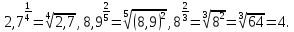
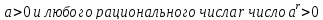 .
.