Контрольная работа для 9 класса по теме "Декартовые координаты на плоскости"

Контрольная работа № 4 по теме «Декартовые координаты на плоскости».

Вариант – 1.

1.1. Какая из точек лежит на оси абсцисс?

А) (1; 1) Б) (0; 4) В) (3; 0).

1.2. Найдите расстояние от точки В(– 6; – 3) до оси ординат.

А) – 6 Б) 3 В) – 3 Г) 6.

1.3. Найдите длину отрезка РК, если Р(2; 8), К(– 6; 2).

А) 8 Б) 10 В) 6.

1.4. Определите координаты центра и радиус окружности х² + (у + 1)² = 49.

А) О(1; 1), R = 49 Б) О(0; 1), R = 7 В) О(0; – 1), R = 7.

1.5. Найдите координаты середины отрезка АВ, если А(– 2; – 4), В( 6; 8).

А) (2; 2) Б) (– 2; 2) В) (3; 1).

1.6. Какая из точек не лежит на окружности х² + у² = 25?

А) (3; 5) Б) (4; 3) В) (– 4; 3).

1.7. Какая из прямых параллельна оси ординат?

А) х + у = 0 Б) х = – 5 В) у = 4.

1.8. Прямая пересекает окружность в двух точках, если …

А) R = d Б) R _ d В) R _ d.

2.1. Точка С(– 1; 1) – середина отрезка АВ. Найдите координаты точки А, если В(1; 9).

2.2. Докажите, что АВС с вершинами А(– 5; 0), В(5; 0) и С(0; 6) равнобедренный с основанием АВ.

2.3. Найдите координаты точки пересечения прямой 2х – 3у = 12 с осью абсцисс.

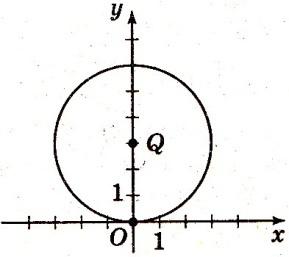
2.4. Запишите уравнение окружности с центром О и радиусом, равным длине отрезка ОQ.

Контрольная работа № 4 по теме «Декартовые координаты на плоскости».

Вариант – 2.

1.1. Какая из точек лежит на оси ординат?

А) (2; 3) Б) (0; 5) В) (1; 0).

1.2. Найдите расстояние от точки В(– 6; – 3) до оси абсцисс.

А) – 5 Б) – 2 В) 5 Г) 2.

1.3. Найдите длину отрезка АВ, если А(4; 5), В(1; 1).

А) 4 Б) 5 В) 1.

1.4. Определите координаты центра и радиус окружности (х – 5)² + у² = 4.

А) О(0; 5), R = 2 Б) О(5; 0), R = 2 В) О(– 5; 0), R = 4.

1.5. Найдите координаты середины отрезка ВС, если В(2; 4), С(4; 2).

А) (6; 6) Б) (3; 6) В) (3; 3).

1.6. Какая из точек не лежит на окружности х² + у² = 100?

А) (– 6; 8) Б) ( 6; – 8) В) ( 6; 10).

1.7. Какая из прямых параллельна оси абсцисс?

А) х – у = 5 Б) х = 8 В) у = – 3.

1.8. Прямая и окружность не имеет общих точек, если …

А) R = d Б) R _ d В) R _ d.

2.1. Точка В(5; – 2) – середина отрезка СА. Найдите координаты точки А, если С(1; – 3).

2.2. Докажите, что АВС с вершинами А(0; – 3), В(2; 3) и С(6; – 1) равнобедренный с основанием ВС.

2.3. Найдите координаты точки пересечения прямой 8х – 7у = 14 с осью ординат.

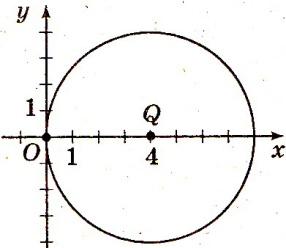
2.4. Запишите уравнение окружности с центром Q и радиусом, равным длине отрезка ОQ.

3.1. Составьте уравнение прямой, проходящей через точки (2; 3) и (4; 1).

3.2. АВСD – параллелограмм с вершинами А(– 2; 1), С(5; 2), D(0; – 6). Найдите координаты вершины В.

3.1. Составьте уравнение прямой, проходящей через точки (0; – 3) и (– 2; 1).

3.2. АВСD – параллелограмм с вершинами А(– 2; 2), В(1; 4), D(4; 5). Найдите координаты вершины С.