Итоговая контрольная работа по математике
за первое полугодие 2013-2014 учебного года (10 класс)
Вариант № 1
Ответом на задания В1–В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
В 1. В школьную библиотеку привезли книги по математике для 9-11 классов, по 50 штук для каждого класса. В шкафу 4 полки, на каждой полке помещается 10 книг. Сколько шкафов можно полностью заполнить новыми книгами по математике, если все книги одного формата?
В 2. В городе N живет 300000 жителей. Среди них 10 % детей и подростков. Среди взрослых 35% не работает (пенсионеры, домохозяйки, безработные). Сколько взрослых работает?
В 3. На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с мая по декабрь 1973 года включительно.

В 4. Для остекления веранды требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 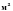 . В таблице приведены цены на стекло и на резку стекол. Сколько рублей нужно заплатить за самый выгодный заказ?
. В таблице приведены цены на стекло и на резку стекол. Сколько рублей нужно заплатить за самый выгодный заказ?
| Фирма | Стоимость стекла (руб. за 1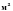 ) ) | Резка стекла (руб. за одно стекло) |
| A | 300 | 17 |
| Б | 320 | 13 |
| В | 340 | 8, бесплатно, если сумма заказа превышает 2500 рублей. |
В 5. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

В 6. В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
В 7. 1. Решите уравнение 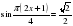 . В ответе напишите наибольший отрицательный корень.
. В ответе напишите наибольший отрицательный корень.
2. Решите уравнение 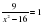 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
В 8. В треугольнике ABC AD — биссектриса, угол C равен 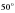 , угол CAD равен
, угол CAD равен 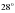 . Найдите угол B. Ответ дайте в градусах.
. Найдите угол B. Ответ дайте в градусах.
В 9. В треугольнике ABC угол C равен 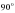 ,
, 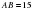 ,
, 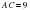 . Найдите
. Найдите  .
.
В 10. В кубе 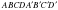 точка К — середина ребра BC, точка L — середина ребра CD, точка M — середина ребра
точка К — середина ребра BC, точка L — середина ребра CD, точка M — середина ребра 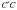 . Найдите
. Найдите 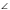 MLK. Ответ дайте в градусах.
MLK. Ответ дайте в градусах.
Ответом на задания В11–В15 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
В 11. 1. Найдите 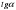 , если
, если 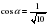 и
и 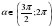 .
.
2. Вычислите 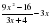 .
.
В 12. Опорные башмаки шагающего экскаватора, имеющего массу 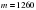 тонн, представляют собой две пустотелые балки длиной
тонн, представляют собой две пустотелые балки длиной 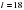 метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой
метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой 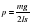 , где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте
, где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте 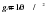 ). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
В 13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

В 14. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В 15. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ дайте в км/ч.
Для записи решений и ответов на задания С1–С6 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2 и т. д.), а затем полное обоснованное решение и ответ.
С 1. 1. Решите уравнение . Укажите количество корней уравнения, принадлежащих отрезку 
 .
.
2. а) Решите уравнение  .
.
б) Найдите все корни уравнения, принадлежащие промежутку  .
.
С 2. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Докажите, что точки А, В1 и С1 лежат на одной прямой. Найдите длину отрезка ВВ1, если СС1=15 см, АС : ВС = 2 : 3.
1







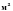 . В таблице приведены цены на стекло и на резку стекол. Сколько рублей нужно заплатить за самый выгодный заказ?
. В таблице приведены цены на стекло и на резку стекол. Сколько рублей нужно заплатить за самый выгодный заказ? 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 
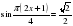 . В ответе напишите наибольший отрицательный корень.
. В ответе напишите наибольший отрицательный корень.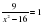 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.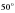 , угол CAD равен
, угол CAD равен 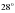 . Найдите угол B. Ответ дайте в градусах.
. Найдите угол B. Ответ дайте в градусах.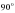 ,
, 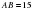 ,
, 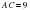 . Найдите
. Найдите  .
.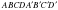 точка К — середина ребра BC, точка L — середина ребра CD, точка M — середина ребра
точка К — середина ребра BC, точка L — середина ребра CD, точка M — середина ребра 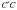 . Найдите
. Найдите 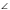 MLK. Ответ дайте в градусах.
MLK. Ответ дайте в градусах.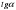 , если
, если 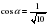 и
и 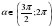 .
.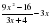 .
.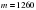 тонн, представляют собой две пустотелые балки длиной
тонн, представляют собой две пустотелые балки длиной 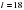 метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой
метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой 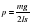 , где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте
, где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте 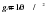 ). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.




















