Контроль знаний, умений и навыков учащихся при изучении формул сокращенного умножения
§ 1. Учебный план темы и образовательные цели изучения формул сокращенного умножения
Формулы сокращенного умножения
| № урока | Содержание урока | Пункты учебника[1] |
| 1 | Квадрат суммы и разности двух выражений. | §12, пункт 32 |
| 2 | Куб суммы и куб разности двух выражений. | §12, пункт 32 |
| 3 | Решение упражнений | §12,пункт 32 |
| 4 | Разложение на множители с помощью формул квадрата суммы и квадрата разности. | §12,пункт 33 |
| 5 | Умножение разности двух выражений на их сумму. | §13,пункт 34 |
| 6 | Разложение разности квадратов на множители. | §13,пункт 35 |
| 7 | Разложение разности квадратов на множители. | §13,пункт 35 |
| 8 | Разложение на множители суммы и разности кубов. | §13,пункт 36 |
| 9 | Использование формул сокращенного умножения для упрощения выражений. Самостоятельная работа |
|
| 10 | Решение упражнений |
|
| 11 | Формулы сокращённого умножения. Контрольная работа | §12-13, пункты 32-36 |
| 12 | Преобразование целого выражения в многочлен. | §14, пункт 37 |
| 13 | Применение различных способов для разложения на множители. | §14, пункт 38 |
| 14 | Применение различных способов для разложения на множители. | §14, пункт 38 |
| 15 | Применение различных способов для разложения на множители. | §14,пункт 38 |
| 16 | Самостоятельная работа |
|
| 17 | Решение упражнений |
|
| 18 | Преобразование целых выражений. Контрольная работа | §14, пункт 37-38 |
В данной теме вводятся новые понятия: квадрат суммы и квадрат разности двух выражений, куб суммы и куб разности двух выражений, разность квадратов, разность и сумма кубов двух выражений, формулы 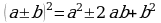 ,
, 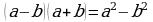 ,
, 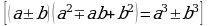 , а также применение формул сокращенного умножения в преобразованиях выражений.
, а также применение формул сокращенного умножения в преобразованиях выражений.
Основная цель – выработать умение применять в несложных случаях формулы сокращенного умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители.
В данной теме продолжается работа по формированию у учащихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам 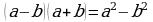 ,
, 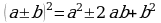 . Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
Наряду с указанными рассматриваются также формулы 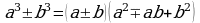 (a ± b)3 = a3 ± 3a2b + 3ab2 ± b3. Однако они находят меньшее применение в курсе. В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широко круга задач.
(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3. Однако они находят меньшее применение в курсе. В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широко круга задач.
§ 2. Система практических заданий для контроля знаний, умений и навыков при изучении формул сокращенного умножения
| № урока | Содержание урока | Вид контроля | Кто осуществляет контроль |
| 1 | Квадрат суммы и разности двух выражений. | Диагностическая работа | Взаимопроверка |
| 2 | Куб суммы и куб разности двух выражений. | Обучающая самостоятельная работа № 1 | Внешний |
| 3 | Решение упражнений | Тестовая работа № 1
| Самоконтроль
|
| 4 | Разложение на множители с помощью формул квадрата суммы и квадрата разности. | Проверочная самостоятельная работа № 1 | Внешний |
| 5 | Умножение разности двух выражений на их сумму. | Проверочная самостоятельная работа № 2 | Взаимоконтроль |
| 6 | Разложение разности квадратов на множители. | Обучающая самостоятельная работа № 2 | Самопроверка |
| 7 | Разложение разности квадратов на множители. |
|
|
| 8 | Разложение на множители суммы и разности кубов. |
|
|
| 9 | Использование формул сокращенного умножения для упрощения выражений. Самостоятельная работа | Проверочная самостоятельная работа № 3 | Внешний |
| 10 | Решение упражнений |
|
|
| 11 | Формулы сокращённого умножения. Контрольная работа | Контрольная работа № 1 | Внешний |
| 12 | Преобразование целого выражения в многочлен. |
|
|
| 13 | Применение различных способов для разложения на множители. |
|
|
| 14 | Применение различных способов для разложения на множители. | Проверочная самостоятельная работа № 4 | Взаимопроверка |
| 15 | Применение различных способов для разложения на множители. |
|
|
| 16 | Самостоятельная работа | Проверочная самостоятельная работа № 5 | Внешний |
| 17 | Решение упражнений |
|
|
| 18 | Преобразование целых выражений. Контрольная работа | Контрольная работа № 2 | Внешний |
Диагностическая работа
На первом уроке темы, перед началом объяснения нового материала рекомендуется провести диагностическую работу. Работа может представлена на слайде для решения в рабочих тетрадях с дальнейшей взаимопроверкой и устным разбором решения этих заданий. При отсутствии проектора можно провести математический диктант. Цель данной работы: повторить теоретический и практический материал по свойствам степеней, необходимый при возведении в квадрат и в куб суммы и разносности двух выражений.
| 1 вариант | 2 вариант |
-
| 92 | -
| 72 |
-
| 43 | -
| 33 |
-
| 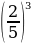
| -
| 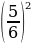
|
-
| 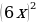
| -
| 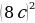
|
-
| (а6с)2 | -
| (b2c3)2 |
-
| Записать выражение: квадрат суммы 6 и с | -
| Записать выражение: квадрат разности 6 и с |
-
| Записать выражение: удвоенное произведение x и y | -
| Записать выражение: утроенное произведение x и y |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 7 | отлично |
| 5 – 6 | хорошо |
| 3 – 4 | удовлетворительно |
| 2 – 4 | неудовлетворительно |
| 1 | критично |
Обучающая самостоятельная работа № 1
После объяснения нового материала и первичного закрепления, учащимся предлагается заполнить таблицы, которые позволят учителю определить уровень понимания выученного материала. Работа предложена в двух вариантах. Учащиеся выполняют работа на карточках и выполняют самопроверку при фронтальном устном разборе заданий .
1 вариант
| Первое выражение | Второе выражение | Квадрат первого выражения | Квадрат второго выражение | Удвоенное произведение первого выражения на второе | Квадрат суммы данных выражений |
| x | y |
|
|
|
|
| n | 5 |
|
|
|
|
| 2a | 3 |
|
|
|
|
| 5c | 4b |
|
|
|
|
2 вариант
| Первое выражение | Второе выражение | Квадрат первого выражения | Квадрат второго выражение | Удвоенное произведение первого выражения на второе | Квадрат разностиданных выражений |
| n | m |
|
|
|
|
| x | 6 |
|
|
|
|
| 4b | 5 |
|
|
|
|
| 3m | 2b |
|
|
|
|
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 15-16 | отлично |
| 11 –14 | хорошо |
| 8 – 10 | удовлетворительно |
| 4 – 7 | неудовлетворительно |
| 1– 3 | критично |
Тестовая работа № 1
Для проверки домашнего задания на третьем уроке этой темы рекомендуется провести тестовую работу: «Найди правильный ответ».
| 1 вариант |
| № вопроса | Задание | Буква ответа | Ответ |
| Представьте в виде многочлена |
-
| (p – g)2 | а | p2–pg+g2 |
| б | 4x2– 6xy+9y2 |
-
| (5+n)2 | в | 25+10n+n2 |
| г | p2– 2pg+g2 |
-
| (2x – 3y)2 | д | 25+5n+n2 |
| е | 4x2– 12xy+9y2 |
| 4 | Используя формулу квадрата суммы или формулу квадрата разности, вычислите 512 | а | 102 |
| б | 2501 |
| в | 2601 |
| 5 |
Из предложенных выражений выберите те, которые тождественно равны (а – b)2 | а | (b–а)2 |
| б | (а+b)2 |
| в | (–а+b)2 |
| г | (–b +а)2 |
| д | (–а – b)2 |
-
вариант |
| № вопроса | Задание | Буква ответа | Ответ |
-
| (n+m)2 | а | m2+2mn+n2 |
| б | x2 –18x+81 |
-
| (x – 9)2 | в | 9a2 – 30ab+25b2 |
| г | x2– 9x+81 |
-
| (3a – 5b)2 | д | m2+mn+n2 |
| е | 9a2 –15ab+25b2 |
-
| Используя формулу квадрата суммы или формулу квадрата разности, вычислите 992 | а | 198 |
| б | 9801 |
| в | 9999 |
-
|
Из предложенных выражений выберите те, которые тождественно равны (а – b)2 | а | (b–а)2 |
| б | (а+b)2 |
| в | (–а+b)2 |
| г | (–b +а)2 |
| д | (–а – b)2 |
Каждому ученику раздается бланк ответов, который собирает учитель после выполнения работы. Используя тесты задания учащиеся выполняют самопроверку по готовым ответам, заранее написанные на доске.
Бланкт ответов имеет следующий вид:
| Фамилия, имя |
| № вопроса | 1 | 2 | 3 | 4 | 5 |
| Букваответа |
|
|
|
|
|
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 5 | отлично |
| 4 | хорошо |
| 3 | удовлетворительно |
| 2 | неудовлетворительно |
| 1 | критично |
Проверочная самостоятельная работа № 1
В начале четвертого урока, когда были закреплены умения применять формулы квадрата суммы и квадрата разности при упрощении выражений, можно предложить учащимся написать проверочную самостоятельную работу на сформированность умений и навыков в применении формул квадрата суммы и квадрата разности.
| 1 вариант | 2 вариант |
-
Представьте в виде многочлена | -
Представьте в виде многочлена |
-
(3a+b)2 | -
(5x – y)2 |
-
(0,7x+6)2 | -
(0,3x+4)2 |
-
(ab – 4)2 | -
(7 – xy)2 |
-
(x2+0,5y)2 | -
(0,6x – y2)2 |
-
(3a3– b2)2 | -
(2x2+b4)2 |
-
Вычислить: 492 | -
Вычислить: 612 |
-
Упростить выражение: | -
Упростить выражение: |
| (x – 5)2 – 4x(x + 3). | (y + 4)2 – 5y(y – 6). |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 7 | отлично |
| 5 – 6 | хорошо |
| 3 – 4 | удовлетворительно |
| 2 | неудовлетворительно |
| 1 | критично |
Проверочная самостоятельная работа № 2
В начале пятого урока рекомендую провести письменную работу по проверке домашнего задания и уровня усвоения умений применять формулы квадрата суммы и квадрата разности при разложении многочлена на множители.
| 1 вариант | 2 вариант |
-
Представьте трехчлен в виде квадрата двучлена: | -
Представьте трехчлен в виде квадрата двучлена: |
-
a2 + 10a +25 | -
a2 – 17a + 49 |
-
4x2 – 4x +1 | -
25y2 + 10y +1 |
-
64n2 – 80nm + 25m2 | -
100a2 – 180ab + 81b2 |
-
m8 – 6m4n5 + 9n10 | -
x10 – 6x5b4 + 9b8 |
-
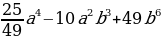
| -
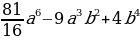
|
-
Замените звездочку одночленом так, чтобы образовалось тождество: | -
Замените звездочку одночленом так, чтобы образовалось тождество: |
-
25x10+ * + 121y6=( * + * ) | -
16x6 + * + 49y4 =( * + * ) |
-
* – 18a4b3 + * = (3b3 – * ) | -
* – 24n2b3 + * = (3n2 – * ) |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 7 – 6 | отлично |
| 4 – 5 | хорошо |
| 3 | удовлетворительно |
| 2 | неудовлетворительно |
| 1 | критично |
Обучающая самостоятельная работа № 2
На 6 уроке целесообразно провести обучающую работу, которая позволить выявить уровень усвоения формулы разности квадратов. Данную работу проверяет учитель для коррекции знаний, умений и навыков на следующем уроке
| 1 вариант | 2 вариант |
| Представьте выражение в виде многочлена: | Представьте выражение в виде многочлена: |
-
(3–а)(3+а) | -
(a–4) (a+4) |
-
(b+2а) (b–2а) | -
(y–5x) (y+5x) |
-
(2b–3а)(2b+3а) | -
(4x + 3y) (4x–3y) |
-
(1–x2) (x2+1) | -
(x3+1) (1–x3) |
-
(–4b3+b) (4b3+b) | -
(5x3+ x) (–5x3+ x) |
-
(–6b–2а) (6b –2а) | -
(–7x–3y) (7x –3y) |
-
(b2+4)(b–2)(b + 2) | -
(x2+ 9)(x+ 3)( x– 3) |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 7 – 6 | отлично |
| 4 – 5 | хорошо |
| 3 | удовлетворительно |
| 2 | неудовлетворительно |
| 1 | критично |
Проверочная самостоятельная работа № 3
Перед итоговой контрольной работой по теме «Формулы сокращенного умножения» надо провести проверочную самостоятельную работу, которая позволит определить уровень усвоения материала и выявть типовые ошибки, что даст возможность скорректировать знания, умения и навыки учащихся на следующем уроке.
| 1 вариант 1.Преобразовать в многочлен: а) (а + 5)2; в) (2b – 1)(2b + 1); б) (3y – x)2; г) (4a + 3b)(4a – 3b). 2. Разложить на множители: а) b2 – 16; в) 49a2b4 – 100c4; б) a2 + 6a + 9; г) (x + 1)2 + (x – 1)2. 3. Упростить выражение: (a – 3)2 – 3a(a – 2). 4. Решите уравнение: а) (x – 3)2 – x(x + 2,7) = 9; б) 9y2 – 25 = 0. 5. Выполнить действия: а) (x2 + 1)(x – 1)(x + 1); б) (3a2 – 6b2)(3a2 + 6b2).
| 2 вариант 1.Преобразовать в многочлен: а) (x + 4)2; в) (3a – 2)(3a + 2); б) (y – 5x)2; г) (c– 2b)(c+ 2b). 2. Разложить на множители: а) x2 – 81; в) 36x4y2 – 169c2; б) y2 – 4a + 4; г) (x + 1)2 – (x – 1)2. 3. Упростить выражение: (c + 6)2 – c(c + 12). 4. Решите уравнение: а) (x + 7)2 – (x– 4)(x + 4) = 65; б) 49y2 – 64 = 0. 5. Выполнить действия: а) (4a2 + b2)(2a – b)(2a + b); б) (b2c3 – 2a2)(b2c3 + 2a2).
|
| 3 вариант 1.Преобразовать в многочлен: а) (с – 7)2; в) (6x – 5)(6x + 5); б) (2m + n)2; г) (3d + 2y)(3d – 2y). 2. Разложить на множители: а) c2 – 25; в) 64c2d4 – 4n6; б) m2 + 8a + 16; г) (x + 2)2 + (x – 2)2. 3. Упростить выражение: (x – 5)2 – 4x(x + 3). 4. Решите уравнение: а) (x – 2)(x + 2) – x(x + 5) = – 8; б) 25y2 – 16 = 0. 5. Выполнить действия: а) (4y2 + 9)(2y – 3)(2y+ 3); б) (7m2 – 3n3)(7m2 + 3n3).
| 4 вариант 1.Преобразовать в многочлен: а) (b – 4)2; в) (1 – 8k)(1 + 8k); б) (a + 5x)2; г) (4b + 5c)(4b – 5c). 2. Разложить на множители: а) y2 – 36; в) 16m6n2 – 81x2; б) n2 – 10n + 25; г) (x + 2)2 – (x – 2)2. 3. Упростить выражение: (y + 4)2 – 5y(y – 6). 4. Решите уравнение: а) x(x – 4) + (3 – x)(3 + x) = – 6; б) 81y2 – 100 = 0. 5. Выполнить действия: а) (9c2 + d2)(3c – d)(3c + d); б) (5x4 – 7y2)(5x4 + 7y2). |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 12 – 13 | отлично |
| 9 – 11 | хорошо |
| 6 – 8 | удовлетворительно |
| 3 – 5 | неудовлетворительно |
| 1 – 2 | критично |
Контрольная работа № 1 по теме:«Формулы сокращенного умножения»
| 1 вариант | 2 вариант |
-
Представьте в виде многочлена выражение: | -
Представьте в виде многочлена выражение: |
-
(a + 7)2 | -
(с – 6)2 |
-
(3x – 4y)2 | -
(2а –3х)2 |
-
(m – 6) (m + 6) | -
(5 – а) (а + 5) |
-
(5a– 8b) (5a+8b) | -
(7х – 10у) (7х + 10у) |
-
Разложите на множители | -
Разложите на множители |
-
a2 – 9; | -
b2 – 49; |
-
25x2 – 16; | -
100 – 9 x2; |
-
b2 + 10b + 25; | -
c2 – 8c + 16; |
-
9x2 –12xy +4y2. | -
4a2 + 20ab +25b2. |
-
Упростить выражение: (x – 1)2 – (x – 3)(x + 3). | -
Упростить выражение: (x – 2)(x + 2) – (x– 5)2. |
-
Представьте в виде произведения выражение: (6a– 7)2 – (4а – 3)2. | -
Представьте в виде произведения выражение: (4b– 9)2 – (3b+8)2. |
-
Упростить выражение (а +1)(а–1) (а2 +1) – (9 +а2)2 и найти его значение при а = 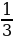 / / | -
Упростить выражение (3 –а )(3 +а) (9 +а2) + (4 +а2)2 и найти его значение при а = 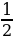 . . |
-
Решить уравнения: | -
Решить уравнения: |
-
4х2– 9 = 0; | -
25х2 – 16 = 0; |
-
(4х – 1)2– (х – 2)(х + 2) = 0. | -
(3х +1)2 – 9(х – 1)(х + 1) = 0. |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 13 | отлично |
| 10 – 12 | хорошо |
| 7 – 9 | удовлетворительно |
| 3 – 5 | неудовлетворительно |
| 1 – 2 | критично |
Проверочная самостоятельная работа № 4
На 14 уроке целесообразно провести проверочную работу, которая позволить выявить уровень навыков разложения выражений на множители с использованием вынесения общего множителя за скобки и применение формул квадрата суммы или разности , формулы разности квадратов. Данную работу проверяет учитель.
| 1 вариант | 2 вариант |
| Разложите на множители: | Разложите на множители: |
-
2y2 – 18 | 3y2 – 27 |
-
bx2 – 9b | 16a – ay2 |
-
–3a3 + 3ab2 | –2ay2 + 2a3 |
-
2x2 – 12x + 18 | 3x2 + 12x + 12 |
-
x3 – 10 x2 + 25x | 16x + 8x2 +x3 |
-
8x4y – xy4 | а5b2 + 27a2 |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 6 | отлично |
| 4 – 5 | хорошо |
| 3 | удовлетворительно |
| 2 | неудовлетворительно |
| 1 | критично |
Проверочная самостоятельная работа № 5
Перед итоговой контрольной работой по теме «Преобразование целых выражений» надо провести проверочную самостоятельную работу, которая позволит определить уровень усвоения материала и выявить типовые ошибки, что даст возможность скорректировать знания, умения и навыки учащихся на следующем уроке. Правильные решения заданий самостоятельной работы можно предложить ученикам на слайдах, где отображено пошаговое решение.
| 1 вариант | 2 вариант |
-
Разложите на множители: | -
Разложите на множители: |
-
x3 + 64y3; | -
x3 – 8y3; |
-
3a3 – 108a; | -
5x3 – 125x; |
-
a3 – 25ab2; | -
36n2m – m3; |
-
–6a2 + 26a – 54; | -
14a2 + 28a + 14; |
-
3ab + 15b – 3a – 15 ; | -
5xy – 15y – 5x + 15 ; |
-
a4 – 81; | -
a4 – 1; |
-
x3 + 3x2 – 4x – 12; | -
2m3 – m2 – 18m + 9; |
-
25 – x2 + 8xy + 16. | -
x2 – 14xy + 49 – 25. |
-
Решить уравнения: | -
Решить уравнения: |
-
3x3 – 12x=0; | -
5x3 – 20x =0; |
-
49x3 – 14x2 + x = 0; | -
36x3 + 12x2 + x = 0; |
-
x3 – 4x2 – 9x + 36 = 0. | -
x3 + 2x2 – 36x – 72 = 0. |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 10 –11 | отлично |
| 7 – 9 | хорошо |
| 4 – 6 | удовлетворительно |
| 2 – 3 | неудовлетворительно |
| 1 | критично |
Контрольная работа № 2 по теме:« Преобразование целых выражений»
| 1 вариант | 2 вариант |
-
Разложите на множители: | -
Разложите на множители: |
-
m3 + 27n3; | -
b3 – 8c3; |
-
x3 – 64xy2; | -
49x2y – y3; |
-
–3a2 + 18a – 27; | -
7a2 + 14a + 7; |
-
2ab + 10b – 2a – 10 ; | -
5ab – 15b – 5a + 15 ; |
-
a4 – 16. | -
a4 – 1. |
-
Упростить выражение (2а –1)(4а2 +2a +1) и найти его значение при а = 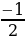 . . | -
Упростить выражение (3а +1)(9а2 – 3a +1) и найти его значение при а = 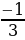 . . |
-
Разложите на множители: | -
Разложите на множители: |
-
x2 – y2 + x – y; | -
a + b + a2 – b2; |
-
4x2 – 4xy + y2 – 9; | -
9a2 – 6ab + b2 – 16; |
-
ac4 – c4 – ac2 + c2; | -
x3y2 – x3 – xy2 + x; |
-
4 – m2 +2mn – n2. | -
1 – x2 +4xy – 4y2. |
-
Решить уравнения: | -
Решить уравнения: |
-
6x3 – 24x=0; | -
2x3 – 50x =0; |
-
25x3 – 10x2 + x =0; | -
16x3 + 8x2 + x = 0; |
-
x3 – 4x2 – 9x + 36 =0. | -
x3 + 2x2 – 36x – 72 = 0. |
-
Докажите, что значение выражения 212 + 53 делится нацело на 21. | -
Докажите, что значение выражения 39 – 43 делится нацело на 23. |
Критерии оценивания:
| Количество правильный ответов | Оценка |
| 13 – 14 | отлично |
| 10 – 12 | хорошо |
| 6 – 9 | удовлетворительно |
| 3 – 5 | неудовлетворительно |
| 1 – 2 | критично |







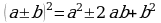 ,
, 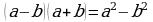 ,
, 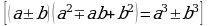 , а также применение формул сокращенного умножения в преобразованиях выражений.
, а также применение формул сокращенного умножения в преобразованиях выражений.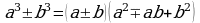 (a ± b)3 = a3 ± 3a2b + 3ab2 ± b3. Однако они находят меньшее применение в курсе. В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широко круга задач.
(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3. Однако они находят меньшее применение в курсе. В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широко круга задач.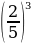
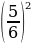
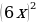
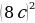
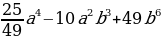
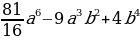
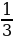 /
/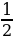 .
.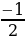 .
.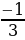 .
.


















