Контрольная работа №1 «Алгоритмизация и программирование»
Вариант 1_________________ФИО____________________________________________КЛАСС___________
Уровень А
1. Какие из фигур может нарисовать исполнитель, ели его система команд состоит из двух команд: 1. вперед на n шагов, 2. поворот на 900:
![]()
![]()





![]()


![]()
а) б) в) г) д) е)
2. Представьте, что вы сами Робот и выполните команды алгоритма. Робот находится в левом верхнем углу поля (ромб на рисунке). Посмотрите и отгадайте, что у вас получиться?
использовать Робот
алг
нач
. нц 9 раз
. . вниз
. кц
. нц 7 раз
. . вправо
. кц
. закрасить
. вверх
. нц 3 раз
. . вверх
. . закрасить
. кц
. вправо
. закрасить
. вправо
. нц 3 раз
. . вверх
. .
закрасить . кц
. вверх
. нц 3 раз
. . влево
. . закрасить
. кц
. влево
. вниз
. закрасить
. вниз
. закрасить
Кон
Уровень В
1. Исполнитель Робот. На бесконечном поле имеется стена, длины отрезков стены неизвестны. Стена состоит из одного горизонтального и трёх равных вертикальных отрезков (отрезки стены расположены буквой «Ш»). Все отрезки неизвестной длины. Робот находится в клетке, расположенной непосредственно слева от верхнего конца правого вертикального отрезка. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).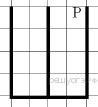

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно слева от второго вертикального отрезка. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. При исполнении алгоритма Робот не должен разрушиться. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен.
2. Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она чётна, то удаляется правый символ цепочки, а если нечётна, то в начало цепочки добавляется буква Б. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А — на Б; Б — на В и т.д., а Я — на А).
Получившаяся таким образом цепочка является результатом работы описанного алгоритма.
Например, если исходной была цепочка АВС, то результатом работы алгоритма будет цепочка ВБГТ, а если исходной была цепочка КРОТ, то результатом работы алгоритма будет цепочка ЛСП.
Дана цепочка символов СТОП. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т.е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)?
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Уровень С
1. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепашки на n шагов в направлении движения; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 КомандаЗ] означает, что последовательность команд в скобках повторится k раз.
При выполнении какого из перечисленных ниже алгоритмов на экране появился правильный треугольник?
1) Повтори 3 [Вперёд 50 Направо 20 Направо 25]
2) Повтори 3 [Вперёд 50 Направо 100 Направо 20]
3) Повтори 6 [Вперёд 50 Направо 10 Направо 20]
4) Повтори 6 [Вперёд 50 Направо 20 Направо 40]
2. Выберите ОДНО из предложенных ниже заданий:
2.1 Напишите программу рисования узора для исполнителя Робот, используя подпрограмму Крестик.

2.2 Напишите программу, которая в последовательности натуральных чисел определяет сумму всех чисел, кратных 6 и оканчивающихся на 6. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 100. Введённые числа не превышают 300. Программа должна вывести одно число: сумму всех чисел, кратных 6 и оканчивающихся на 6.
Пример работы программы:
| Входные данные | Выходные данные |
| 36 12 16 66 11 0 | 102 |
Контрольная работа №1 «Алгоритмизация и программирование»
Вариант 2_________________ФИО____________________________________________КЛАСС___________
Уровень А
1. Какие из фигур может нарисовать исполнитель, ели его система команд состоит из двух команд: 1. вперед на n шагов, 2. поворот на 450:


![]()



![]()
а) б) в) г) д) е)
2. Представьте, что вы сами Робот и выполните команды алгоритма. Робот находится в левом верхнем углу поля (ромб на рисунке). Посмотрите и отгадайте, что у вас получиться?
Использовать Робот
алг
нач
. нц 3 раз
. . вправо
. кц
. нц 8 раз
. . вниз
. . закрасить
. кц
. нц 7 раз
. .
вправо . . вверх
. . закрасить
. кц
. нц 7 раз
. . вниз
. . закрасить
. кц
Кон
Уровень В
1. Исполнитель Робот. На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От нижнего конца стены вправо отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной над правым краем горизонтальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).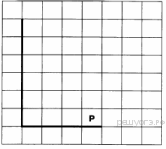

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены и примыкающие к ней. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.
2. Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она нечётна, то дублируется средний символ цепочки символов, а если четна, то в начало цепочки добавляется буква С. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А — на Б, Б — на В и т. д., а Я — на А). Получившаяся таким образом цепочка является результатом работы алгоритма.
Например, если исходной была цепочка КОТ, то результатом работы алгоритма будет цепочка ЛППУ, а если исходной была цепочка ВАНЯ, то результатом работы алгоритма будет цепочка ТГБОА.
Дана цепочка символов КОМ. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)? Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.
Уровень С
1. Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 5 paз
Сместиться на (0, 1) Сместиться на (−2, 3) Сместиться на (4, −5) Конец
Каковы координаты точки, с которой Чертёжник начинал движение, если в конце он оказался в точке с координатами (−1, −1)?
1) (−11, 4) 2) (4, −11) 3) (8, 22) 4) (22, 8)
2. Выберите ОДНО из предложенных ниже заданий:
2.1 Напишите программу рисования узора для исполнителя Робот, используя подпрограмму БукваС.
2.2 Напишите программу для решения следующей задачи. Камера наблюдения регистрирует в автоматическом режиме скорость проезжающих мимо неё автомобилей, округляя значения скорости до целых чисел. Необходимо определить максимальную зарегистрированную скорость автомобиля. Если скорость хотя бы одного автомобиля была меньше 30 км/ч, выведите «YES», иначе выведите «N0».
Программа получает на вход число проехавших автомобилей N (1
Пример работы программы:
| Входные данные | Выходные данные |
| 4
74
69
63
66 | 74
NO |
Контрольная работа №1 «Алгоритмизация и программирование»
Вариант 3_________________ФИО____________________________________________КЛАСС___________
Уровень А
1. Какие из фигур может нарисовать исполнитель, ели его система команд состоит из двух команд: 1. назад на n шагов, 2. поворот на 300:




![]()

![]()
а) б) в) г) д) е)
2. Представьте, что вы сами Робот и выполните команды алгоритма. Робот находится в левом верхнем углу поля (ромб на рисунке). Посмотрите и отгадайте, что у вас получиться?
Использовать Робот
алг
нач
. нц 3 раз
. . вправо
. кц
. нц 7 раз
. . вниз
. кц
нц 6 раз
. . закрасить
. . вправо
. кц
. нц 7 раз
. .
вверх . . закрасить
. кц
. нц 7 раз
. . влево
. . закрасить
. кц
Кон
Уровень В
1. Исполнитель Робот. На бесконечном поле имеются четыре стены, соединённые между собой, которые образуют прямоугольник. Длины стен неизвестны. В левой вертикальной стене есть ровно один проход, в нижней горизонтальной стене
также есть ровно один проход. Проход не может примыкать к углу прямоугольника. Точные места проходов и ширина проходов неизвестны. Робот находится около нижнего конца левой вертикальной стены, снаружи прямоугольника и выше нижней стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные вдоль стен прямоугольника с внутренней стороны. Проходы должны остаться незакрашенными.
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера прохода внутри стены.
2. Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Если количество букв в цепочке символов чётно, то из цепочки удаляется первая буква. В противном случае в конец цепочки добавляется символ А. Затем в полученной цепочке символы попарно меняются местами (первый — со вторым, третий — с четвёртым, и т. д.). Если в цепочке нечётное количество символов, последний символ остается на своём месте. Получившаяся таким образом цепочка является результатом работы алгоритма. Например, если исходной цепочкой была цепочка 2МД, то результатом работы алгоритма будет цепочка Д2, а если исходной цепочкой была 5Ф, то результатом работы алгоритма будет цепочка Ф5А.
Дана цепочка символов Б7В92Р. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (то есть применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)?
Уровень С
1. Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на(2, −3) переместит Чертёжника в точку (6, −1). Запись
Повтори k раз Команда1 Команда2 КомандаЗ Конец
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз. Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (3, 3) Сместиться на (1,−2) Конец
Сместиться на (−8, 12)
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −4) 2) Сместиться на (4,−13)
3) Сместиться на (2, 4) 4) Сместиться на (−8, −16)
2. Выберите ОДНО из предложенных ниже заданий:
2.1 Напишите программу рисования узора для исполнителя Робот, используя подпрограмму Квадрат.
2.2 Напишите программу, которая в последовательности натуральных чисел определяет минимальное чётное число. Программа получает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда имеется чётное число. Количество чисел не превышает 1000. Введённые числа не превышают 30 000.
Программа должна вывести одно число — минимальное чётное число.
Пример работы программы:
| Входные данные | Выходные данные |
| 4 3 20 6 8 | 6 |
Контрольная работа №1 «Алгоритмизация и программирование»
Вариант 4_________________ФИО____________________________________________КЛАСС___________
Уровень А
1. Какие из фигур может нарисовать исполнитель, ели его система команд состоит из двух команд: 1. назад на n шагов, 2. поворот на 1000:




![]()

![]()
а) б) в) г) д) е)
2. Представьте, что вы сами Робот и выполните команды алгоритма. Робот находится в левом верхнем углу поля (ромб на рисунке). Посмотрите и отгадайте, что у вас получиться?
Использовать Робот
алг
нач
. нц 3 раз
. . вправо
. кц
. нц 6 раз
. . вниз
. кц
нц 3 раз
. . закрасить
. . вправо
. . вверх
. кц
. нц 3 раз
. .
вниз . . закрасить
. кц
. нц 6 раз
. . влево
. кц
. . закрасить
Кон
Уровень В
1. Исполнитель Робот. На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От нижнего конца стены вправо отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной над правым краем горизонтальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, выше горизонтальной стены и примыкающие к ним, кроме угловой клетки. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
2. Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она чётна, то в начало цепочки символов добавляется символ А, а если нечётна, то последний символ цепочки удаляется. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А — на Б, Б — на В и т. д., а Я — на А). Получившаяся таким образом цепочка является результатом работы алгоритма.
Например, если исходной была цепочка СОН, то результатом работы алгоритма будет цепочка ТП, а если исходной была цепочка УМ, то результатом работы алгоритма будет цепочка БФН.
Дана цепочка символов ПОЛЁТ. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)? Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.
Уровень С
1. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепашки на n шагов в направлении движения; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 КомандаЗ] означает, что последовательность команд в скобках повторится k раз.
Черепашке был дан для исполнения следующий алгоритм: Повтори 9 [Вперёд 70 Направо 90]. Какая фигура появится на экране?
1) незамкнутая ломаная линия 2) правильный девятиугольник
3) правильный восьмиугольник 4) правильный четырёхугольник
2. Выберите ОДНО из предложенных ниже заданий:
2.1 Напишите программу рисования узора для исполнителя Робот, используя подпрограмму Крестик.

2.2 Напишите программу для решения следующей задачи. Камера наблюдения регистрирует в автоматическом режиме скорость проезжающих мимо неё автомобилей, округляя значения скорости до целых чисел. Необходимо определить среднюю зарегистрированную скорость всех автомобилей. Если скорость хотя бы одного автомобиля была не меньше 60 км/ч, выведите «YES», иначе выведите «NO».
Программа получает на вход число проехавших автомобилей N (1 ≤ N ≤ 30), затем указываются их скорости. Значение скорости не может быть меньше 1 и больше 300. Программа должна сначала вывести среднюю скорость с точностью до одного знака после запятой, затем «YES» или «NO».
Пример работы программы:
| Входные данные | Выходные данные |
| 4
74
69
63
96 | 75.5
YES |
Ответы
Вариант 1
Уровень А: 1. Б,г,е
2.
Уровень В. 2. ВУФР
Уровень С: 1. 2
Вариант 2
Уровень А: 1. В, е
Уровень В: 2. ТМРРО
Уровень С: 1. 1
Вариант 3
Уровень А: 1. Б, в, е 2.
Уровень В: 2. 97РВА2
Уровень С: 1. 1
Вариант 4
Уровень А: 1. е
2.
Уровень В. 2. 1
Уровень С 1. БСРНЗ