А дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ
Комитет по образованию
МАОУ «Средняя общеобразовательная школа № 57 г.Улан-Удэ
имени А. Цыденжапова»
Контрольно-измерительные материалы по предмету «Геометрия» для 8 класса
| Входная диагностика. | 1 вариант | 2 вариант. | | 1). В равнобедренном треугольнике АВС с основанием АС угол В равен 42 0. Найдите два других угла треугольника АВС.
2). Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС 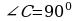 , , 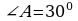 , АС = 10 см , СD , АС = 10 см , СD АВ, DE АВ, DE  АС. Найдите АЕ. АС. Найдите АЕ.
4). В треугольнике МРК угол Р составляет 60 0углаК, а угол М на 40 больше угла Р. Найдите угол Р. | 1). В равнобедренном треугольнике АВС с основанием АС сумма углов А и С равна 1560. Найдите углы треугольника АВС.
2). Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС 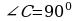 , , 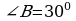 , ВС = 18 см , СК , ВС = 18 см , СК  АВ, КМ АВ, КМ  ВС. Найдите МВ. ВС. Найдите МВ.
4). В треугольнике BDE угол В составляет 30 0 угла D, а угол Е на 19 0больше угла D. Найдите угол В.
|
|
Контрольная работа №1
Тема: «Четырёхугольники»
Вариант – 1
1) Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол между диагоналями, если угол АВО = 30º.
2) В параллелограмме КМNР проведена биссектриса угла МКР, которая пересекает сторону МN в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный.
б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.
Вариант – 2
1) Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР= 80º
2) На стороне ВС параллелограмма АВСД взята точка М так, что АВ = ВМ.
а) Докажите, что АМ – биссектриса угла ВАД.
б) Найдите периметр параллелограмма, если СД = 8 см, СМ = 4 см.
Контрольная работа №2
Тема: «Площадь»
Вариант – 1
1) Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150º. Найдите площадь параллелограмма.
2) Сторона треугольника равна 5 см, а высота, проведённая к ней, в два раза больше стороны. Найдите площадь треугольника.
3) Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.
4) Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.
5) Площадь прямоугольной трапеции равна120 см², а её высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
Вариант – 2
1) Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны параллелограмма, если его площадь равна 108 см².
2) Сторона треугольника равна 12 см, а высота, проведённая к ней, в три раза меньше. Найдите площадь треугольника.
3) Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь прямоугольного треугольника.
4) Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр.
5) Найдите площадь трапеции АВСД с основаниями АД и ВС, если АВ = 12 см, ВС = 14 см, АД = 30 см, угол В равен 150º.
Контрольная работа №3
Тема: «Подобные треугольники»
Вариант – 1


 1) На рисунке АВ ║СД. А В
1) На рисунке АВ ║СД. А В
а) Докажите, что АО : ОС = ВО : ОД.
б) Найдите АВ, если ОД = 15 см, ОВ = 9 см, СД = 25 см.
Д С
2) Найдите отношение площадей треугольников АВС и КМN, если АВ =8 см, ВС=12 см, АС= 16 см, МN=15 см, NК=20 см.
В
 Вариант – 2
Вариант – 2
 1) На рисунке МN ║АС. MN
1) На рисунке МN ║АС. MN
а) Докажите, что АВ ∙ ВN = СВ ∙ ВМ. AC
б) Найдите МN, если АМ=6 см, ВМ=8 см, АС=21 см
2) Даны стороны треугольника РQR и АВС: РQ=16 см, QR=20 см, РR=28 см и АВ=12 см, ВС=15 см, АС=21см.
Найдите отношение площадей этих треугольников.
Контрольная работа №4
Тема: «Соотношение между сторонами и углами прямоугольного треугольника»
Вариант – 1
1) В прямоугольном треугольнике АВС угол А= 90º, АВ=20 см, высота АД равна 12 см. Найдите АC и cosC.
2) Диагональ ВД параллелограмма АВСД перпендикулярна к стороне АД. Найдите площадь параллелограмма АВСД, если АВ=12 см, угол А=41º.
Вариант – 2
1) Высота ВД прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок ДС, равный 18 см. Найдите АВ и cosA.
2) Диагональ АС прямоугольника АВСД равна 3 см и составляет со стороной АД угол в 37º. Найдите площадь прямоугольника АВСД.
Контрольная работа №5
Тема: «Окружность»
Вариант – 1
1) Через точку А окружности проведены диаметр АС и две хорды АВ и АД, равные радиусу этой окружности. Найдите углы четырёхугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.
2) Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант – 2
1) Отрезок ВД – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырёхугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.
2) Высота, проведённая к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Итоговая контрольная работа по геометрии 8 класс
1 вариант
1. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.
2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.
3. В равнобедренной трапеции боковая сторона равна 13 см, основания 10 см и 20 см. Найдите площадь трапеции.
4. В треугольнике АВС прямая MN , параллельная стороне АС, делит сторону ВС на отрезкиBN=15 см и NC=5 см, а сторону АВ на ВМ и АМ. Найдите длину отрезка MN, если АС=15 см.
5. В прямоугольном треугольнике АВС  =90°, АС=8 см,
=90°, АС=8 см,  =45°. Найдите:
=45°. Найдите:
а)АС; б) высоту СD, проведенную к гипотенузе.
6. Дан прямоугольный треугольник АВС, у которого  С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и  А=60°. Найдите:
А=60°. Найдите:
а) остальные стороны ∆АВС
б) площадь ∆АВС
в) длину высоты, опущенной из вершины С.
2 вариант
1. В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.
2. В параллелограмме АВСД АВ=8 см, АД=10 см,  =30°. Найдите площадь параллелограмма.
=30°. Найдите площадь параллелограмма.
3. В прямоугольной трапеции АВСД боковая сторона равна АВ=10 см, большее основание АД= 18 см,  =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.
4. В треугольнике АВС со сторонами АС=12 см и АВ=18 см проведена прямая MN, параллельная АС, MN=9 см. Найдите ВМ.
5. В прямоугольном треугольнике АВС  =90°, АС=8 см,
=90°, АС=8 см,  =45° . Найдите:
=45° . Найдите:
а)АВ; б) высоту СD, проведенную к гипотенузе.
6. Дан прямоугольный треугольник АDС, у которого  D-прямой, катет AD=3 см и
D-прямой, катет AD=3 см и  DАC=30°. Найдите:
DАC=30°. Найдите:
а) остальные стороны ∆АDС
б) площадь ∆АDС
в) длину высоты, проведенной к гипотенузе.
КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ НА КОНЕЦ ГОДА
| 1 | Объясните, какая фигура называется многоугольником. Назовите элементы многоугольника. |
| 2 | Какой многоугольник называется выпуклым? |
| 3 | Выведите формулу для вычисления суммы углов выпуклого n-угольника. |
| 4 | Чему равна сумма углов выпуклого четырехугольника? |
| 5 | Дайте определение параллелограмма, ромба, прямоугольника, трапеции, квадрата. |
| 6 | Сформулируйте и докажите свойства параллелограмма. |
| 7 | Сформулируйте и докажите признаки параллелограмма. |
| 8 | Сформулируйте и докажите свойство прямоугольника. |
| 9 | Сформулируйте и докажите свойств диагоналей ромба. |
| 10 | Сформулируйте и докажите свойства квадрата. |
| 11 | Введите понятия осевой и центральной симметрии. Приведите примеры фигур, обладающих осевой и центральной симметрией. |
| 12 | Расскажите, как измеряются площади многоугольников. |
| 13 | Сформулируйте основные свойства площадей многоугольников. |
| 14 | Сформулируйте и докажите теорему о вычислении площади прямоугольника. |
| 15 | Сформулируйте и докажите теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника. |
| 16 | Сформулируйте и докажите теорему об отношении площадей треугольников, имеющих равные углы.. |
| 17 | Сформулируйте и докажите теорему о вычислении площади трапеции. |
| 18 | Сформулируйте и докажите теорему о вычислении площади ромба. |
| 19 | Сформулируйте и докажите теорему Пифагора и обратную ей теорему. |
| 20 | Дайте определение подобных треугольников. |
| 21 | Сформулируйте и докажите теорему об отношении площадей подобных треугольников. |
| 22 | Сформулируйте и докажите признаки подобия треугольников. |
| 23 | Какой отрезок называется средней линией треугольника. Сформулируйте и докажите теорему о средней линии треугольника. |
| 24 | Сформулируйте и докажите утверждение о точке пересечения медиан треугольника. |
| 25 | Сформулируйте и докажите утверждения о пропорциональных отрезках в прямоугольном треугольнике. |
| 26 | Что такое коэффициент подобия? |
| 27 | Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? |
| 28 | Какое равенство называется основным тригонометрическим тождеством? |
| 29 | Чему равны значения синуса, косинуса и тангенса для углов 300, 450, 600? |
| 30 | Сформулируйте выводы о взаимном расположении окружности прямой. |
| 31 | Какая прямая называется секущей по отношению к окружности? |
| 32 | Какая прямая называется касательной к окружности? Как называется общая точка прямой и окружности? |
| 33 | Сформулируйте и докажите теорему о свойстве касательной к окружности и обратную теорему. |
| 34 | Докажите утверждение об отрезках касательных к окружности, проведенных из одной точки. |
| 35 | Какой угол называется центральным углом? вписанным углом? |
| 36 | Как определяется градусная мера дуги? |
| 37 | Как определяется градусная мера центрального и вписанного угла? |
| 38 | Сформулируйте теоремы о четырех замечательных точках треугольника. |
| 39 | Какая окружность называется вписанной в многоугольник? описанной около многоугольника? |
| 40 | Какой многоугольник называется вписанным в окружность? описанным около окружности? |
| 41 | Сформулируйте теоремы о вписанной в треугольник и описанной около треугольника окружностях. |
| 42 | Каким свойством обладают стороны четырехугольника, описанного около окружности? вписанного в окружность? |






 дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ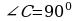 ,
, 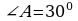 , АС = 10 см , СD
, АС = 10 см , СD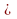 АВ, DE
АВ, DE 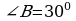 , ВС = 18 см , СК
, ВС = 18 см , СК 

 1) На рисунке АВ ║СД. А В
1) На рисунке АВ ║СД. А В Вариант – 2
Вариант – 2 1) На рисунке МN ║АС. MN
1) На рисунке МN ║АС. MN =90°, АС=8 см,
=90°, АС=8 см,  =45°. Найдите:
=45°. Найдите: С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и  =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.









