1 вариант.
1). Диагонали прямоугольника ABCD пересекается в точке О,  ABO = 36°. Найдите ABO = 36°. Найдите  AOD. AOD. 2). Найдите углы прямоугольной трапеции, если один из ее углов равен 20°. 3). Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма. 4). В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции. 5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, АМ = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.
| 2 вариант.
1). Диагонали прямоугольника MNKP пересекаются в точке О,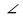 MON= 64°. Найдите MON= 64°. Найдите 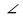 ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго. ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго. 3). Стороны параллелограмма относятся как 3 : 1, а его периметр равен 40 см. Найдите стороны параллелограмма. 4). В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции. 5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, длина диагонали АС равна 6 см. Найдите AM, если точка М лежит на продолжении стороны AD. |
1 вариант.
1). Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. 2). Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника. 3). Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. 4).* В прямоугольной трапеции АВСК большая боковая сторона равна 3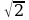 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции. см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.
| 2 вариант.
1). Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника. 2). Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и гипотенузу треугольника. 3). Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. 4).* В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции.
|
| 1 вариант.
1). По рис.  A = A =  B, СО = 4, DO = 6, АО = 5. B, СО = 4, DO = 6, АО = 5. Найти: а). ОВ; б). АС : BD; в).  . .
2 ). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треугольника MNK, если ). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треугольника MNK, если 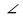 A = 80°, A = 80°, 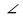 B = 60°. B = 60°. 3). Прямая пересекает стороны треугольника ABC в точках М и К соответственно так, что МК || АС, ВМ : АМ = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника ABC равен 25 см. 4). В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см2. | 2 вариант.
1). По рис. РЕ || NK, MP = 8, MN = 12, ME = 6. Найти: а) . МК; б). РЕ : NК; в). 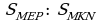 . . 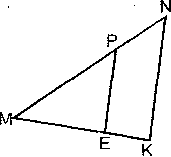
2). В ∆ АВС АВ = 12 см, ВС = 18 см, 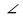 В = 70 0, а в ∆ МNК МN = 6 см, NК = 9 см, В = 70 0, а в ∆ МNК МN = 6 см, NК = 9 см, 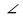 N = 70 0. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, N = 70 0. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, 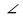 К = 60 0. К = 60 0. 3). Отрезки АВ и CD пересекаются в точке О так, что 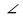 ACO = ACO = 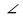 BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см. BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см. 4). В трапеции ABCD ( AD и ВС основания) диагонали пересекаются в точке О, 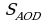 = 32 см2, = 32 см2, 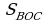 = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. |







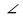 ABO = 36°. Найдите
ABO = 36°. Найдите 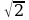 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.
см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции. .
. ). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треугольника MNK, если
). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треугольника MNK, если 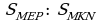 .
.
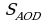 = 32 см2,
= 32 см2, 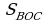 = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.
= 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.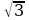 см. Найдите угол В и гипотенузу АВ.
см. Найдите угол В и гипотенузу АВ.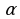 ,
, 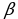 , сторона ВС = 7 см, ВН – высота. Найдите АН.
, сторона ВС = 7 см, ВН – высота. Найдите АН.
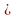 АВ :
АВ :