Конус и его сечения

Конус и его сечения

Определение.

Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называют образующими конуса (рис. 1). Образующие конуса равны.

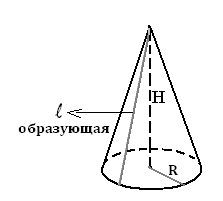
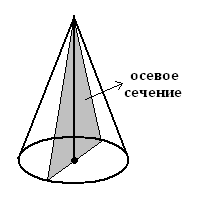
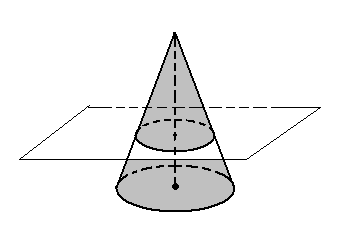
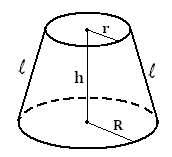
рис. 1 рис. 2 рис. 3 рис. 4 рис. 5

Радиусом конуса называется радиус его основания.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.

Сечения конуса

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением.

Осевое сечение конуса – равнобедренный треугольник, основание которого равно 2r, а боковые стороны – l (рис. 2)

Любое сечение конуса, проходящее через его вершину, представляет собой равнобедренный треугольник (рис. 3).

Сечение конуса плоскостью, параллельной основанию – круг, подобный основанию (рис. 4)

Плоскость, пересекающая конус параллельно его основанию, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом (рис. 5)

Площадь поверхности конуса

Боковая поверхность конуса составлена из образующих.

Полная поверхность конуса состоит из основания и боковой поверхности.

S_полн = S_осн + S_бок; S_осн = π ∙ r²; S_бок = πr ∙ l S_полн = π r ∙ (r +l)

S _осн = 0,25 d²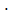_{ } π (через диаметр)

S _бок = 0,5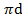_{ } l (через диаметр)

S _полн = 0,25 d²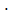_{ } π + 0,5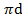_{ } l;

l²= h²+ 0,25 d²_{ }

r = 0,5_{ }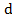

V=  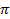_{   }r²h

Площадь поверхности усеченного конуса

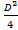S_полн = πl ( _{ } + _{ }) + π (_{ } + _{ }) (через диаметр)

S_полн = πl(R + r) + π (R² + r²)

S_бок = πl ( _{ } + _{ } ) (через диаметр)

S_бок = π l (R + r) , где l – образующая усеченного конуса, R – радиус нижнего основания, r – радиус верхнего основания.

Решите самостоятельно

№1. Образующая конуса равна 8 см, а радиус – 2 см. Найдите высоту и полную поверхность конуса.

№2. Найдите боковую поверхность конуса, диаметр основания которого равен 6 м, а высота – 4 м.

№3. Радиус основания конуса 3 м, высота 4 м. Найдите образующую конуса.