Тела вращения 11 класс Презентация к уроку Конус

Конус

Содержание

Зададим плоскость α и точку С вне этой плоскости. В плоскости α расположим окружность некоторого радиуса. Проведем прямые проходящие через точку С и все точки окружности. Поверхность, образованная отрезками с концами на окружности и в точке С образуют коническую поверхность .

С

Конус – это тело, ограниченное конической поверхностью и кругом, включая окружность.

α

Задание

Содержание

1) Приведите примеры из окружающего мира тел, похожих на тело полученное вращением треугольника вокруг оси, содержащей его сторону:

• Карликовое дерево

• Конусообраз-ные дома - трулли

Мороженное

Оградительные конусы

Кусты в королевском саду

Конусы - ракушки

Крыша-конус

Надувные конусы

Как Вы думаете, какова связь между этим телом и Как Вы думаете, какова связь между этим телом и этой картиной? этой картиной?

Как Вы думаете, какова связь между этим телом и этой картиной?

• Оказывается, самая непосредственная. Эта картина называется «Сосновый бор», её написал художник И.И.Шишкин. А тело, как Вы уже знаете, называется конус. Латинское слово konus позаимствовано из греческого языка («конос» - затычка, втулка, сосновая шишка).

Конус

Содержание

Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг оси, содержащей его катет.

• Круг – это основание конуса.

• Точка вне круга с которой соединяются все точки окружности – это вершина конуса.

• Прямая проходящая через центр круга и вершину конуса – есть ось конуса.

• Отрезок соединяющий вершину с любой точкой окружности основания – это образующая конуса.

• Радиус основания - это радиус конуса.

• Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.

Замечание: так как ось перпендикулярна основанию и проходит через вершину, то высота конуса лежит на его оси.

Конические сечения

Содержание

1) Если плоскость пересекает все образующие конической поверхности, то в сечении получается эллипс .

2) Если плоскость сечения параллельна одной из образующих, то в сечении получается парабола .

3) Если плоскость сечения пересекает обе полости конической поверхности, то в сечении получается гипербола .

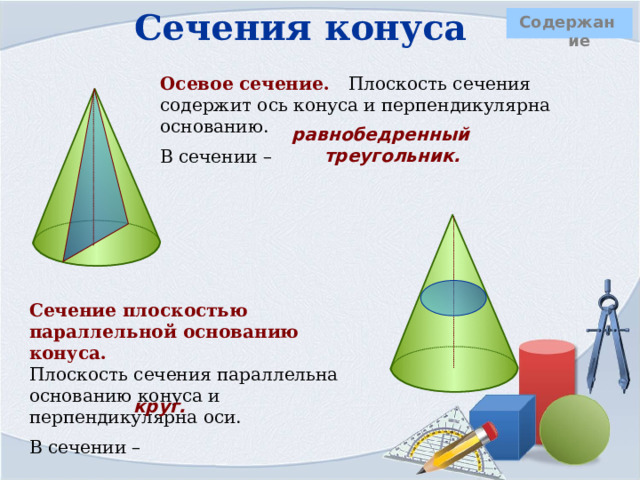
Сечения конуса

Содержание

Осевое сечение. Плоскость сечения содержит ось конуса и перпендикулярна основанию.

В сечении –

равнобедренный треугольник.

Сечение плоскостью параллельной основанию конуса. Плоскость сечения параллельна основанию конуса и перпендикулярна оси.

В сечении –

круг.

Площадь поверхности конуса

Содержание

Для вывода формулы площади полной поверхности конуса потребуется его развертка.

Полная поверхность состоит из основания и боковой поверхности.

Площадь основания находим как площадь круга

l

l

S =  R 2

R – радиус основания цилиндра

2  R

Боковая поверхность конуса есть …

R

R

сектор.

Площадь боковой поверхности вычисляется как площадь сектора радиус которого равен длине образующей конуса ( l ), а дуга равна длине окружности основания ( 2  R ). Площадь боковой поверхности конуса равна произведению радиуса на образующую и число  .

Получаем, S полн = S бок + S осн =  Rl +  R 2

S полн =  R(l + R)

Подробнее о площади сектора

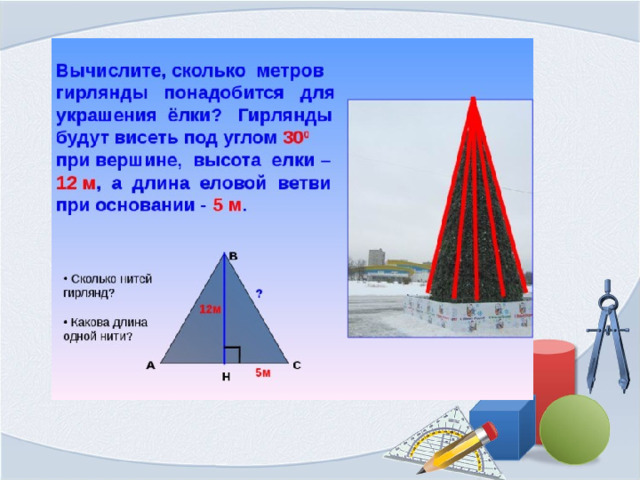
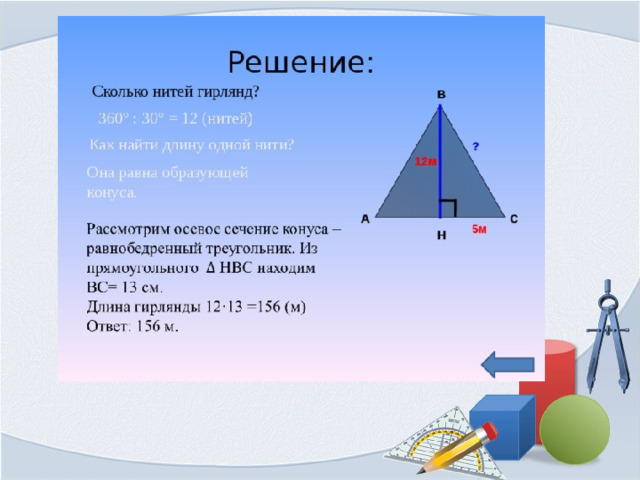
Решение устных задач с конусом

Содержание

1)Во сколько раз увеличится боковая поверхность конуса, если его образующая увеличится вдвое, а радиус основания одновременно увеличится в 3 раза?

2l

l

Ответ: площадь боковой поверхности увеличится в 6 раз.

R

3R

Sбок =  3R2l = 6  Rl

Sбок =  Rl

2) Вычислите площадь боковой и полной поверхностей конуса, длина образующей которого равна 10 см, а радиус основания 3 см.

Sосн =  R 2 =  · 3 2 = 9  (см 2 )

Sбок =  3·10 = 30  (см 2 )

10

Sполн = 39  (см 2 )

Ответ: 30  см 2 , 39  см 2

3

спасибо за внимание!

Благодарю

Литература

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для общеобразоват. учреждений. – М.: Просвещение, 2010.
• Бевз Г.П. и др. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
• Глейзер Г.Д. Геометрия: Учеб. пособие для 10-12 кл.веч. (смен.) шк. и самообразования. – М.: Просвещение, 1989.
• Клопский В.М., Скопец З.А., Ягодовский М.И. Геометрия: Учеб. пособие для 9 и 10 классов. – М.: Просвещение, 1980.

Интернет ресурс

• О географической широте
• Географические координаты
• Изображение сечений моделей цилиндра
• Изображение тел вращения
• Юла
• Волчок
• Игрушка
• Изображение тора
• Колокольчик
• Песочные часы
• Картинка для титульного слайда
• Паровой котел
• Рассеченный конус
• Картинка с сечениями
• Планета Земля
• Космический корабль